基于参数优化VMD的筒体故障识别

卢振东，张 云

(武汉理工大学 机电工程学院，湖北 武汉 430070)

回转窑是水泥生产“两磨一烧”中烧制的主要设备，其主要由驱动系统(大齿圈、小齿圈、电机传动系统)、支承系统(托轮及基座)、轮带和筒体等组成。筒体是物料反应进行的主要容器，在高温、重载运转时会出现温度分布不均匀、剧烈的热膨胀、雪球效应等现象，发生筒体热弯曲、轴线偏移等故障，直接影响水泥产量和质量。筒体表面温度区间在200～350 ℃，安装高度在4 m以上，直接对其测量有一定困难。筒体、轮带和托轮之间具有强耦合性，筒体的故障会反映在托轮上，引起托轮过载、振动及轴瓦过热等症状。托轮振动信号包含有反映筒体故障的信息，对其展开分析能有效地了解筒体运行状况，及时发现早期故障，减少企业经济损失，有重大的工程意义。

对于回转窑的故障诊断，已有大量的学者进行过研究。谷雨等[1]以回转窑主电机电流作为采集对象，运用小波包方法进行特征提取，结合神经网络技术实现故障分类识别。艾红等[2]学者重点探究了小波包变化在托轮轴故障诊断中的应用，结合实际数据，对内外圈故障状态下的数据进行处理，通过重构后信号功率谱峰值出现的位置对故障进行分类判断。张云等[3-4]采用经验模态分解(empirical mode decomposition,EMD)方法对回转窑振动信号进行了分析，实验效果良好。

变分模态分解(variational mode decomposition,VMD)是Dragomiretskiy等在2014年提出的一种将信号分解成有限数量但不同频段分量的方法[5]。该方法目前被广泛运用于机械故障诊断、金融学分析预测、地质学信号分析等领域。但是VMD方法存在模态数量K和惩罚因子α选取方法不明确，导致出现分解不足和模态混叠的问题。

1 变分模态分解

VMD算法将待处理信号分解为有限个不同频段的模态分量之和，如式(1)所示。

(1)

其中，每个分量uk(t)定义为调幅调频(AM-FM)信号，记为：

uk(t)=Ak(t)cos(φk(t))(k=1,2,…,K)

(2)

VMD算法通过Hilbert变换获得模态分量uk(t)的解析信号，并求取其正频谱，随后通过与当前中心频率估计的复指数混合而移位到基带，最后通过解析信号的H1平方范数来确定每个分量的带宽，构建了一个完全非递归的变分模态分解模型，其表达式如下：

(3)

为求解式(3)中{uk}和{ωk}两项的最优解，VMD算法引入二次惩罚项α和拉格朗日乘数λ对模型进行重建，将约束问题转化为非约束问题。二次惩罚因子α确保重构后数据不失真，另一方面，拉格朗日乘数λ代替执行原模型中的约束条件。为此，引入增广拉格朗日L，其定义如下：

L({uk},{ωk},λ)=

(4)

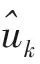
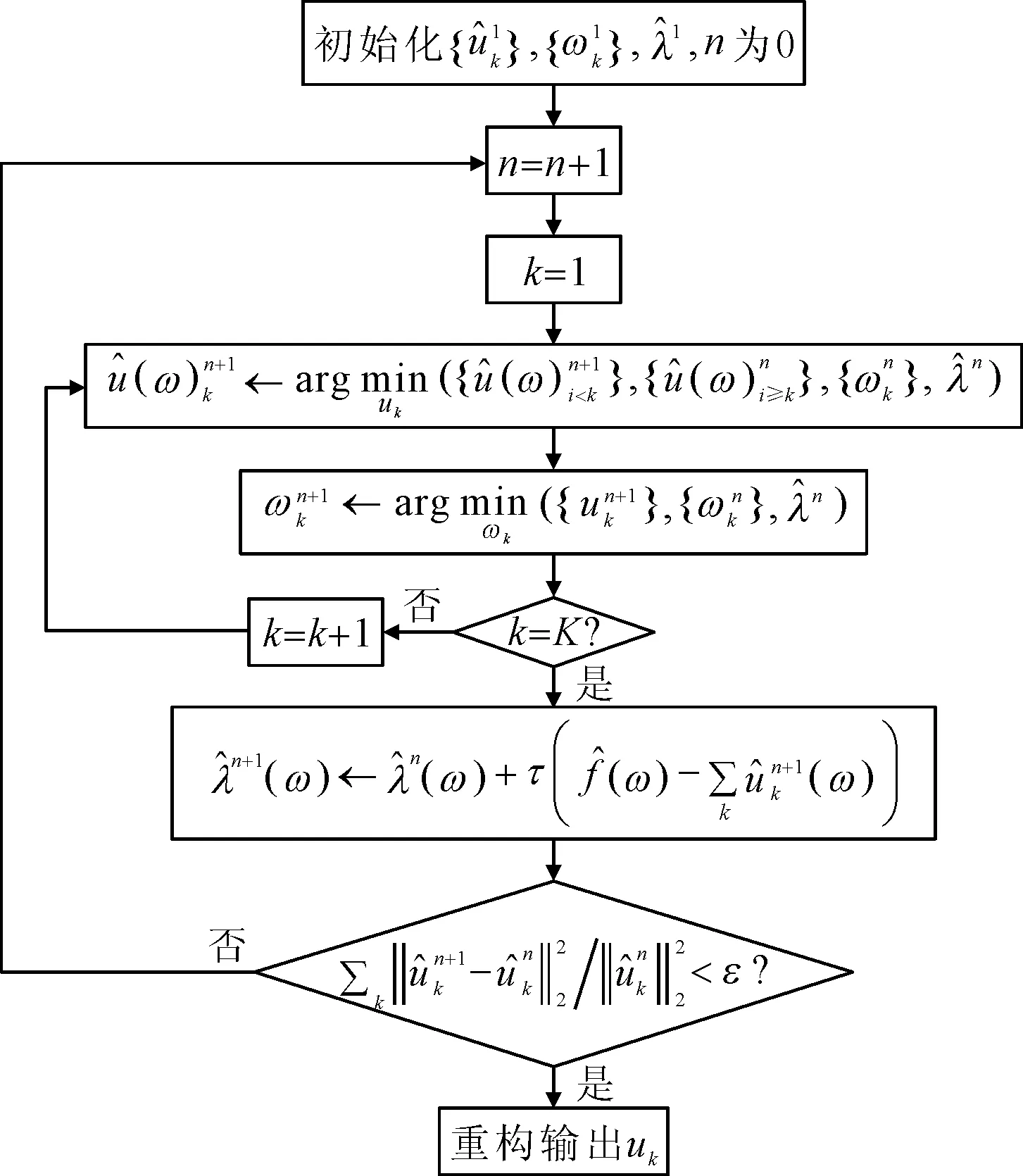
图1 优化ADMM求解流程图

2 参数优化VMD方法

2.1 模态数量K的选取

VMD方法中模态数量K为分解后的分量个数，K值过小会引起分解不完全，易出现模态混叠的现象，而K值过大则会出现虚假的模态分量，增加程序运行的时间。因此，引入能量的概念[6]来确定模态数量K的取值。

VMD方法将各分量定义为具有有限带宽的中心频率不同的信号，即分解所得的各分量具有良好的正交性，各分量相加能重构出原信号，因此完全分解后得到的各模态分量的能量之和与输入信号的能量应基本持平，以此可以作为确定分解后模态数量K的依据。现定义表征能量的参数如下：

(5)

式中：E为反映离散信号x(i)能量的参数；n为信号的长度。

为能良好表现不同K值下能量参数E的变化趋势，定义能量差参数ξ如下：

(6)

式中：Ef为输入信号f的能量参数值；Ek为第k个模态分量的能量参数值。

式(6)中，由于能量参数值E始终为正，能量差参数ξ的取值范围为0≤ξ<1(各模态分量完全正交时ξ=0)。当出现欠分解状况时，ξ取一个相对较大的数值；当分解较为完全时，ξ趋向于0。因此，能量差参数ξ可作为选取K值的参考。

2.2 惩罚因子α的选取

惩罚因子α是为解约束问题而引入的参数，主要用于确保重构后的数据不失真。α值会影响模态分量的带宽，取值越小，带宽越大，会引起模态混叠现象；取值越大，带宽越小，运算收敛速度越快，计算所需的时间越少，但是分量内包含的信息量也会减少[7]。惩罚因子α默认设定值为2 000，可以应对大多数分解状况，在部分情况下需要对α重新取值。笔者引入正交性指标IO来确定惩罚因子α的取值。

Huang等学者为了方便判别EMD分解后模态分量之间的正交状况所定义的正交性指标IO如下[8]：

(7)

式中：C(t)为模态分量；X(t)为原信号；T为信号长度。

正交性指标IO越大，各分量之间相关性越高，发生模态混叠的可能性越高；IO值越小说明各分量之间正交性越好，IO=0时，各分量之间完全正交。惩罚因子α取值越大，正交性指标IO越趋近于一个稳定的值，综合考虑模态带宽的情况下可以对α值进行选取。

2.3 参数优化VMD方法运算流程图

引入能量差参数ξ和正交性指标IO来选取模态数量K和惩罚因子α，经改进后的VMD方法运算流程如图2所示。虚线框a中，控制α=2 000，比较不同K值下参数ξ的绝对值及比值，确定K值。虚线框b中，控制K值不变，比较不同α值下正交性指标IO的比值，确定α的最佳值。

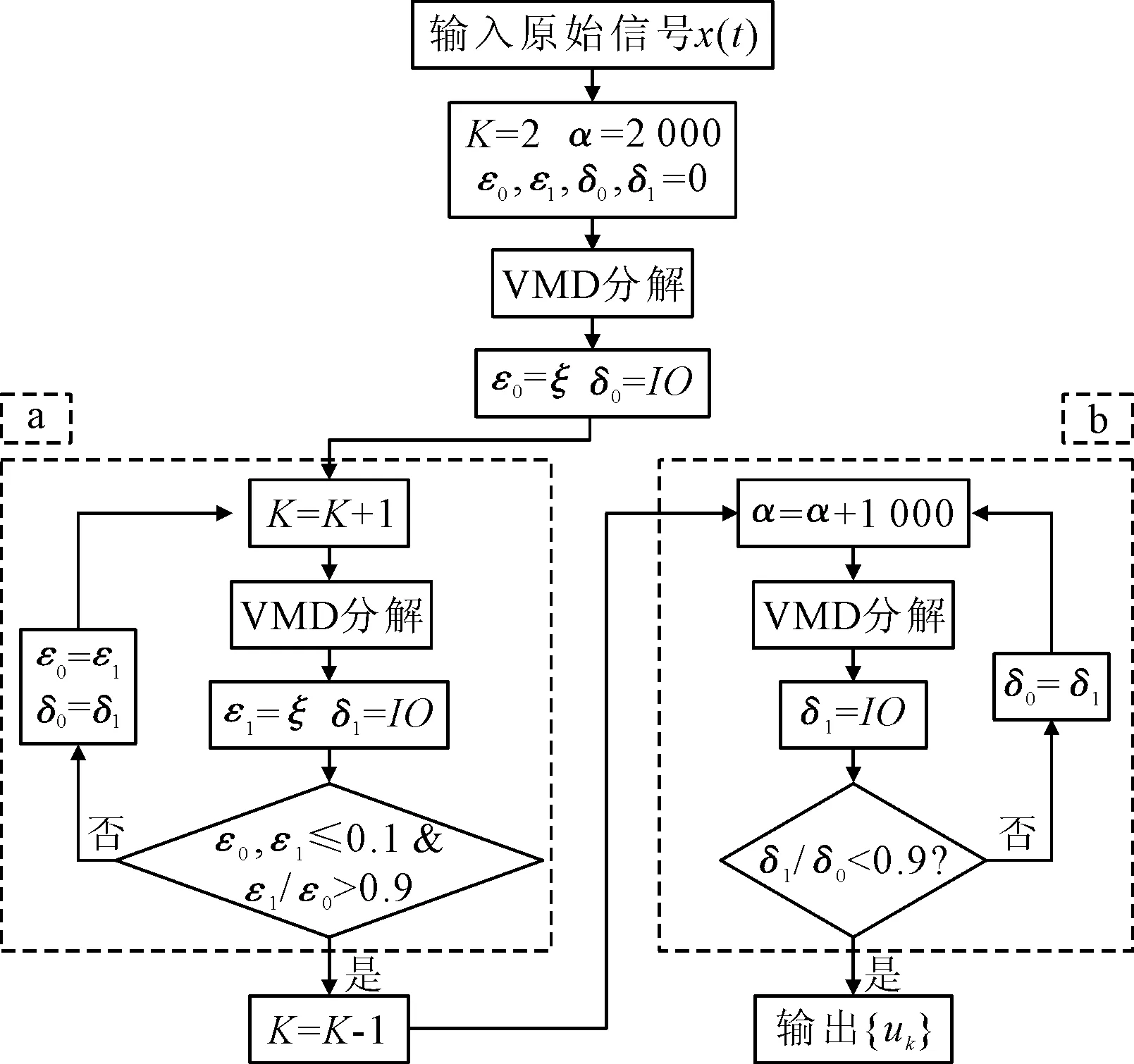
图2 参数优化VMD方法流程图

3 理论验证

3.1 仿真信号验证

构造仿真信号如下：

(8)

由于回转窑筒体运转周期为15 s左右，托轮周期约为筒体的1/3，回转窑系统属于低速旋转系统，频率低于1 Hz，故构造频率为0.06 Hz、0.2 Hz、0.6 Hz的3个信号相加，φ为正态分布的随机数作为噪声干扰信号。惩罚因子α取默认值2 000，采样点数为1 000，采样频率为3 Hz，输入信号如图3所示。

图3 仿真信号

选取不同模态数量K对信号进行VMD分解后，得到K与能量差参数ξ之间的关系如图4所示。从图4可知，当K为2、3时，ξ相对较大，此时出现了分解不足的情况；当K取到4或更大值时，ξ出现明显下降，并且比值曲线趋近于1，说明输入信号此时已完全分解，ξ随着K增大基本不变。此处，可以取K=4。

图4 α=2 000时能量差参数变化及比值曲线图

分别取K=3和4，α为默认值2 000对输入信号进行分解后得到的各模态分量及其频谱图如图5所示。

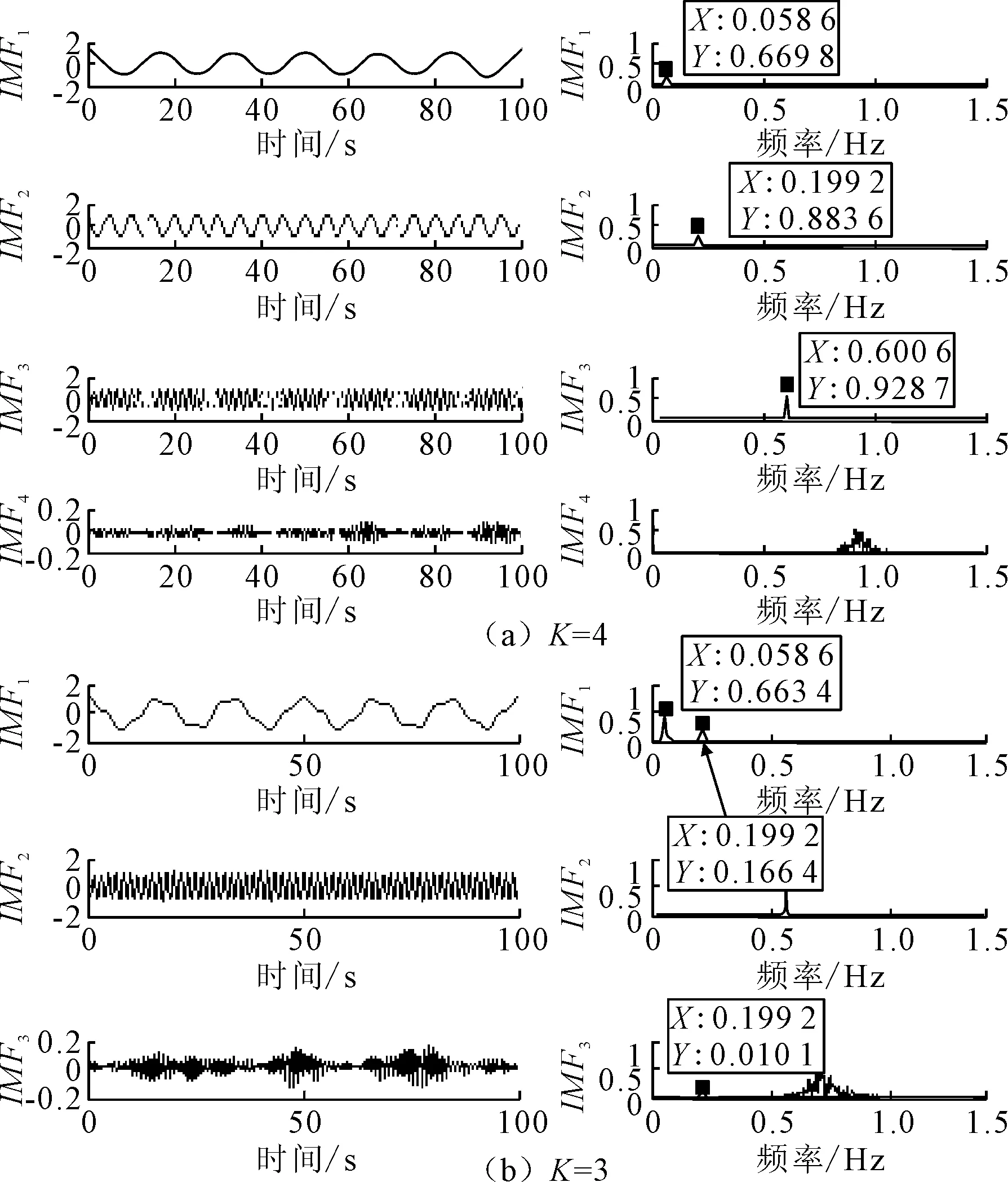
图5 模态分量时域图和频谱图

根据以上仿真结果，可以得出以下结论：

(1)K=4时，输入信号已完全分解，其中分量1、2、3分别为频率0.058 6 Hz、0.199 2 Hz以及0.600 6 Hz的信号，这与构造输入信号的3个信号的频率基本一致，说明VMD方法能从含噪声信号中分离频率相近的特征信号，证明了VMD方法用于低频信号分解的可行性；

(2)K=4时，各分量之间没有明显的模态混叠现象，而K=3时，频率为0.199 2 Hz的信号出现在分量1和分量3中，且较为微弱，出现了混叠及分解不足的情况，这与图4中曲线中ξ明显下降相吻合，证明通过能量差参数ξ来确定模态数量K这一方法的有效性。

3.2 实测数据验证

选用电涡流传感器、NI-6008采集卡及上位机，沿筒体与托轮中心连线方向，对四川省某窑托轮振动数据进行采集，如图6所示。

图6 托轮振动信号采集示意及现场图

以二档右托轮数据为例。筒体周期为16.5 s，采样频率为100 Hz，采集筒体旋转6圈时长的数据。采用参数优化VMD方法依次对K和α值进行选取，选取结果如图7和图8所示。

图7 α=2 000时能量差参数变化图

图8 K=7时正交性指标变化图

根据图7，选择K=7。从图8可知，当α小于77 000时，正交性指标趋于一个相对较大的值；当α在77 000～78 000之间时，出现了明显的下降；当α大于78 000后趋于稳定。保持K=7不变，分别取α=77 000和α=78 000进行分解，得到的部分分量如图9所示。

图9 部分模态分量时域图和频谱图

根据以上仿真结果，可以得出以下结论：当α=77 000时，频率为0.061 04 Hz和0.177 00 Hz的信号集中在1分量中，发生模态混叠现象；当α=78 000时，两个频率的信号被分离在1分量和5分量中，没有发生模态混叠。这一结果与图8中IO明显下降及比值曲线下凹区域相吻合，证明通过正交性指标IO来选取惩罚因子α这一方法的有效性。

4 基于参数优化VMD方法的筒体故障识别

提取模态分量中频率0.06 Hz和0.2 Hz左右的分量进行分析。由于能量参数E受信号长度n的影响较大，此处以能量的均值作为评价标准，其表达式如下：

(9)

式中：x(i)为输入信号；n为信号长度。

对四川某窑测量得到的托轮振动信号进行参数优化VMD分解，提取与筒体、托轮转频一致的特征信号求取能量均值如表1所示。

表1 特征信号能量均值 ×10-3mm2

对于筒体偏心故障，多采用激光传感器测量筒体轮廓，用最小二乘法拟合圆计算得到筒体截面偏心[9]，3个档位筒体偏心测量结果如表2所示。对于筒体中心线偏移多采用椭圆度测量方法，比较变形量曲线中经过左右托轮时局部的峰峰值R和L的大小关系，确定左右托轮受力情况[10]，3个档位左、右托轮变形量的局部峰峰值的比例关系如图10所示。下面将实际结果与能量均值结果进行对比分析。

表2 三个档位筒体偏心测量结果 mm

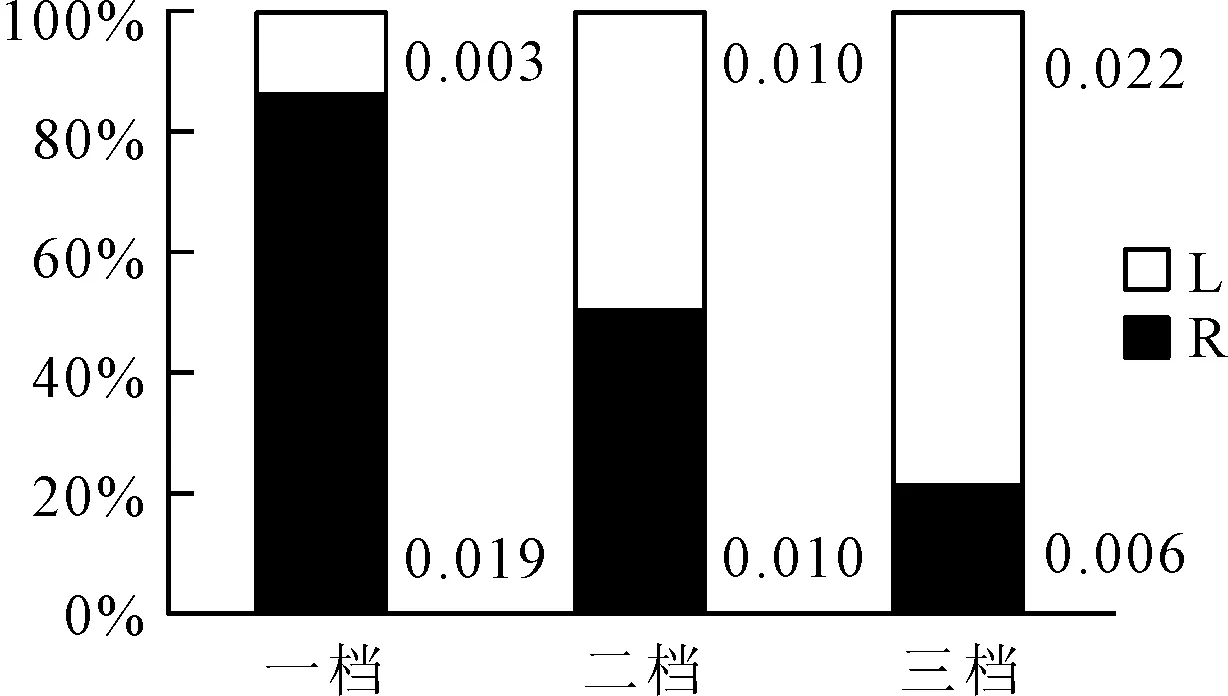
图10 托轮变形量的局部峰峰值R、L比例关系(变形量：mm)

图11为3个档位左右两侧的筒体信号能量均值，为方便比较，取两侧的平均值。二档数值最大，一档次之，三档最小，这一大小趋势与表2实际测量得到的3个档位的偏心情况一致。说明筒体特征信号能量均值能反映各个档位之间的偏心大小趋势，从而反映筒体偏心故障的严重程度。

图11 筒体特征信号能量均值图

图12为托轮特征信号能量均值比例关系。由图12可知，一档右侧托轮特征信号能量均值远远大于左侧，二档左右两侧基本相等，三档左侧数值大于右侧。对比图10和图12可知，图12中各档位左右两侧参数比例大小与图10中采用椭圆度测量结果相同。说明可以通过比较同一档位处两侧托轮特征信号的能量均值比例来反映托轮受力大小，从而判断筒体中心线水平偏移的情况。

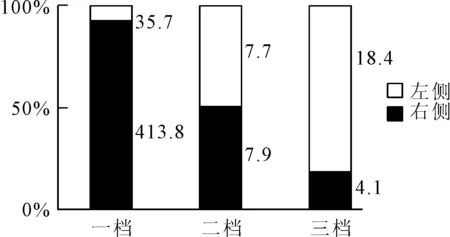
图12 托轮特征信号能量均值比例关系(能量均值：×10-3mm2)

5 结论

(1)所提出的参数优化VMD方法采用能量差参数ξ来选取模态数量K，用正交性指标IO来确定惩罚因子α，经仿真数据及实际数据验证有效，能有效避免分解过程中的模态混叠和分解不足状况，为VMD方法的参数选取提供了一条思路。

(2)引入参数优化VMD方法对托轮振动信号进行分解，提取带有能反映筒体偏心及水平偏移故障的信号，通过能量均值进行比较，与实际测量结果一致，证明参数优化VMD方法分解得到的特征信号能真实地反映筒体故障状况，为筒体故障识别提供了一种策略。