基于多刚体模型的某客车侧翻关键结构灵敏度分析

莫易敏，刘青春，高 烁，叶 畅，刘昌业

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.上汽通用五菱汽车股份有限公司，广西 柳州 545007)

客车在给人们生活提供便利的同时伴随着交通与安全问题，车辆交通事故直接对乘员造成身体和财产伤害的，在所有交通事故中，与正碰、侧碰相比侧翻所占比例小但乘员的死伤率非常高[1]。在侧翻事故中车体变形大，乘员生存空间侵入严重，导致乘员受伤害程度更严重[2]。因此侧翻关键结构灵敏度分析可为侧翻优化提供参考，对降低乘员伤害程度具有重要的社会意义。

由于对整车侧翻性能的影响规律研究需要大量数据支撑，若采取有限元模型进行仿真求解耗时过长，多次修改模型导致工作量巨大，无法获取大量仿真数据，而多刚体模型建模简单，计算时间远小于有限元模型，适用于研究侧翻关键结构的灵敏度。

运用Madymo软件建立客车多刚体模型，首先将整车模型划分为用铰链连接的有限个刚体构成的闭环系统，在有限元模型中提出主要部件的弯矩曲线特性并赋予多刚体模型铰链设置中，通过铰链刚度缩放系数改变铰链刚度从而改变各部件的抗弯强度。对侧翻关键结构A柱、B柱及顶盖横梁进行灵敏度分析，通过蒙特卡洛模拟进行响应估计，得到A柱贡献率最大。对关键结构进行灵敏度分析，在很大程度上为优化提供指导意见，提高优化效率，降低设计成本。

1 侧翻试验设计

1.1 试验台架

客车整车侧翻试验示意图如图1所示，车辆放置于举升角误差小于1°的翻转平台上，平台与地面高度差为800 mm，在试验车辆轮胎处设置侧向限位挡块防止在侧翻过程中车辆的侧向滑动，限位挡块的高度不得超过与之相邻轮胎的轮辋部位间距离的 2/3，挡块长度不得小于500 mm，宽度为20 mm，棱角半径为10 mm[3]。

试验过程如下：车辆放置于翻转平台，悬架锁止，车轮与翻转平台接触线为轴线，平台绕轴线缓慢旋转至车辆失稳临界位置，此时以初始角速度0.078 rad/s进行旋转，直到车辆翻转到地面。车辆在到达临界位置之前平台旋转不能产生晃动和动态效应，翻转角度速度不得超过5°/s(0.087 rad/s)[4-5]。其中图1中a、b、c点分别为客车在起始、临界以及触地瞬间的质心位置。

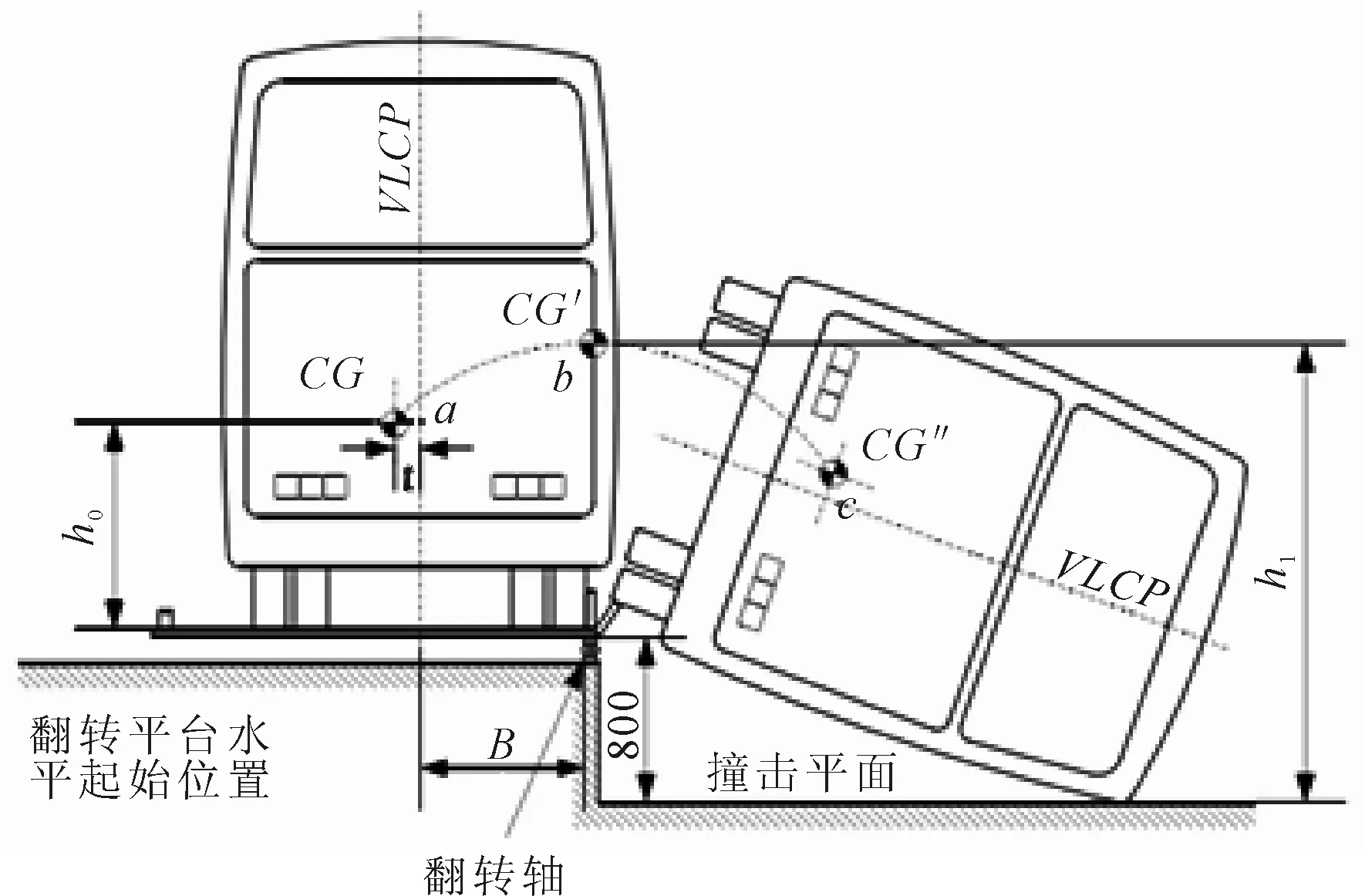
图1 客车整车侧翻试验示意图

1.2 生存空间设计

按GB/T 17578《客车上部结构强度》法规要求在SR点安装变形规，靠近侧围一侧涂有油漆。将长900 mm的测针一端平行于变形规表面且垂直边缘地穿过，另一端固定在车身上。通过比较试验前后暴露在变形规外面的测针长度获得最大侵入量，实现乘员生存空间的量化检测，同时根据车身内部是否沾有油漆判断生存空间是否被侵入[6]。生存空间示意图如图2所示。

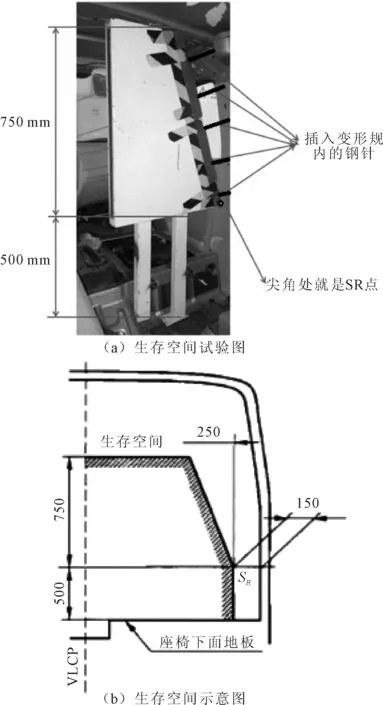
图2 生存空间示意图

2 侧翻仿真模型的建立与对标

2.1 有限元模型的建立

在UG中构建整车模型导出igs格式，在保证精度的前提下简化模型，利用Hypermesh进行网格划分。车辆产生变形部件为8 mm，生存空间为50 mm，其余为10 mm[7-8]。完成网格划分后，赋予整车材料及属性，定义部件间接触设置和连接关系，给整车设置的侧翻条件与试验保持一致。

2.2 试验与有限元仿真模型对标

试验与仿真结果表明在侧翻工况下，上部与侧围受挤压，生存空间被侵犯，其中B柱折弯，顶盖横梁侵入生存空间，随后A柱、B柱、C柱等侵入生存空间。如图3所示为试验与仿真整车模型以及部分结构侵入变形示意图，试验与有限元仿真仿真结果进行对比分析可知，有限元仿真模型精确，满足要求，可为关键结构灵敏度分析打下基础。

图3 结构变形对比

2.3 多刚体模型的建立

目前，在汽车被动安全研究领域中，多刚体动力学是模拟计算采用的主要方法之一[9]。多刚体动力学采用一些刚体和无质量的弹簧、阻尼以及各种动态铰链来描述系统的动态响应。车辆多刚体模型建立方法如下：

(1)车辆系统搭建。车辆由许多构件组成，多刚体仿真中可将各构件转化为刚体以简化研究，刚体间通过铰链连接构成多刚体系统。车身系统通过自由铰链与空间参考坐标系相连，确定车身原点与质心位置。

在Madymo软件中建立多体系统，将A、B、C、D柱、上边梁及顶部横梁等关键结构划分为有限个刚体，其中A柱均分为3段，B柱、C柱、D柱均分为两段，顶部横梁均分为4段，并用铰链连接各个刚体构成闭环系统。刚体的位置表示Madymo中Rigid坐标位置，铰链位置表示Madymo中Joint坐标位置，如图4(a)所示。根据在有限元模型中改变关键结构材料属性及厚度，获得不同的弯矩曲线，将不同的弯矩曲线特性赋予到多刚体模型中对应关键结构的铰链设置中。

图4 多刚体模型

(2)接触设置。接触参数设置的准确与否将直接影响仿真精度的高低。接触设置CONTACT.MB_MB反映了刚体自身材料特性及刚体间的接触特性。刚体间的接触力由摩擦力、阻尼力和弹力3部分组成，相应的设置参数为摩擦系数、阻尼系数、接触刚度曲线。由于不同部件间的接触特性不同，模型需被分为几组刚体组，来分别设置接触。将有限元模型中提取的关键部件的位置信息、质量信息、转动惯量、以及刚度特性相关参数等赋予到多刚体模型，得到多刚体模型，如图4(b)所示。

2.4 有限元模型与多刚体模型的对比验证

如图5所示，有限元模型与多刚体模型侧翻后整车变形大致相同，多刚体模型能较精确模拟有限元模型。

图5 有限元模型与多刚体模型的侧翻变形

3 关键结构分析

在进行灵敏度分析之前必须对侧翻主要结构进行分析，找到影响车辆侧翻耐撞性的关键结构。从最大侵入量、受力两个方面进行分析，以此来确定影响车辆侧翻中的关键结构。

3.1 最大侵入量

侧翻完成后整车最大侵入量为128.38 mm,试验与有限元仿真中关键结构最大侵入量如表1所示。整车在侧翻过程中生存空间受到侵入，车辆上部与侧围结构耐撞性有待提高。试验与仿真误差在5%以内，仿真模型满足工程要求。

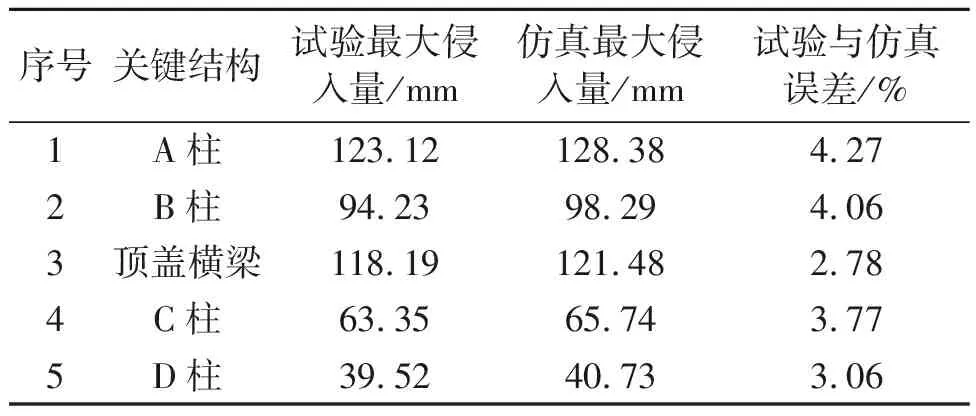
表1 试验与仿真的侵入量对比

3.2 碰撞力分析

通过Hyperview测得关键结构截面力。在侧面翻滚过程中，各个结构的截面力都在车身接触到地面的瞬间达到最大值59.35 kN，其中A柱、B柱、C柱和顶盖横梁的截面力最大值分别达到了22.4 kN、19.5 kN、11.1 kN和15.2 kN。

4 侧翻关键结构灵敏度分析

4.1 灵敏度分析基础理论

灵敏度分析能够快速找出各设计参数对系统的影响程度，保留对系统影响显著的设计参数。因此有必要对侧翻主要结构进行灵敏度分析，对侧翻关键结构优化提供方向，在很大程度上提高优化效率。从数学意义上灵敏度可以理解为：若函数F(X)可导，其一阶灵敏度可表示为[10]：

(1)

(2)

X=x1,x2,…,xj,…,xn

其中，式(1)为一阶微分灵敏度，式(2)为一阶差分灵敏度。

4.2 基于多刚体模型的关键结构灵敏度分析

要找出对侧翻变形量影响最大的部件，需要研究系统输出结果对参数变化的敏感程度。经过对关键结构分析，选取关键结构A柱、B柱及顶盖横梁的铰链刚度进行灵敏度分析。将A柱、B柱及顶盖横梁的铰链刚度缩放系数作为设计变量，通过最优拉丁方抽取15组仿真试验设计变量组合，并在Madymo软件中进行计算，得到Z向最大侵入量，具体抽样及最大侵入量部分数据如表2所示。

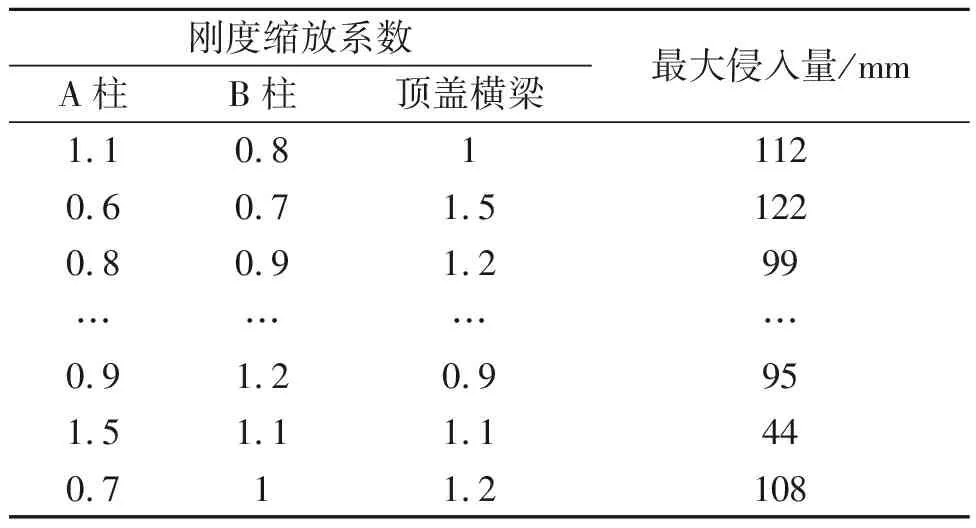
表2 设计变量抽样及其目标函数值

以最大侵入量作为输出响应，将A柱、B柱及顶盖横梁刚度缩放系数作为设计变量创建Kriging近似模型，通过蒙特卡洛模拟进行响应估计，缩放系数设计变量采样服从正态分布N(1，0.52)，在样本空间中用描述性采样方法抽取1 000个样本点，如图6(a)所示，其中坐标值代表对应结构的刚度缩放系数。完成各个设计变量的灵敏度分析，各设计变量对侧翻最大侵入量响应的贡献率分布如图6(b)所示，从图6中可以看出A柱明显对侧翻最大侵入量的贡献率最高。

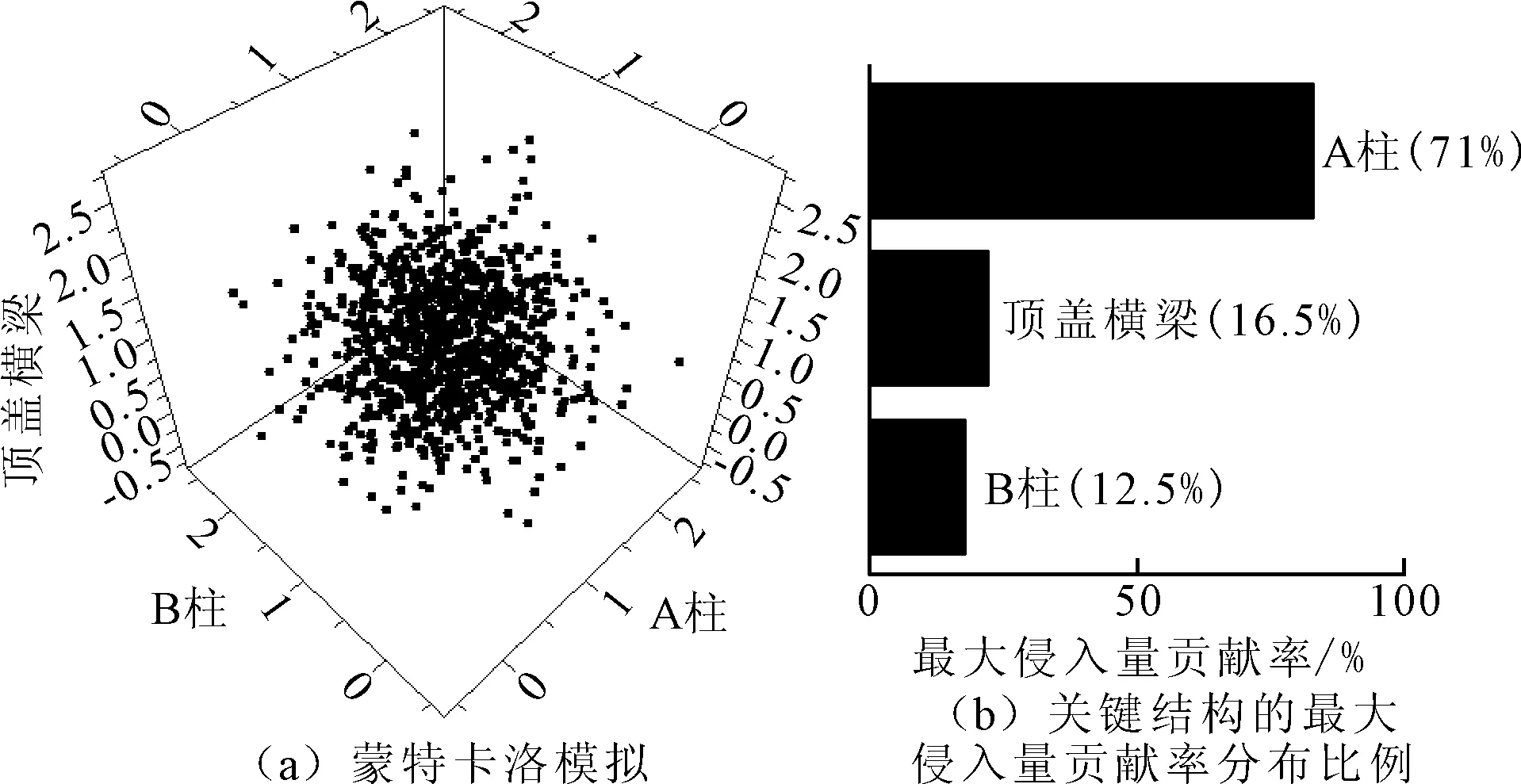
图6 关键结构灵敏度分析

5 结论

(1)在研究整车侧翻时，根据有限元模型对多刚体模型进行建模。通过改变有限元模型中关键结构的材料属性及厚度，提取不同弯矩曲线特性，赋予到多刚体模型对应结构的铰链中，通过Madymo软件计算，减小工作量，节省计算时间，大大提高效率。

(2)基于多刚体模型，将关键结构的铰链刚度缩放系数作为设计变量，运用蒙特卡洛模拟进行响应估计，对关键结构进行灵敏度分析，得到设计变量对最大侵入量的贡献率，在很大程度上降低了设计成本，提高优化效率。为其他车型确定侧翻关键结构提供了参考。