微电子器件重离子推导质子单粒子效应截面不同计算方法比较研究
2019-12-20张付强韩金华沈东军
张付强,韩金华,沈东军,郭 刚
(中国原子能科学研究院核物理研究所 国防科技工业抗辐照应用技术创新中心,北京 102413)
0 引言
宇宙辐射导致的单粒子效应(SEE)是微电子器件可靠性研究方向中的重要课题之一[1-2]。航天器搭载的各类微电子器件通常需要先在地面进行单粒子效应考核实验,再将考核实验结果结合空间轨道的辐射环境计算得到在轨错误率,以此作为依据,评判器件在实际应用中的可靠性。航天器在轨运行面临的宇宙辐射环境主要由超新星爆炸产生的重离子,太阳活动产生的质子,地球捕获带重离子、质子组成,因此目前以NASA及ESA为代表的发达国家及地区宇航组织指出,宇航用微电子器件单粒子效应考核需要评估器件在重离子和质子两种辐照条件下的响应。重离子单粒子效应的主要机理在于重离子入射后,其能量直接沉积于微电子器件的敏感区中,诱发电子空穴对的产生,使微电子器件的正常工作状态发生改变,通常器件的重离子单粒子效应采用σ-LET(Linear Energy Transfer)曲线进行描述,其中σ表示器件的单粒子效应截面,LET表示重离子在材料单位长度上沉积的能量。不同于重离子,质子单粒子效应的主要机理在于质子入射到器件后,与器件中的各种材料发生核反应产生次级粒子,而次级粒子在器件敏感区中进行能量沉积产生电子空穴对,导致器件正常工作状态的改变。质子单粒子效应截面采用σ-E曲线进行描述,其中σ为器件质子单粒子效应截面,E为质子的能量。可以认为重离子单粒子效应的机理属于质子单粒子效应机理的一个子集,由此为利用器件的重离子单粒子效应截面推算质子单粒子效应截面提供了理论基础。
由于微电子器件单粒子效应考核所用的粒子加速器设备庞大、收费昂贵、机时有限,使得针对器件同时开展重离子及质子的单粒子效应考核综合成本难以接受[3]。国内局限于质子单粒子效应实验装置的短缺,长期缺乏器件的质子单粒子效应实验结果,导致出现了器件重离子单粒子效应实验数据大量累积的情况。因此通过微电子器件的重离子单粒子效应数据推算质子单粒子效应数据显得非常重要[4-6],既能挖掘大量器件现有重离子单粒子效应实验数据的潜力,更能有效地指导后续质子单粒子效应实验的规范化和程序化。利用器件重离子单粒子效应数据推导计算质子单粒子效应的方法经过多年发展,已有BGR方法[7]、Petersen方法[8]、Barak方法[9]、PROFIT方法[10]以及Monte Carlo方法[11-12]等相继被报道。但是相关方法的适用范围和准确性还没有得到详细的对比和研究。
本文将基于已有的0.25μm CMOS工艺SRAM器件的重离子单粒子翻转截面数据开展常见的三种重离子推导质子单粒子翻转截面的方法比较研究,并与器件质子单粒子翻转截面实验数据进行比较,分析不同方法应用于器件空间错误率预估的适用范围和准确性。
1 计算过程
研究所用的0.25μm CMOS工艺SRAM器件重离子单粒子翻转截面数据[13]及质子单粒子翻转截面数据[14]通过Weibull拟合得到的关键参数如表1所列。将利用该器件的重离子单粒子翻转截面数据结合Bendel-Petersen方法、Barak方法及PROFIT方法开展对比研究。

表1 SRAM器件重离子及质子单粒子翻转截面数据Weibull拟合参数Tab.1 The parameter of the heavy ion SEU and proton induced SEU of the SRAM by Weibull matching
1.1 Bendel-Petersen方法
Bendel以及Petersen基于核反应理论提出了一种双参数模型方法用于重离子单粒子翻转截面计算质子单粒子翻转截面。

式中:σp为不同能量质子入射到器件中对应的单粒子翻转截面;σp(∞)为质子能量无穷大时入射到器件中对应的单粒子翻转截面,即器件的饱和截面;Y为一个与入射质子能量相关的量;σh为器件重离子单粒子翻转饱和截面;L0.25为器件重离子单粒子翻转饱和截面1/4值位置对应的LET值。

器件质子单粒子翻转阈值与重离子单粒子翻转阈值关系可由式(4)表示:

式中:L0为器件的重离子单粒子翻转截面阈值;A为器件的质子单粒子翻转截面阈值。
将器件的重离子单粒子翻转截面数据代入上述公式,可以推算得到器件的质子单粒子翻转截面,如图1所示。

图1 用不同方法得到的质子单粒子翻转截面曲线与试验测试结果对比图Fig.1 The proton induced SEU curve by different method compare with experiment result
1.2 Barak方法
Barak等[9]利用不同能量质子入射到表面势垒探测器得到的质子-硅核反应次级粒子能谱,结合灵敏区体积模型及阶跃函数对积分公式进行简化,提出了一种简单的由器件重离子单粒子翻转截面推算质子单粒子翻转截面的方法:

式中:Ep为入射质子能量;σp(Ep)为质子能量为Ep时对应的单粒子翻转截面;σHI∞为器件重离子单粒子效应中入射粒子LET值无穷大时对应的器件重离子单粒子翻转截面,即饱和截面。P(Ep,Lc)是能量为EP的质子入射到器件灵敏区产生LET值为Lc的次级粒子的概率。

式(6)基于器件质子单粒子翻转Weibull函数,可以简化为阶跃函数。在该阶跃函数中,横坐标为入射重离子的LET值,纵坐标(翻转截面)则从0阶跃至σHI∞,其中Lc对应阶跃函数阶跃点的横坐标;L0为器件重离子单粒子翻转截面阈值;S和W分别为器件重离子单粒子翻转截面采用Weibull拟合得到的关键参数。

由式(5)~(7)结合器件重离子相关数据计算得到的器件的质子单粒子翻转截面数据如图1所示。
1.3 PROFIT方法
Calvel等[10]将质子-硅核反应简化为弹性碰撞提出了一种经验公式,用于从器件的重离子单粒子翻转截面计算质子单粒子翻转截面,被称为PROFIT方法:

式中:Ep为质子能量;Σp(Ep)为质子能量为Ep时对应的质子单粒子翻转截面;Σ0、L0、S、W分别是由器件重离子单粒子翻转饱和截面Weibull拟合得到的关键参数;h为器件的耗尽层厚度;Nat=5×1022为硅原子核密度。L(E)用于描述硅原子核在硅材料中的电子阻止本领,可以用式(9)表示。∑nuc(Ep)用于描述质子-硅核反应的截面,在质子能量1~1 000 MeV范围时,可以用式(10)进行描述。

式中:a=-0.15;b=1.04;c=3.1;d=3.9×10-3;e=3.106×10-3,均为无量纲量。
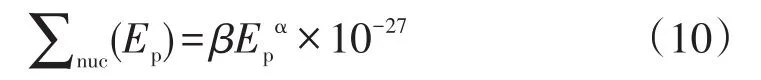
式中:α=-0.5;β=758.95,为无量纲常数。
式(8)中质子与硅原子核发生弹性碰撞产生的反冲硅核能量ESi(T)可以用核反应理论中弹性碰撞式(11)进行表述,也可以利用Monte Carlo方法计算得到。

式中:ASi为硅原子核的质量;T为入射质子弹性碰撞后的平均散射角;Ep为入射质子的能量。
本研究通过利用Monte Carlo模拟,计算得到了不同能量质子与硅原子核发生弹性碰撞后的反冲硅核能量,如表2所列。

表2 不同能量质子与硅原子核弹性碰撞产生的反冲硅核能量Tab.2 The energy of the recoil Si atoms by proton-silicon elastic interaction
通过计算发现,对于本款器件在不同能量质子条件下得到的L(ESi(Ep))<L0,由此无法得到有效的Σp(Ep)。计算结果表明,PROFIT方法有着其适用范围:如果器件的重离子单粒子翻转阈值较高,则该方法并不适用。其物理内涵在于,如果质子-硅核反应产生的反冲硅核在硅材料中的LET值小于器件的重离子单粒子翻转阈值,则无法触发翻转。该方法将质子-硅核反应简化为弹性碰撞,并将反冲硅核作为主要次级粒子的代表,是一种较为粗略的近似。
2 分析与讨论
图1为用经验公式计算得到的器件质子单粒子翻转截面数据,通过式(12)进行Weibull拟合得到的截面曲线相关参数如表3所列。Weibull拟合是单粒子效应研究领域一种常见的数据拟合方法,主要由四个参数构成,其中A代表器件的单粒子效应饱和截面值,L0代表器件单粒子翻转阈值,W是宽度参数,S是无量纲指数。同时,通过Weibull拟合得到的四个参数值恰好是单粒子效应空间错误率预估研究领域最常用软件之一Space Radiation软件计算单粒子空间错误率的输入值。


表3 用不同计算方法得到的器件质子单粒子翻转截面曲线Weibull拟合参数表Tab.3 The parameter of the proton induced SEU curve by different method
整体来看,Barak方法和Bendel-Petersen方法计算得到的器件质子单粒子翻转截面曲线趋势与实验测得曲线较为一致,单粒子翻转阈值与测量值较为一致,但是饱和翻转截面值与测量值存在数量级的差异。分别来看,Barak方法适用性更为广泛,能够计算低能到高能所有能量段质子对应的单粒子翻转截面,Bendel-Petersen方法只能计算中高能量段质子对应的翻转截面。主要原因在于,用Bendel-Petersen方法计算得到的器件质子单粒子翻转阈值A与器件重离子单粒子翻转阈值L0存在强相关关系,Bendel-Petersen方法对于高重离子翻转阈值的器件是不适用的。
由此可以认为,Barak方法适用性最为广泛,计算得到的器件质子单粒子翻转阈值较为准确。Bendel-Petersen方法适用性一般,器件重离子单粒子效应截面阈值的大小将对其适用范围存在一定影响。PROFIT方法适用性较窄,器件重离子单粒子效应截面阈值的大小对其适用范围存在较大影响。当然,随着微电子行业的不断发展,金属布线层、金属通孔等技术广泛应用于现代微电子器件上。金属材料的引入,尤其是重金属材料与质子核反应的次级粒子最大LET值显著高于与硅材料核反应后的次级粒子LET值[15],可能会导致器件可能对单粒子效应更加敏感,单粒子翻转的阈值将会降低。这些现象的出现将对Bendel-Petersen方法和PROFIT方法的适用范围有一定程度的拓宽。
为进一步分析不同质子单粒子效应截面计算方法的特点,还利用Space Radiation 7.0软件预估了用不同方法得到的器件应用于卫星典型轨道的空间错误率,计算结果如表4所列。
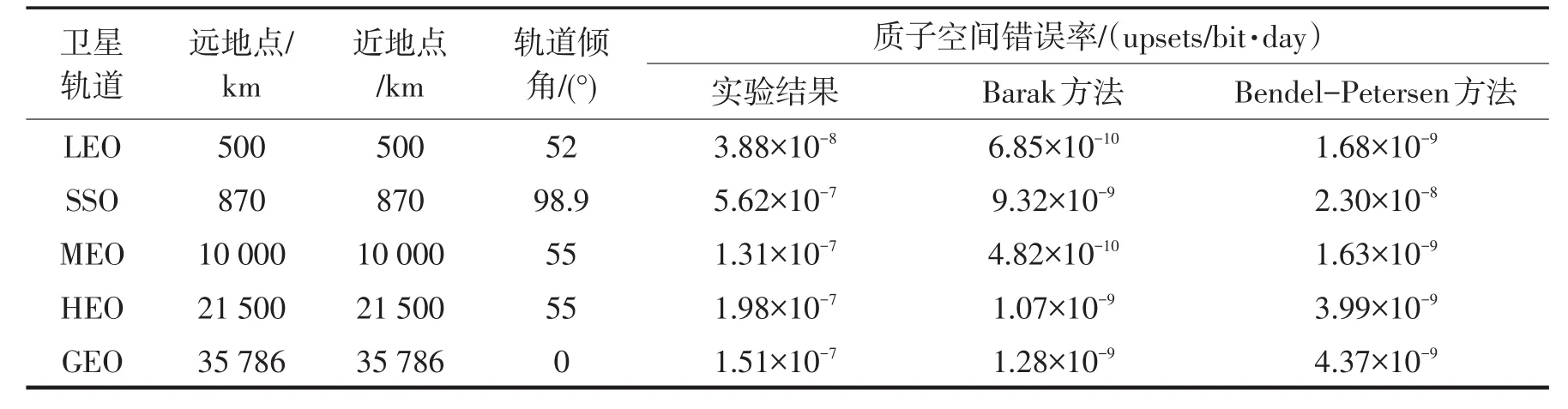
表4 用不同计算方法得到的器件典型轨道在轨运行质子空间错误率Tab.4 Proton Induced on orbit soft error rate by different method
在计算过程中选取地磁场屏蔽为平静,地球捕获带质子为AP-8模型,太阳活动质子为JPL1991模型,航天器屏蔽环境为3 mm等效铝厚度。从表中可以看到,用Barak方法和Bendel-Petersen方法计算得到的器件空间错误率与实验结果相比均出现了数量级的差异。Barak方法得到的结果比Bendel-Petersen方法误差更大,其主要原因在于,用Barak方法得到的器件质子单粒子翻转饱和截面数据相比于实验测量所得数据误差更大,最终反映在器件的典型轨道在轨错误率中。
3 总结
本研究利用0.25μm CMOS工艺SRAM器件的重离子及质子单粒子翻转实验截面数据,分析了Barak,Bendel-Petersen以及PROFIT三种常见的由器件重离子单粒子翻转数据推导质子单粒子翻转数据的方法,并利用Space Radiation空间错误率预估软件计算了不同方法得到的器件搭载于典型卫星轨道的空间错误率。研究表明,在适用性方面Barak方法最为广泛,Bendel-Petersen和PROFIT方法的适用性与器件的重离子单粒子翻转阈值呈负相关性,器件重离子单粒子翻转阈值越高,这两种方法的适用性越窄。在计算得到的质子单粒子翻转截面数据准确性方面,Bendel-Petersen方法准确性最好,Barak方法次之。该研究将有助于研究者更有针对性的选择器件重离子推导质子单粒子效应数据的方法,提高计算的效率和准确性。
