穿脉数据约束下的金属矿体三维建模

刘亚静，谭 政，李 梅，杜映东

(1.华北理工大学矿业工程学院，河北 唐山 063210； 2.北京大学地球与空间科学学院，北京 100871； 3.内蒙古自治区矿产实验研究所，内蒙古 呼和浩特 010000)

对金属矿体三维模型的精确构建是数字矿山建设过程的一个重要环节，是进行储量估算的重要方法。三维矿体模型包括矿体表面模型和矿体内部体元模型[1-3]，矿体内部体元模型通过插值计算确定了矿体的储量精度，而矿体表面模型的精确勾勒决定了矿体形态的精确度[4-5]。目前矿体表模型的建模方式主要以平行轮廓线建模为主，通过两轮廓线上的点构建一系列三角形面片来表示矿体形态[6]。但若两轮廓线不平行，则在建模过程中会导致模型出错。为了能尽可能提高矿体表面模型的准确性，许多学者在该方面进行了相关研究。唐丙寅等[7]在分析传统由矿体表面模型约束矿体实体模型建模方法存在的速度、效率问题后，提出在钻孔数量充足的情况下利用钻孔中提取的地质体各层数据点，通过点、线、面、体的递进式地质建模方法，实现了利用单一数据源高精度建模。朱良峰等[8]在考虑地质约束作用及地质学原理的耦合关系，用边界模型与地质晶胞模型构建混合数据模型。以区域面积重合判断法为基础，结合加权品位重心曲线和轮廓线缩放系数两个参数，从局部和整体两个层面解决了轮廓线的对应计算问题。曹国林等[9]讨论了复杂轮廓线下的镶嵌和分支问题，并给出了基于通过添加控制线和辅助分支信息的解决算法。罗智勇等[10]、郭艳军等[11]提出引用各种物探资料形成交叉折剖面对钻孔数据进行约束以控制诸如尖灭、棱镜体等特殊地质体特征。李兆亮等[12]、杨洋等[13]提出的构建轮廓线映射函数来优化矿体表面。这些研究成果重点在于实现复杂矿体表面模型的建立，没有考虑矿体模型的还原程度，且其建模所用数据源以钻孔数据为主，模型精度极大地依赖于勘探的钻孔数据量，这就需要由充足的钻孔数据作为建模支撑。然而在实际开采中却因实际操作原因可能出现钻孔开采不规范、钻孔数据不足的问题，致使三维模型建模精度降低，影响对矿山储量的估算。基于此问题，本文提出利用开采过程中的穿脉数据作为轮廓线建模辅助数据约束矿体表面形态，并提出约束建模算法来提高建模精度，以更准确地估算矿山储量。内蒙古油篓沟矿区现在对1650、1690、1730三个中段进行开采，本研究以这三个中段开采过程中的穿脉数据进行模型构建。

1 矿体表面模型建模算法

1.1 传统平行轮廓线建模方式

传统平行轮廓线建模方式的实质是有向图的最优路径搜索算法。该方法将每条轮廓线上的点作为一个点集，相邻两轮廓线上的点集合构成了搜索图矩阵，并按一定方向进行点搜索，依次选取接下来两路径中较短路径作为最优路径进行计算。因此首先需要将勘探线进行点离散，并重新组织勘探线上点的点序。采用逆序对轮廓线上的点进行编号，使得编码顺序一致。然后确定两轮廓线的起始搜索点，并搜索两轮廓线的下一点，判断出两点与下一点交叉形成边中的最短边，并由此构成三角形面片。

如图1所示，设相邻两勘探线为A、B，设A的起始点号为A_i，遍历B上的点，直至找到B_j，令A_iB_j的距离为最短，则设B_j为B的起始搜索点，A_iB_j为起始搜索边，并对A、B两线上点进行逆时针走向重新排序。以A_i和B_j为起点边，分别确定A_iB_(j+1)和A_(i+1)B_j的长度，比较得到最短边两点为新的起始点，且存储该边与起始边构成三角面片。

图1 最短对角线轮廓连接示意图Fig.1 Sketch map of the shortest diagonalcontour connection

但是当空间中两轮廓线的形态、倾斜角、中心位置等存在较大偏差的情况时，该方法将会出现某一轮廓线上的全部点连接至另一轮廓线上个别点的问题，如图2所示，在实际建模中，图2中两轮廓线中间的横向线段(轮廓线A和轮廓线B线段)表示的是两轮廓线的连接线，任意两条连接线与其在轮廓线上对应的线段构成三角形面片，两轮廓线上所有的三角形面片构成该部分矿体的外表面。当两轮廓线在形态、倾斜角以及中心位置偏差不大的情况下，可以顺利完成表面拟合，如图2中最左端的轮廓线A和其右端的轮廓线B用平行轮廓线方法连结成矿体表面。但是由于轮廓线B和其右端的轮廓线C倾角存在较大偏差，所以依靠平行轮廓线寻找最短边的搜索建模方式会产生如图2所示的问题，轮廓线B上的点全部连接至轮廓线C上的某一点，因此无法依靠形成的一系列三角形面作为矿体表面模型。

1.2 穿脉数据约束下的矿体表面三维建模

穿脉数据约束下的矿体表面建模方法是在传统平行轮廓现建模方式的基础上，加入穿脉数据进行改进，重点在于穿脉数据对矿体轮廓线数据的匹配和约束问题。

1.2.1 穿脉数据与矿体轮廓线图匹配

在某水平中段进行穿脉掘进所得到的穿脉数据往往不与任意矿体轮廓线共面，因此在穿脉数据与矿体轮廓线进行联合建模时需要考虑穿脉数据与轮廓线数据的匹配问题。如图3(a)所示，穿脉A(CM_A)和穿脉B(CM_B)代表某一开采中段上的两条相邻穿脉，而穿脉线上的点P_CM_A和P_CM_B分别代表了穿脉线上最外端的见矿段点，两见矿点也代表矿体外表面上的点。若直接连接两点，如图3(a)中的虚线，并不与轮廓线B(LKXB)相交。

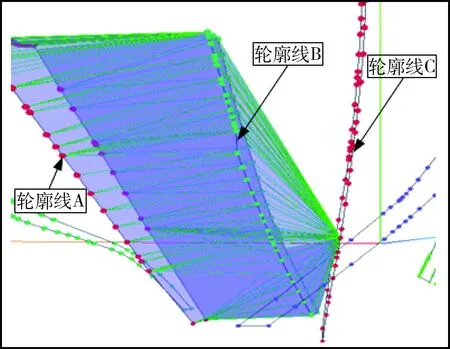
图2 轮廓线连接问题图Fig.2 Contour connection problem diagram

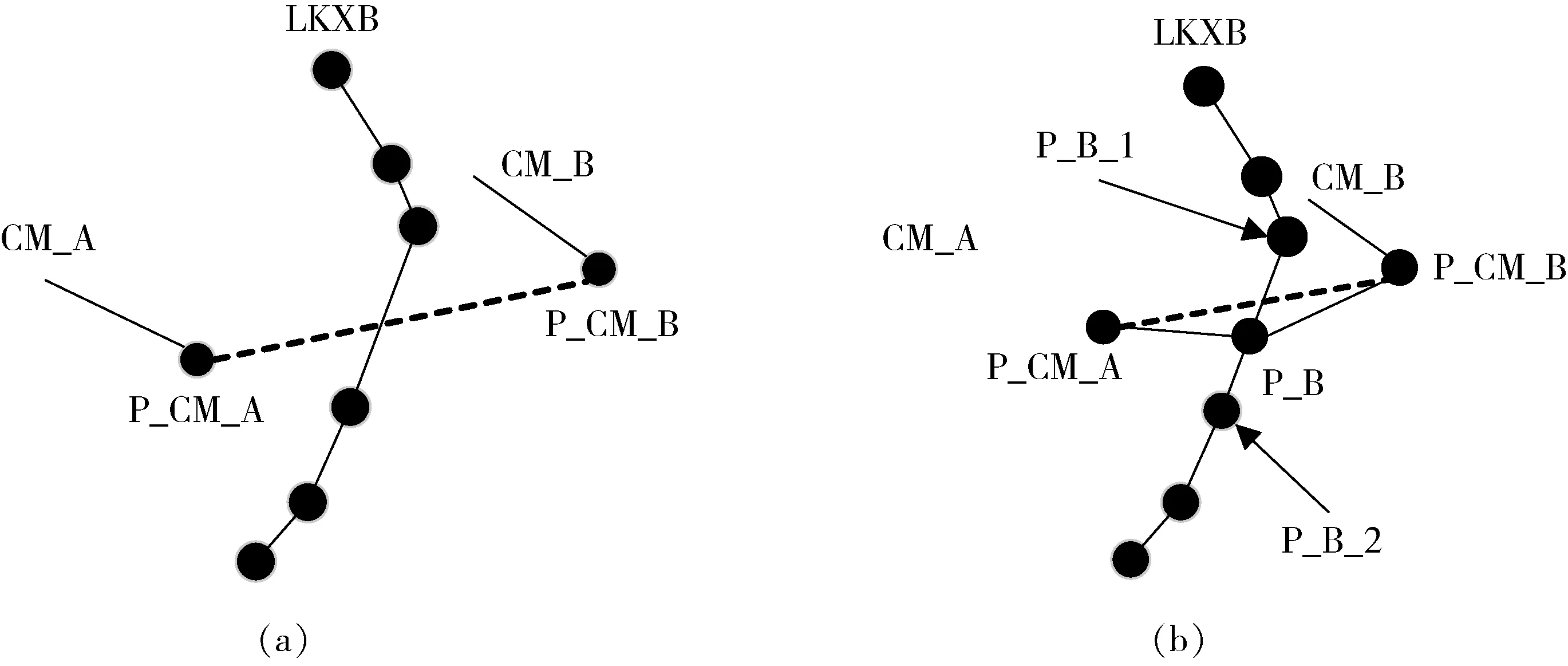
图3 轮廓线与穿脉数据匹配图Fig.3 Diagram of contour match with transverse drift data

因此需要在LKXB中找到一个位于穿脉所在平面的点P_B，将该点与P_CM_A和P_CM_B相连，得到约束矿体表面的控制线。如图3(b)所示，这便将问题转换成为已知空间平面求某一线与该平面的相交点坐标问题。但是通过观察图可知，可用更为简单的通过求在某一高程坐标下的某空间直线的x，y坐标来求解。通过遍历轮廓线坐标点值，找到最接近某一开采中段高程的两点，这两点坐标要求其中一点高程要大于中段高程，另一点要低于中段高程，如图3中所示P_B_1和P_B_2。则可通过这两点的空间坐标按照空间直线方程确定，见式(1)。

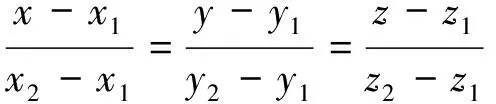
(1)

由于已知中段高程z，则可求出P_B对应x、y坐标。最终连接P_CM_A与P_B与P_CM_B则可构建控制线。由于内蒙古油篓沟矿区开采分1650、1690、1730三个中段，因此可以通过三个中段中的穿脉数据形成一个三层的矿体表面约束。

1.2.2 穿脉数据约束下建模

由1.2.1节算法可以得到各轮廓线分别与三个中段平面的交点，以及该点到相邻两穿脉线上见矿点的线性方程f1和f2。因每个中段的穿脉开凿与矿体的分布有关，因此任意相邻两中段的穿脉不是一一对应的，各中段所开凿的穿脉条数不一致，无法以简单的线性关系来表示两穿脉关系。如图4所示，1690中段采掘穿脉CM_A和CM_B，最外端见矿点为实心圆，1650中段穿脉CM_C和CM_D，最外端见矿点为实心方形。若仅用直线连接1690中段穿脉B(CM_B)上的点P_CM_B和1650中段穿脉D(CM_D)上点P_CM_D，并不能很好体现矿体表面的曲折性，且在实际操作中也很难找到具有对应关系的CM_B和CM_D。

因此，设计将在进行1.2.1节进行P_CM_A、P_B和P_CM_B三点的空间直线运算的同时，记录P_B点与P_CM_A和P_CM_B的两直线方程，并遍历中段1650与1690中段之间的各点，分别将轮廓线上点带入f1和f2进行计算，得到由穿脉数据和中段切分的约束轮廓线。设LKXB与1690平面相交点P_B与其逆时针方向邻近的点P_CM_B构成的空间直线方程为f1,LKXD与1650中段平面相交点P_D与其逆时针方向临近点P_CM_D构成的空间直线方程为f2。

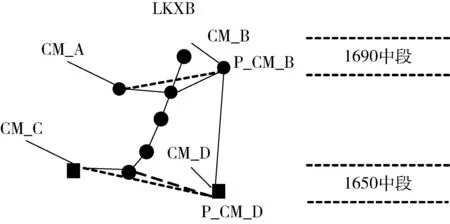
图4 两中段穿脉数据连接示意图Fig.4 Diagram of data connection of two mid-sectionpulse-piercing

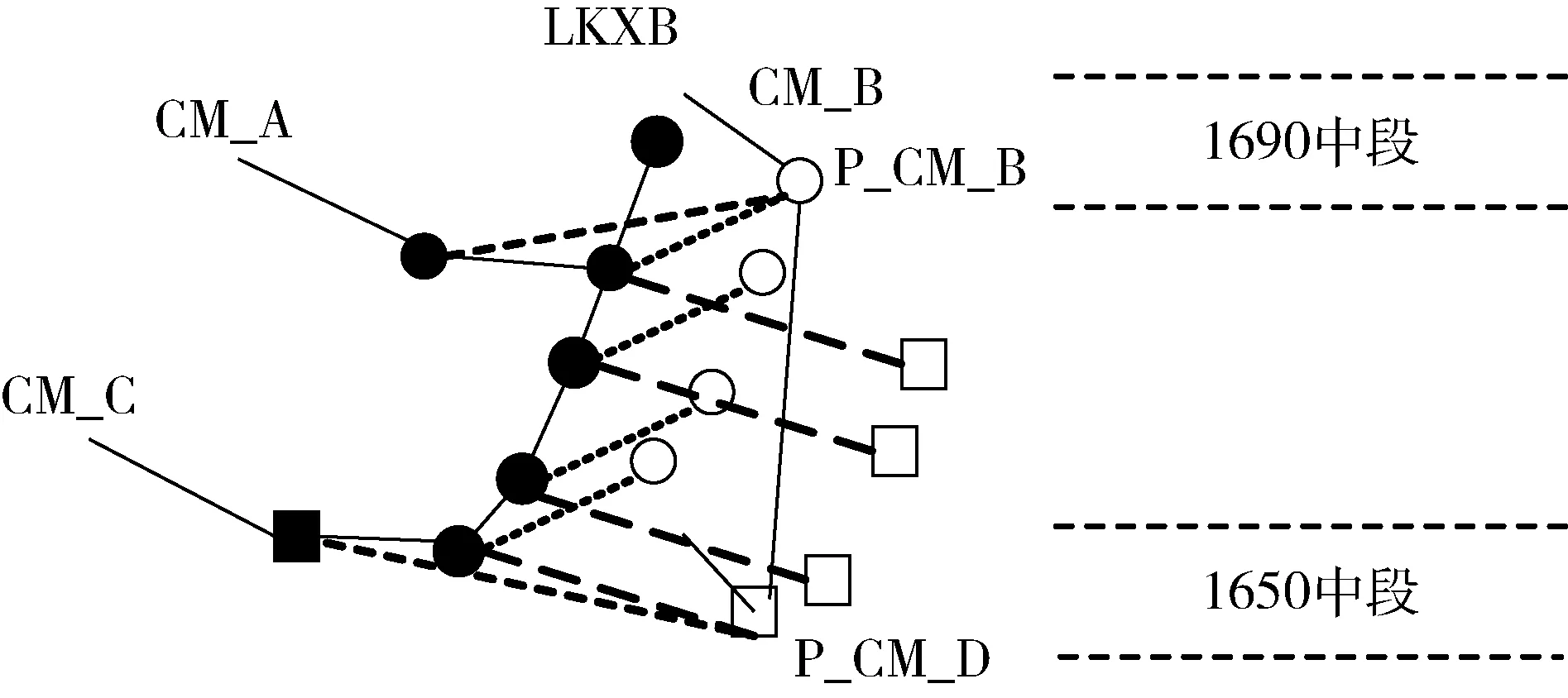
图5 穿脉约束矿体表面算法过程示意图Fig.5 Schematic diagram of algorithm process fortransverse drift constrained orebody surface

如图5所示，先由1690中段处点向下遍历，实心圆P_CM_B是1690中段穿脉B上的见矿点，点状虚线代表空间直线方程f1，空心圆代表LKXB上的点经过f1运算后产生的约束轮廓线上的点。然后再由1650中段向上遍历，实心方形是11650中段穿脉B上的见矿点，长虚线代表空间直线方程f2,则空心方形代表新生成的约束线上的点。以此类推，在两种段间同一轮廓线上的点进行向上向下两次遍历，分别带入函数式f1和f2，则可生成两条约束轮廓线，再运用以前的平行轮廓线建模方法进行。

2 在工程实例中的应用

2.1 研究区域数据特征

矿体模型表面是由矿山勘探、开采过程中获得的一系列矿山地质数据联合约束构成的空间三维实体，传统的矿山数据模型的构建是基于勘探线中较为整齐的钻孔数据，钻孔的布设通常是沿勘探线方向以40～70 m的间距钻探，这样对分布较为整齐的钻孔上见矿点数据进行提取处理，便可绘制较为可靠的矿体分布图。如图6(a)所示，横向排列实线代表勘探线，纵向排列实线代表钻孔，纵向实线上的点代表钻孔上的见矿点位置，每条勘探线应等距分布多个勘探钻孔。

内蒙古油篓沟矿区开采过程没有严格按照要求执行，每条勘探线所分布的钻孔只有一个，钻孔数据缺失，很难通过钻孔数据来勾勒矿体形体。如图6(b)所示，横向排列实线代表了实际勘探线布线走向和数量，纵向实线代表了实际钻孔数量，可知无法确定矿体具体轮廓。在此情况下，利用通过穿脉数据的分布大体估算矿体形态。如图6(c)所示，点状虚线为实际开采过程中的穿脉数据线，长虚线为推断的矿体表面界线。通过同一中段的一系列穿脉数据所构成矿体横截面平面与矿体轮廓线构成的纵剖面形成交叉剖面，多个中段层次的穿脉构成的横截面与纵剖面便可形成真三维立体的矿体模型。

2.2 见矿点数据提取

见矿点是钻孔或穿脉掘进过程中遇到的含有符合含矿量要求的矿段，其在空间中的分布特征在一定程度上可以反映出该区域矿体的形态特征，因此，利用见矿点的位置可以勾勒矿体轮廓，该位置矿体含矿量信息亦可以作为下一部矿体块段模型插值的数据基础。然而在工程图中，含矿矿段仅以相对位置标注并未提供真实的三维空间坐标，因此需要通过对工程文件解读，对见矿点的坐标位置以及含矿量进行解析。

如图7所示，穿脉数据图记录了穿脉开采的起始端和终止端坐标，图中灰色条形代表整条穿脉，黑色条形代表在穿脉开拓过程中的出现的含矿区域即见矿点，通过穿脉数据下的标尺记录见矿点相对于开采起始端位置的相对距离。因见矿点的解析过程是对钻孔或穿脉中各点的位置进行投影，获得该点位于该穿脉或钻孔起始点的相对位置，依据首末端空间位置坐标以及该坐标计算得到的穿脉的方向倾角，依据二三维转换坐标公式将相对位置转为含有空间坐标的绝对坐标位置。

2.3 矿体三维模型实现

据上述穿脉数据提取算法实现对穿脉数据的提取，并以不同将穿脉中见矿点数据所含矿品位值以不同颜色区分显示如图8(a)所示。根据1.2所述建模思路，利用穿脉数据中提取到的见矿点数据，以两端数据作为矿体两面的约束条件进行矿体三维建模，得到如图8(b)所示的三维可视化矿体图。

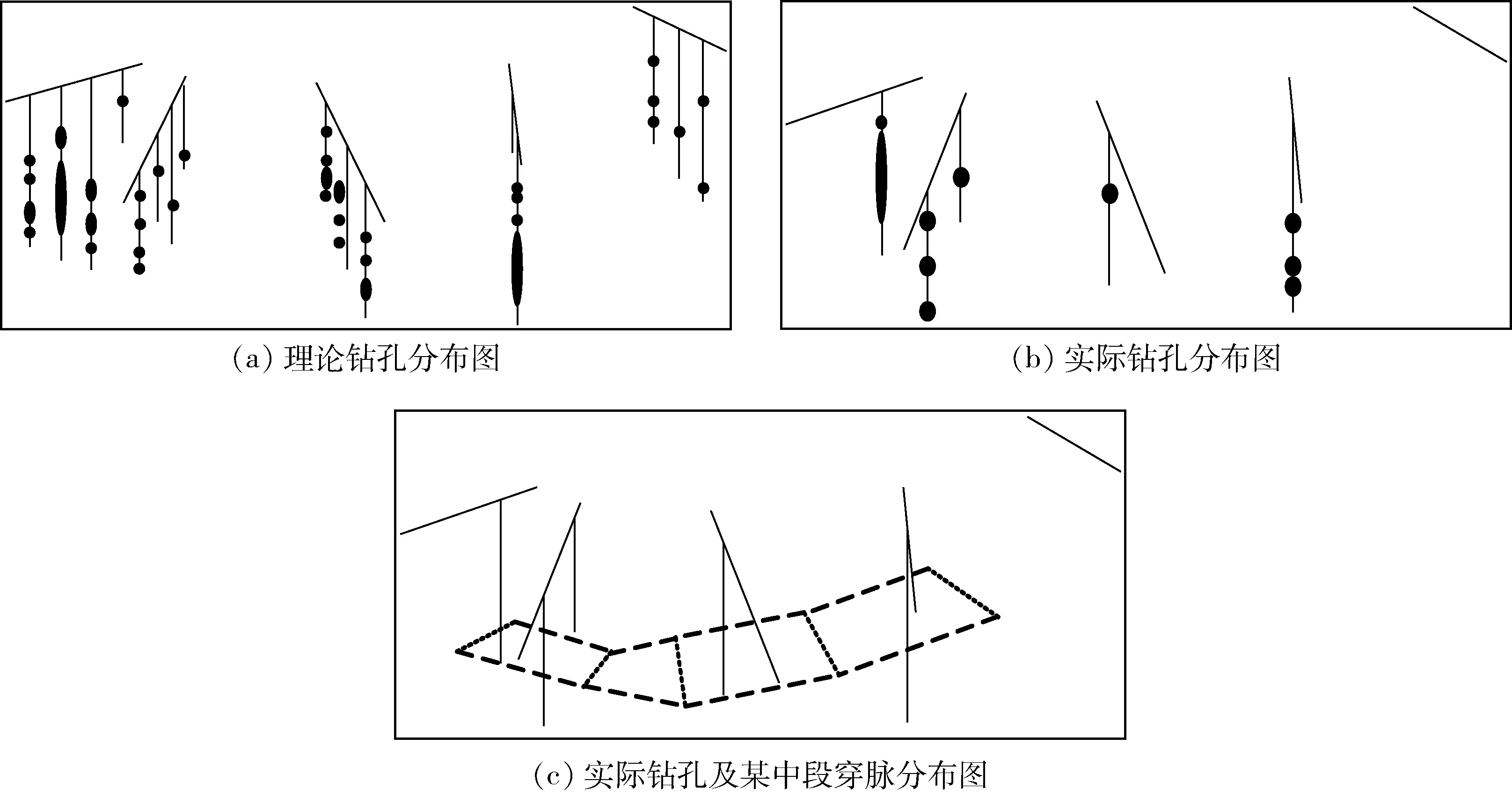
图6 钻孔分布对比图Fig.6 Drill distribution comparison

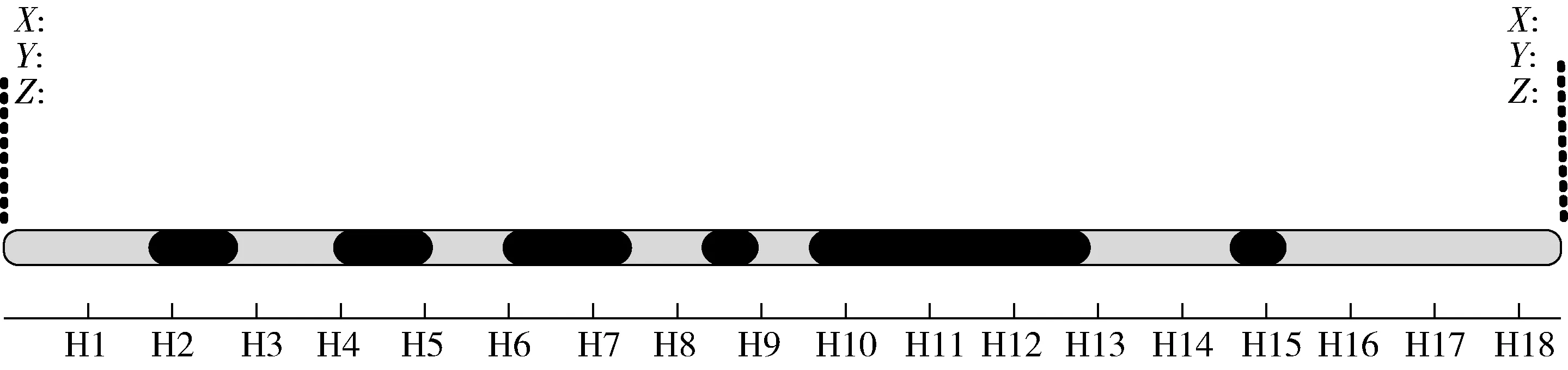
图7 见矿点示意图Fig.7 Mineral occurrence of tunnel

图8 矿体模型图Fig.8 Model of ore body

3 储量估算结果分析

对矿体的储量估算是对矿区地下矿产资源的埋藏量进行预估，目的是为矿山开采提供准确的数据依据，掌握矿石赋存状态，进一步指导矿山开采设计。利用矿体轮廓线进行储量估算一般采用断面法，通过轮廓线平面将矿体分为几个矿体区域，分别计算该区域矿体平均品位、矿体真厚度、体积等，通过计算得到该矿体资源量。通过该方法对传统平行轮廓线建模进行储量估算与穿脉约束下三维建模储量估算进行计算。按照生产详查报告进行的储量估算是含金量2 369.13 kg，三维建模储量估算结果为2 372.81 kg，可见穿脉约束下矿体三维模型对储量的估算结果更为接近。

4 结 语

在由矿体轮廓线进行矿体三维模型建模过程中采用穿脉数据对矿体表面形态进行约束，给出的穿脉数据提取算法可以获得穿脉中见矿点的真实地理坐标，丰富了矿体三维建模的可利用数据源；提出的穿脉数据与轮廓线数据连接方法，较好地解决了两类数据的匹配问题；给出的穿脉数据约束下的矿体建模算法有效的还原了矿体表面复杂的形态特点。基于WebGL的Three.js实现模型构建，最终建立web端的金属矿三维建模软件，并采用内蒙古油篓沟矿区地质勘探和采掘数据作为源数据进行实验。实验结果表明，通过穿脉数据约束下金属矿体三维建模可以提高矿体表面形态模拟的精度，以便于提升储量计算精度来指导矿山生产，亦可以作为在可用钻孔数据较少的情况下进行矿体真三维建模的方法。