初中几何课堂教学中学生发散思维的培养

江苏省南京市沿江中学 李玉文

发散思维在大多数心理学家的理论中是创造性思维最主要的特点，具体表现为人类在思考时拥有扩散性的思维方式，能够将个人的思维或者观念向多个方向拓展，对同一个问题作出多种回答，往往能够产生具有创新性的观点。数学具有非常强的逻辑性，需要学生大量地应用思维，《初中数学课程标准》中也指出在数学的学习中应当通过传授知识的方法发展学生的思维。由此可见，数学的学习和发散思维的培养是密不可分的，这就对我们的数学教学提出了更高的要求，笔者在此简谈一些自己在初中几何教学中培养学生发散思维的方法。

一、课堂教学中的发散思维培养

勾股定理是初中数学中较为重要的一个内容，虽然定理的内容非常简单，但是作为一个拥有多种精彩的证明方法并且在初中知识范围内的定理，可以作为启发学生应用发散思维的优秀素材。笔者在讲解三角函数时，除了在章节内向学生讲解多种证明方法，随着学生数学知识的增加，笔者也向学生讲解了与所学知识相关的勾股定理的其他证明方法。

例如在学习到相似三角形时，可以向学生讲解利用相似来证明勾股定理的多种方法，笔者在此例举其中一种证明方法：

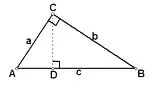
图1

证明：在图1 中，过C点作Rt △ABC的垂线交AB于D，

易得，△ACD～△ABC。

同理可得：BC2=BD·AB，

∴AC2+BC2=AD·AB+BD·AB=（AD+BD）·AB=AB2。

另外，在教学圆的部分的时候，也可以用三角形的内切圆或者切割线定理来证明勾股定理，在初三复习时也可以用反证法向学生证明勾股定理。

二、习题讲解中的发散思维培养

对于学生来说，学习中学数学的目的就是要让自己善于解题，而教师更应该教会学生灵活利用知识解决题目。在中学数学中，一道题目往往有多种解法，而教师在讲解习题时向学生介绍多种解法可以教会学生从多个角度分析问题，拓宽解题思路，在几种方法的比较中选择最适宜的方法，提高学生的解题效率，可以有效地训练其发散思维。

例如：如图2，点D、E分别是等边三角形ABC的边BC、AB上的点，∠ADE=60°，点M在AC上，满足∠ADM=60°，求证BE=MC。

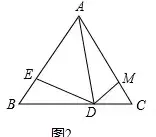
图2

解法1：

易得：△BED～△CAD，△ABD～△DCM，

解法2：

易得：△ADE～△ABD，△ACD～△ADM，

∴AD2=AE·AB=AM·AC。

∵AB=AC，∴AE=AM，∴BE=MC。

解法3：

如图3，在线段ED上截取M’D≡MD，连接AM’，

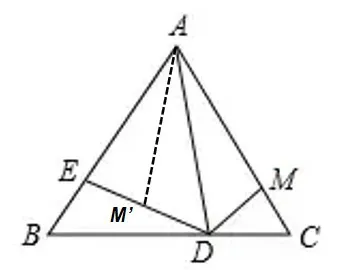
图3

易得：△M’AD≌△MAD，∴AM’=AM。

∵∠BAC+∠EDM=180°，

∴∠AMD+∠AED=180°，

∠AM’D+∠AM’E=180°，

∴∠AEM’=∠AM’E，

∴AE=AM’=AM，∴BE=CM

除了上述几种方法，这道题还可以利用翻折、旋转和四点共圆等方法解决。

三、探索型任务中的发散思维培养

在现在校内的数学教学中，虽然老师和学生的互动性增强了，但是大多数老师往往忽视了对学生学习主动性的培养，教师在课堂上与学生的互动中往往倾向于一小部分学生，对剩下的学生的“忽视”往往使其丧失主动性。在课堂上，我们不妨将学生分组，使其在一个团体中进行讨论，一方面能够调集更多学生的主动性，另一方面，多人进行讨论能够使学生听到别人的想法，扩散自己的思维。而作为教师，我们该做的则是引导学生进入任务情境，而情境创设则需要贴近生活或者具有实践性，再对学生进行合理的分组，以达到调动每个学生积极性的目的，在学生讨论探索结束后，在每个小组中选出代表来发言，最后再对学生的想法进行点拨、总结以及深化。

不仅在课堂上，我们在课下也可以给学生布置总结思考类的任务，在某些程度上减少重复的书面作业。例如，在讲解几何中的最短路径问题时，笔者并非布置大量的练习来对学生进行训练，而是让学生回去总结、查阅或者思考最短路径问题的解题方法，现在互联网中的资源十分丰富，为学生自主思考以及拓宽知识面奠定了良好的工具基础。

数学的学习和发散思维的培养是相辅相成的，为了培养学生的发散思维，教师应该营造良好的思维环境，给学生奠定扎实的思维基础，另外需要注意的是在注重培养发散思维的同时，不能违背数学的逻辑性、严谨性。教师应当在教学中注重思考，抓准进行发散思维培养的时机，需要进行反复的推敲，以获得更加科学有效的教学方式。