引信多普勒频率的线性稳健拟合
2019-12-20裴喆
裴 喆
(92941部队,辽宁葫芦岛125000)
防空导弹前向探测无线电引信在弹目接近时实时测量多普勒频率。多普勒频率不仅是导弹飞行试验分析引信启动和引战配合结果的重要参数,还可作为光测辅助手段估算导弹脱靶量[1-4]。由于体目标效应影响多普勒频率经常包含误差(尤其野值)[2-7],给结果分析带来困难。文献[1]研究了基于非线性最小二乘的多普勒频率拟合以及利用拟合残差去除野值的方法;文献[2]研究了非线性最小二乘拟合和小波分解相结合的方法,可去除野值比例达1/3,但野值识别和替换步骤有些复杂。为此,本文提出一种多普勒频率的线性稳健拟合方法,该方法的抗野值能力更强,步骤却更简单。
1 引信多普勒频率线性转换
1.1 引信多普勒频率数学模型
防空导弹与目标遭遇时间短,可认为弹目相对速度Vr保持不变,弹目遭遇过程如图1所示。

图1 弹目遭遇过程Fig.1 Missile-target encounter process
图1 中:ρ 为脱靶量(ρ 垂直于Vr);tρ为脱靶时间。则多普勒频率理论值为[1-3]:

式(1)中:λ 为引信工作波长;Vr通常可由导引头测量得到。
由于引信近程探测的体目标效应影响,引信多普勒频率实测值fd(t)的中后段会出现起伏,这种起伏可用加法性误差ε(t)表示,即:

取Vr=1 000 m/s 、tρ=20.000 0 s 、ρ=10 m ,在Fd(t)中后段加入白噪声误差ε(t)~N(0,σ20)合成模拟的实测值fd(t)。σ0=800 Hz,Fd(t)和fd(t)如图2所示。

图2 多普勒频率理论值Fd(t)和实测值fd(t)曲线Fig.2 Theoretical Doppler Fd(t) and actual Doppler fd(t)
多普勒频率拟合的目的就是滤除fd(t)中的ε(t),使拟合曲线尽量逼近Fd(t)。因导弹引战配合延时需要,引信须在tρ到来前引爆战斗部。所以,ρ 和tρ为未知量,但tρ和ρ 可由fd(t)拟合估计得到。一次弹目遭遇时ρ 和tρ是唯一的,因而ρ 和tρ的估计精度可用来衡量fd(t)的拟合精度。
1.2 引信多普勒频率线性转换

把式(3)等号左侧函数记为Fx(t),即:

再令K1=-1/ρ,K2=tρ/ρ,则得Fx(t)关于时间t 的一次线性函数为:

式(5)中:K1和K2为多项式系数,因而式(4)即为多普勒频率线性转换表达式。
同理,将fd(t)线性转换为fx(t),则fx(t)只与已知量fd(t)、λ 和Vr有关,而系数K1、K2只与未知量ρ、tρ有关。将图2 中的Fd(t) 和fd(t) 分别转换为Fx(t) 和fx(t),结果如图3所示。

图3 多普勒频率线性转换的Fx(t)和fx(t)曲线Fig.3 Fx(t) and fx(t) of Doppler linear transform
对fx(t)线性稳健拟合估计得到K1和K2,计算出ρ 和tρ,再利用式(1)即可计算fd(t)的拟合结果。
2 线性稳健拟合方法
2.1 线性稳健拟合及其权重函数
普通最小二乘拟合给予每个测量数据的权重均为1,而拟合目标是使残差平方和最小,因而拟合结果受野值(也称异常值、粗差)的影响较大。稳健拟合就是为抵抗野值发展起来的。目前,线性稳健拟合理论较为成熟,主要有包括L估计、R估计和M估计等多种方法[8-9]。本文采用M估计法,它将经典极大似然估计的思想推广用于稳健拟合[8,10],其基本思想是采用迭代加权最小二乘法估计多项式系数,根据权重函数确定残差的权重大小,残差越大,权重越小,从而达到抵抗野值的目的[11-12]。
选择合适的权重函数是M估计法的重要环节,比较典型的函数有Huber、Bisquare、Andrew 等。根据fx(t)的误差特性,本文采用Bisquare权重函数(也称双平方权重函数),即[8,13]:

式(6)中:y 为归一化残差;cB为调节常数(通常取4.685)[8],对绝对值大于cB的残差,其权重均为0。
求解基于M 估计的线性稳健拟合需要使用迭代加权最小二乘法[14],比较简便的方法是直接采用Matlab、R 等常用数学软件的内置函数,本文采用Matlab软件的robustfit函数[15]。
2.2 多普勒频率线性稳健拟合方法及步骤
由式(4)将多普勒频率实测值fd(t)线性变换成fx(t),对fx(t)进行线性稳健拟合的方法及步骤如下:
1)对fx(t)进行第1 次稳健拟合,得到系数K1、K2的第1 次估计值以及拟合直线fxn1(t);由K1、K2计算ρ、tρ的第1 次估计值,再利用式(1)计算fd(t)拟合值fdn1(t)。
2)计算拟合残差εxn(t)=fx(t)-fdn1(t),再计算εxn(t)的中位数绝对离差MAD,公式为[16-17]:

式(7)中,MED 为中位数。
MED 是稳健拟合中重要的位置测度,MAD 是重要的尺度测度,他们的抗野值能力都很强。为此,基于MAD 计算稳健拟合标准差σxn=MAD/0.674 5[16];最后,将拟合残差绝对值>3σxn的数据fx(tk)判别为野值,并将其修正为对应的拟合值fxn1(tk),得到新的fx(t)。
3)对新的fx(t)进行第2 次稳健拟合,得到系数K1、K2的第2 次估计值以及拟合直线fxn2(t),再计算ρ、tρ的最终估计值以及fd(t)的最终拟合值fdn2(t)。
3 拟合方法仿真验证
3.1 仅含随机误差时的稳健拟合结果
图2 中,fd(t)数据仅含随机误差,曲线起伏较小。图3 中,fx(t)为其线性转换数据。仅执行步骤1),对fx(t)进行稳健拟合得到拟合直线fxn1(t)如图4 所示。可见,fxn1(t)几乎与理论值Fx(t)重合。同时,得到ρ 和tρ的估计值分别为10.025 m 和20.000 2 s,生成的拟合值fdn1(t)也非常逼近理论值Fd(t)(图略)。

图4 fd(t)仅含随机误差时的稳健拟合结果Fig.4 Robust fitting result when fd(t) contains random errors
为进行比较,用蒙特卡洛法对fd(t)进行非线性最小二乘拟合[1-2,18]、fx(t)进行普通线性最小二乘拟合、以及fx(t)进行稳健拟合(2 种权重函数)分别仿真1 000次。每次加入不同的白噪声误差ε(t)~N(0,),σ0仍取800 Hz。 ρ 和tρ估计值的均值分别为10.000 m 和20.000 0 s,ρ 和tρ估计值的标准差(分别用σρ和σtρ表示)统计结果如表1所示。

表1 不同拟合方法ρ 和tρ 估计值的标准差统计结果Tab.1 Statistics results of standard errors of ρ and tρ in different fitting methods
分析表1 可知:仅含随机误差时,4 种拟合精度均很高,σρ均小于0.15 m 0,σtρ均小于0.3 ms;但稳健拟合精度相对更高,尤其采用Bisquare 权重函数的本文方法。这是因为由式(6)可知,Bisquare函数对绝对值不大于cB的中间段残差也进行权重分配,越靠近分布中心的残差其权重越接近1。
3.2 包含多个野值时的稳健拟合结果
主要讨论成片型(或斑点型)野值[2,10],且野值主要分布于曲线一侧的情形,因为这种情形对普通最小二乘拟合最为不利。在图2 所示fd(t)数据加入11 段成片野值(每段4~7个),野值数量比例为40%,加野值的fd(t)及其非线性拟合结果fdn(t)如图5所示,可见拟合值fdn(t)与理论值Fd(t)偏离较大,此时ρ 和tρ估计值分别为11.650 m 和20.001 4 s。如果利用拟合残差εdn(t)=fd(t)-fdn(t)识别野值,则会导致部分正常数据被误判为野值。可见,普通最小二乘拟合受野值影响较大,或者说拟合稳健性不强。
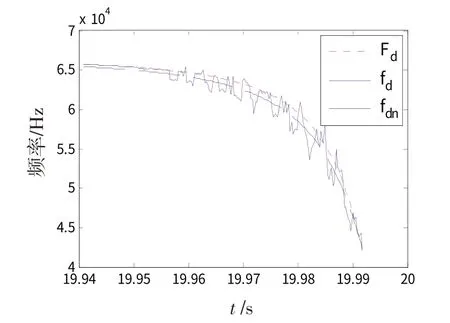
图5 fd(t)含野值时的非线性拟合结果Fig.5 Nonlinear fitting result when fd(t) contains outliers
将加野值的fd(t)线性变换成fx(t),对fx(t)先执行步骤1)进行第一次稳健拟合得到拟合直线fxn1(t),如图6 所示,fxn1(t)没有很逼近Fx(t),但偏离并不大,说明第一次拟合的稳健性就很好。此时,ρ 和tρ的第一次估计值分别为9.790 m 和19.999 0 s,相比fd(t)非线性拟合的估计精度明显提高。

图6 fd(t)含野值时的第一次稳健拟合结果Fig.6 First robust fitting result when fd(t) contains outliers
继续执行步骤2)和3),野值修正后的新fx(t)及其第二次稳健拟合直线fxn2(t),如图7所示。可见,fxn2(t)非常逼近Fx(t)。 ρ 和tρ的最终估计值分别为9.945 m和19.999 5 s,比第一次稳健拟合的估计精度进一步提高;同时,fd(t)最终拟合值fdn2(t)也非常逼近Fd(t),满足引信启动和引战配合分析需要。

图7 野值修正后的稳健拟合结果Fig.7 Robust fitting result after correcting outliers
4 结论
本文研究了引信多普勒频率的线性稳健拟合方法,将常用的多普勒频率非线性拟合转换为线性稳健拟合。研究表明:该方法充分利用了线性稳健拟合抗野值能力强的特点,多普勒频率野值比例为40%时的拟合精度仍很高;同时,该方法仅需2次线性稳健拟合和1次野值修正,步骤简单、编程实现容易。方法可用于飞行试验引信启动和引战配合结果分析,也可用于导弹脱靶量估算。
