管道轴向导波检测技术
2019-12-19郑玲慧任尚坤
郑玲慧,任尚坤
(南昌航空大学 无损检测技术教育部重点实验室,南昌 330063)
0 前 言
钢管是一种被广泛应用的重要钢材品种,钢管应用相关行业的经济效益及人员的生命安全与钢管的质量息息相关[1]。 作为输送加压液体或气体以及固体和液体混合物的工具,管道广泛用于石油设备制造、电力建筑工程、化工等领域。 但在常规应用中,由于恶劣的工作条件等因素,腐蚀、疲劳等失效形式极易出现在在役管道中,导致管道的使用寿命较预期缩短,甚至出现管道泄漏等事故,造成巨大的资源浪费和经济损失。 为了防止由腐蚀穿孔、泄漏、管道爆炸等引起的恶性事故的发生,对管道进行快速有效的无损检测非常重要[2]。
导波是一种可以沿波导 (管状结构或板状结构) 的纵向进行长距离传播的超声波[3],因此,超声导波检测技术在检测的快速、远程和低破坏性方面被认为具有巨大的潜力。 导波检测是无损检测行业的一种新型检测技术,具有检测距离长、缺陷检出能力强、对人身无危害等优点,其重要性正随着应用范围的不断扩大越来越得到凸显[4]。 另外,导波检测环境除地上和地下外,在海洋管道的检测中的应用也已有实质性的进展[5-6]。与常规超声波中的横波和纵波不同的是,当超声波在介质的不连续边界处发生不断往复反射和叠加时,即形成超声导波[7]。 当选用柱状或管状的波导产生超声导波时,一共出现3 种模态的超声导波,即扭转模态导波、纵向模态导波和弯曲模态导波[8-9]。 NISHINO H[10]等研究了导波在空心圆柱中的频散特性,发现管子的厚径比 (t/D) 对导波频散影响很大,当t/D 很小时,管子中产生的纵向模态导波和扭转模态导波可分别对应于板子中的Lamb 波和SH 波。 OGI H[11]等在研究管道壁厚减薄检测中,使用电磁超声传感器 (electromagnetic acoustic transducer,EMAT) 在 铝管中激励出扭转模态导波,并通过测量模态转换引起的扭转导波群速度的变化来测量管道壁厚的减薄。 黄松龄[12]等通过比较板状和管状结构的波导,总结了不同模态导波传感器的特点,分析了导波与管道缺陷的相互作用,验证了导波在管道缺陷定位、尺寸量化和成像中的应用。 何存富等[13-14]模拟出扭转模态导波,并通过建立带有纵向缺陷的管道有限元模型,检测并定位出缺陷。
本研究对轴向导波检测技术在管道中的应用进行了系统综述,讨论了轴向导波产生的理论基础及其频散特性,着重论述了近年来轴向导波的传感技术,并对管道轴向导波无损检测技术进行了总结与展望。
1 轴向导波的理论基础
在无应力边界条件下,沿管道轴向传播的柱面导波由于振动现象可以分为如图1 所示的3 种模态。 这 3 种模态导波分别可以写成 L (0,m)、T (0,m) 和 F (n,m),其中 n (n=0,1,2,3,4…,n=0 对应的是轴对称模态,n=1,2,3…对应的是非轴对称导波) 是周向模态参数; m 是径向模态参数,表示该导波模态在管道轴向上的振动形态(m=1,2,3…)[15]。 MEITZLER[16]和 ZEMANEK[17]将圆周上所有的高阶模态都归类为F 模态,即T型模态只有周向基础模态 (n=0),扭转模态和纵向模态一样,被指定为轴对称模态,而F 型模态被指定为非轴对称模态。 图1 描述的是导波质点振动及波形传播的方向。 当质点振动的方向、波形传播的方向同时平行作用于管道表面时,激发出来的是L 型模态导波; T 型模态导波在平行振动方向上作用于管道表面,在垂直振动方向上作用于传播方向; F 模态在倾斜振动方向作用于传播方向,3 个方向上产生的振动均与管道表面相平行。 由于导波的自由震荡特性,可以认为这3 种模态的导波对缺陷的检出能力互不相同,对于长距离管道中的缺陷检测,既可以采用轴对称导波,也可选取非轴对称导波,但因为激发轴对称模态导波的方式更简单、接受信号易于处理,因此在实际检测中被广泛应用。
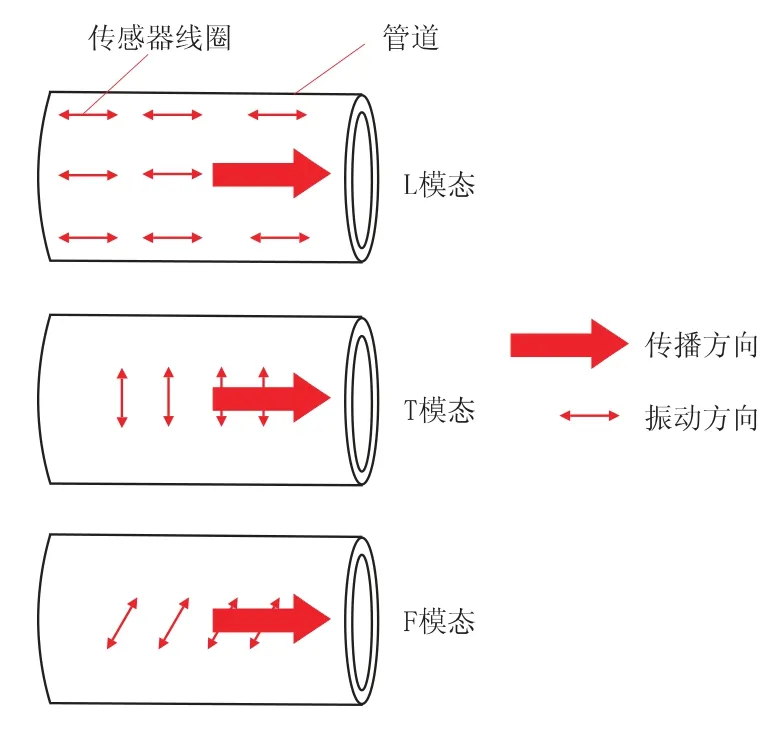
图1 管道中沿轴向传播的导波
在对导波的研究中,导波在板平面内产生和传播的机理,已具有比较系统的成果。 SILK M G[18]等证明了管道中的超声导波模态与Lamb 波是相对应的。 当管道为薄壁管 (直径远大于厚度) 时,其可以近似为展开的板平面,此时管道中的纵向模态导波和扭转模态导波分别对应板平面中的SH 波和Lamb 波。
群速度和相速度两个概念在导波理论研究中至关重要。 群速度是指在具有特定特征 (例如最大振幅) 的包络线上的声波速度,群速度(几乎)等于声能传播的速度; 相速度是简谐声波相位的传播速度,也是波群中单个子波的传播速度[19]。
频率为ω、波数为k 的简谐波可以写成

相位 φ 为

其中,cφ被定义为相速度

群速度与相速度不同,它与一组频率相近的声波群有关。 频率分别为 ω1、ω2,波数分别为k1、k2的简谐波可以写成

则相速度分别为

叠加后的声波可以写成
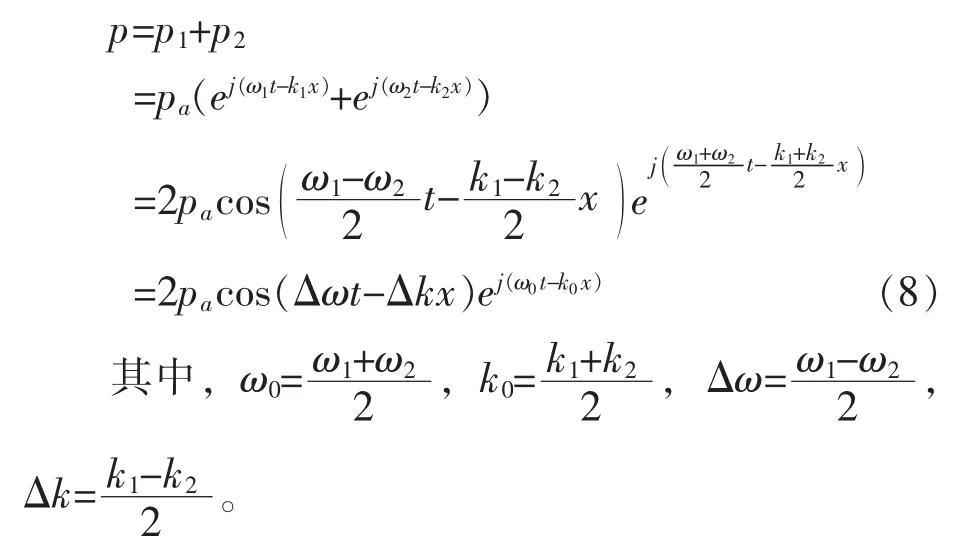
群速度为

取极限,则群速度也可表示为
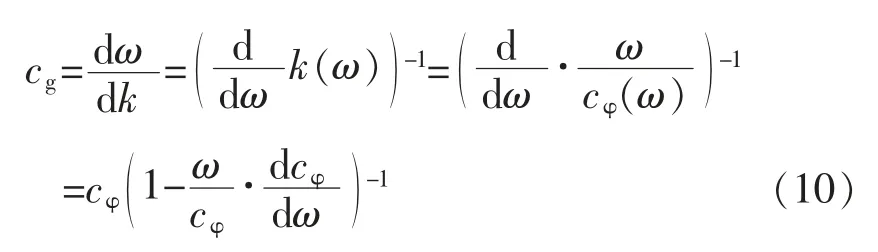
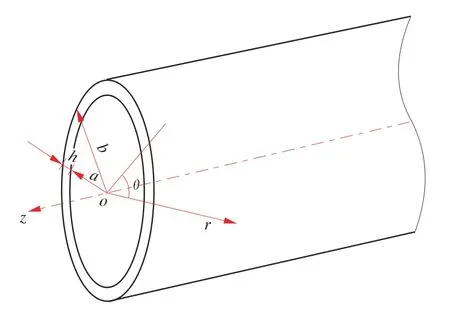
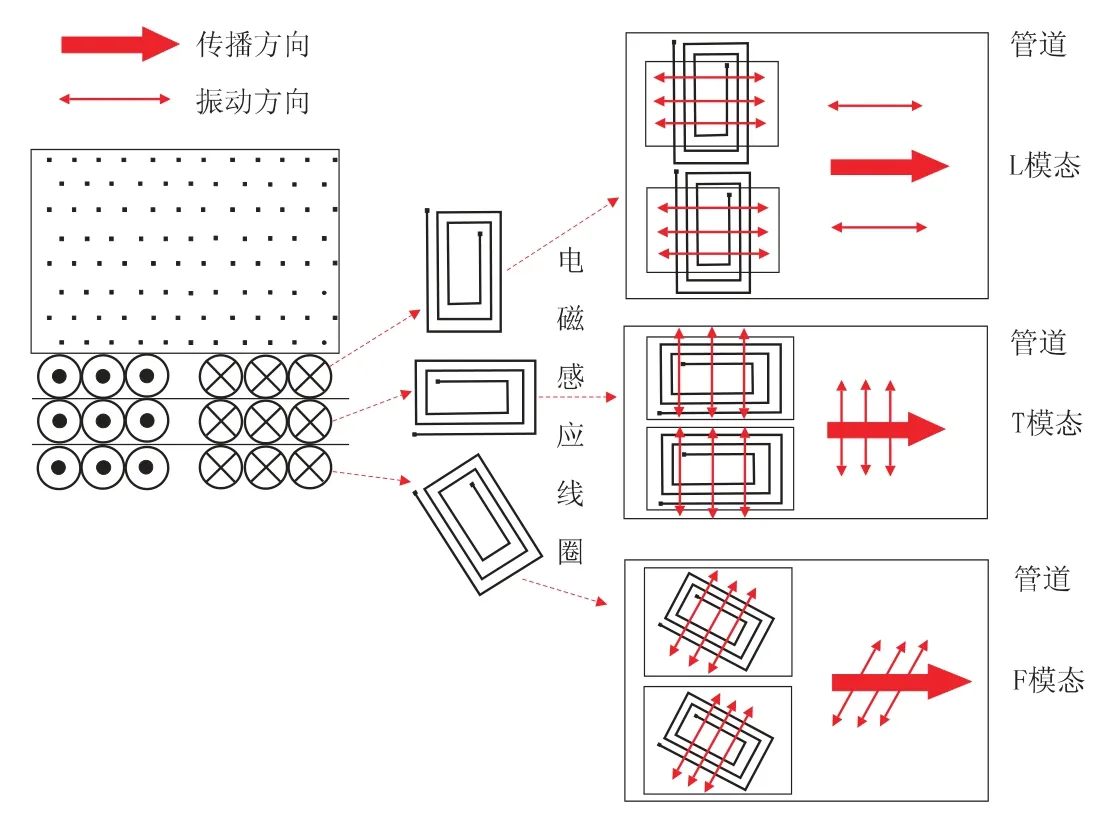
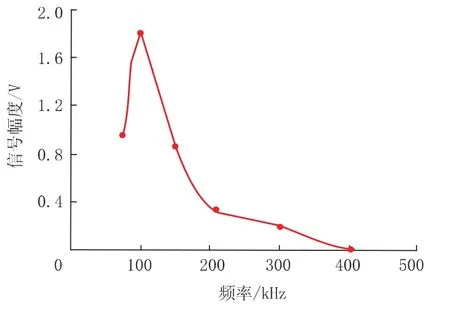
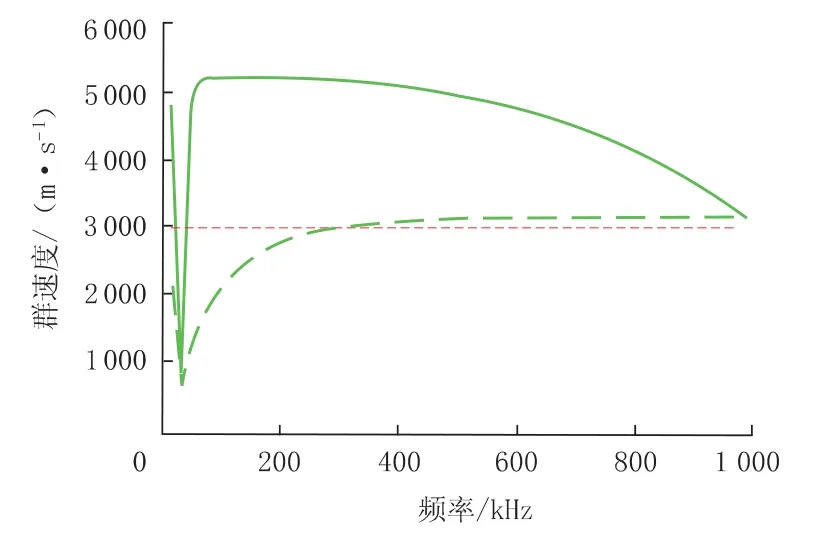
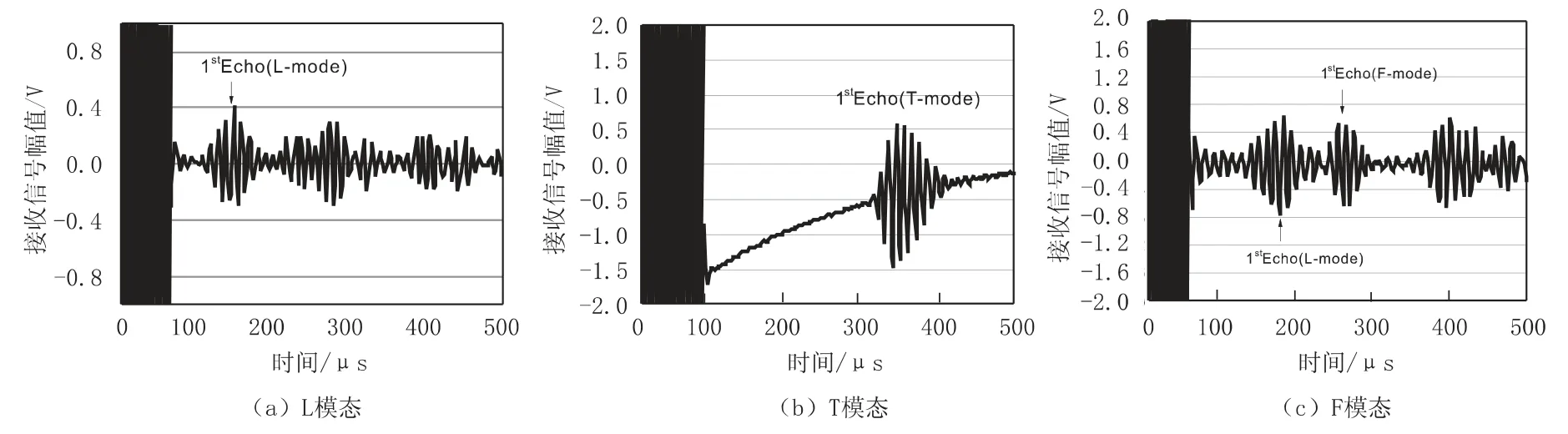
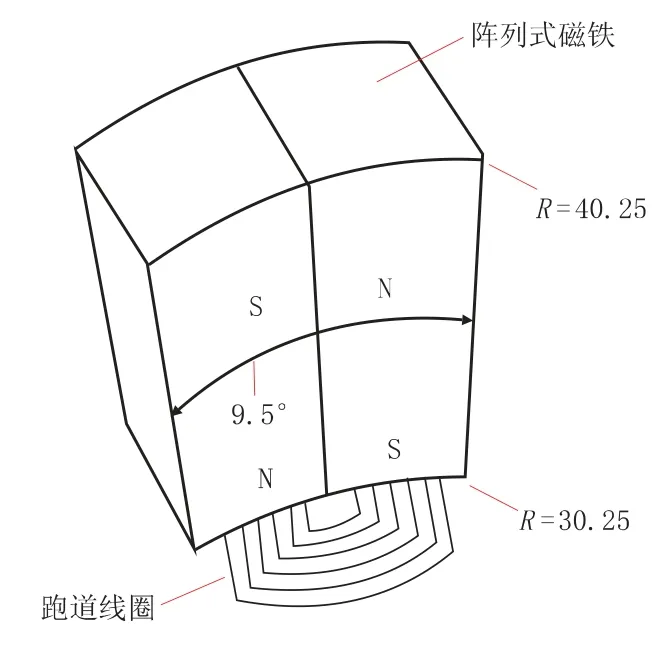
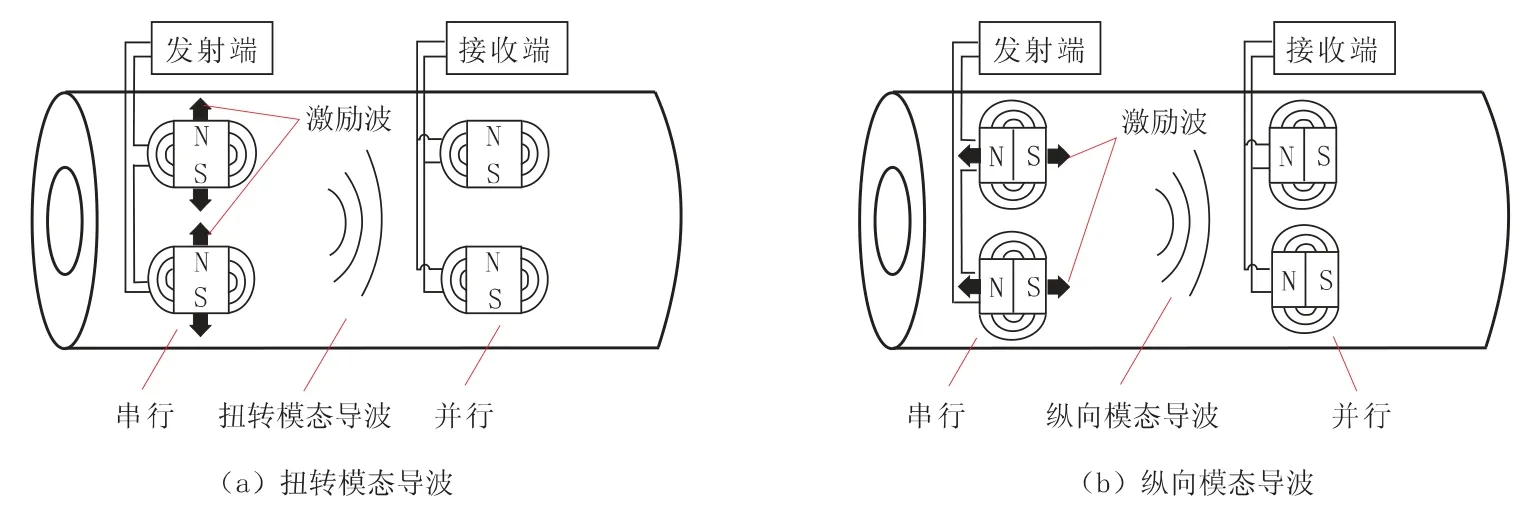
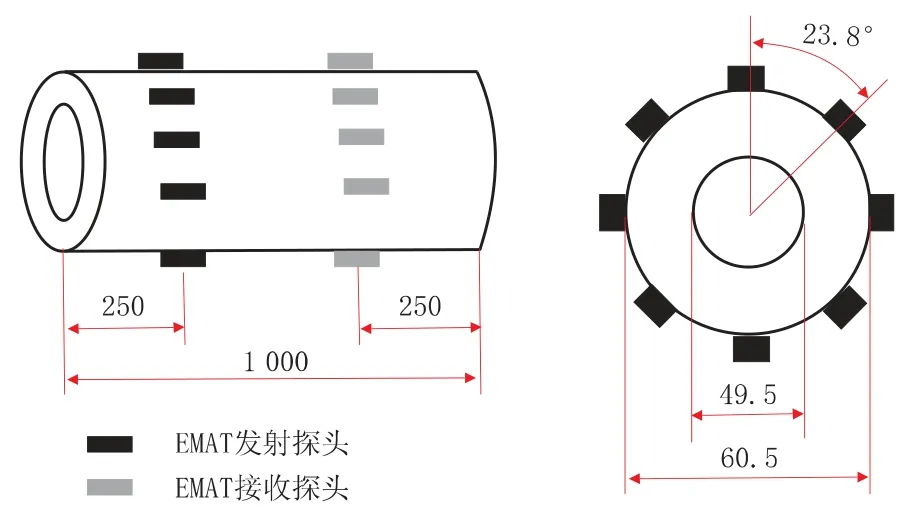
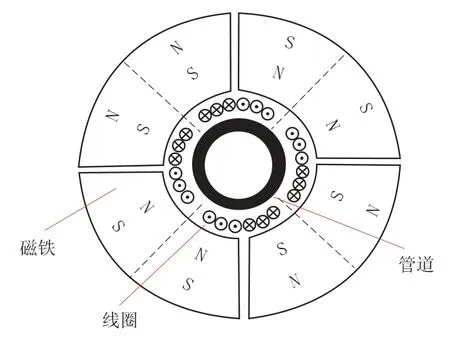
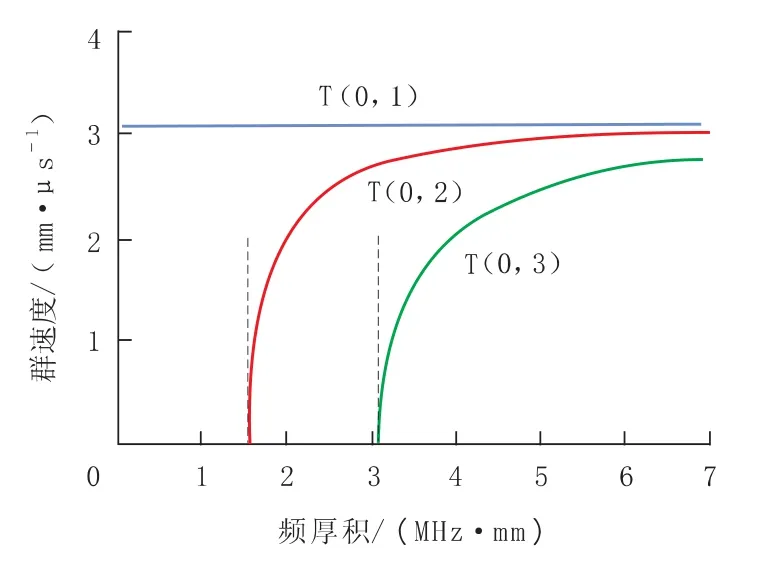
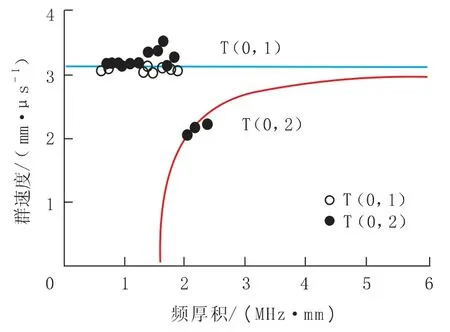
由公式 (10) 可以看出,群速度 cg和相速度 cφ通过联系在一起。 当时,cg=cφ;时,cg 频散是导波中的一个重要概念,由于声速是频率的函数,不同频率的声波以不同的相速传播,超声导波的频散使波包在结构中传播时在空间和时间上都发生了扩散,这就限制了长距离超声导波检测的效率[20]。 GAZIS D[15]在弹性线性理论的框架下,讨论了空心圆柱中导波的频散特性,最先给出了管子中导波的频散方程,并分别对产生3 种导波的频散条件进行了论述。图2 是一个无限长弹性管模型,其中z 是圆柱壳的中心线,a、b 分别为圆柱内半径和外半径,h 为壁厚。 图2 圆管模型示意图 在弹性线性理论的框架下,得到了以两个同心圆柱表面为边界的各向同性连续介质的特征模态的特征方程[15] 式中:u——位移矢量; ρ——材料的密度; λ 和μ——拉梅常数; ▽2——三维拉普拉斯算子; Ø——膨胀标量势函数; H——等容矢量势函数; F——坐标向量r 和时间t 的函数。 如果Ø 和H 满足波方程 则运动的位移方程为 式中:v1——管道的纵波波速; v2——管道的横波波速。 令 管子中导波的应力自由边界条件是在r=a,r=b 处有 结合公式 (19) 得到由振幅系数 A,B,A1,B1,A3,B3的行列式构成的特征方程,则超声导波在管子中传播的频散方程为 其中 i 表示行,j 表示行列式的列。 令 此即为弯曲模态的频散方程。 当周向阶次 n=0 时,公式 (19) 可分解为次行列式的积[15] 其中, 只有 D1=0 或 D2=0 时,才满足公式 (21)。 当D1=0 时,涉及到位移分量 ur和 uz,对应纵向模态导波; 当 D2=0 时,只涉及 uθ,即对应于扭转模态导波。 所以要得到管子中纵向导波和扭转模态导波的频散曲线,只需分别对C1=0 和C2=0 求解。由此可以看出,导波在管道中传播具有多模态频散特性,不同行列式的解对应于不同模态的导波。 传统的导波检测系统大多采用压电传感器(PZT) 设计。 传统的压电式超声导波传感器虽然有着检测效率高、稳定、工人对操作流程熟练等明显的优势,但其在检测过程中对被检工件表面状态要求高、需高粘度的耦合剂、不能在高温或低温下进行检测等缺点也使得电磁超声导波传感器吸引了众多学者的研究并取得了快速的发展。 电磁超声传感器 (EMAT) 是一种用于非接触式超声激励和接收的传感器,不需要任何耦合装置。 每个EMAT 都可以被设计成多通道操作,且具备压电传感器的功能。 与传统传感器相比,EMAT 具有许多优点,如操作简单、耐高温、经济等。 此外,EMAT 是可以成为产生 L 型、T 型和F 型导波的驱动器,这为工厂的现场检查和在线监控提供了优势。 电磁超声传感器结构如图3 所示。 电磁超声传感器由被检材料、在厚度方向上施加磁场的永磁体以及一个在被检材料表面上施加涡流的电磁感应线圈组成。 根据弗莱明左手定律,在表面水平方向和涡流垂直方向上产生洛伦兹力,根据电磁感应线圈高频电流中涡流的高频振动,洛伦兹力发生周期性的变化,然后转换成超声导波。 图3 电磁超声传感器结构 MURAYAMA R[21]等研制了一种新型的EMAT检测系统,该检测系统可以交替使用三种模式,如图4 所示[21]。 通过改变线圈的方向可以分别激发出L、T 和F 三种不同模态的超声导波。 这种涡流可以用矩形线圈或椭圆线圈产生,在金属材料上放置的EMAT 可以向任意方向旋转,从而产生任意振动方向的横波,并通过EMAT 系统能够检测到足够强的这三种模态导波信号。 该EMAT 导波检测系统对不同驱动条件进行了测试,获得了良好的接收信号,如图5 所示[21]。 由图5 可知,在 100 kHz 的驱动频率下,该EMAT 导波检测系统可获得相对更稳定的信号。 图4 使用EMAT 的三种模态导波系统 图5 信号幅度和驱动频率的关系 选用直径60 mm、厚度2 mm 的铝管,铝管导波的驱动频率与导波群速度的关系如图6 所示[21]。使用 100 kHz 驱动频率时,L(0,2)为 5 230 m/s;T(0,1)为 3 130 m/s; F(0,1)为 2 780 m/s。 调整后的接收信号如图7 所示[21],由图7 可以看出,T(0,1)模态接收的信号最好。 图6 铝管导波的驱动频率与导波群速度的关系 图7 三种模态调整后的接收信号 FURUSAWA A[22]等研究了一种利用电磁超声换能器 (EMAT) 环形阵列来激励和接收扭转和纵向模态导波的方法,证明了在圆周方向上按一定间隔排列的EMAT 能够激发和接收L 与T 模态导波。 EMAT 的设计方法如图8 所示[22],EMAT选用了阵列式永久磁铁和跑道线圈。 图9 为环形阵列式 EMAT 结构分布[22],采用的是电磁超声换能器环形阵列,发射端和接收端的EMAT 分别采用串行和并行数据传输方式以增强信号的强度。 图9 (a) 是使激励的导波作用于周向,是用于扭转模态导波激励的电磁超声传感器。 图9 (b) 仅将图9 (a) 中的 EMAT 装置旋转90°,使激励的导波沿轴向传播,即可产生纵向模态的导波。 利用EMAT 接收导波的原理与激励相同,接收导波时,EMAT 接收机的设置与EMAT 发射机相同。 图8 环形阵列式EMAT 探头结构 图10 为 EMAT 检测模拟示意图[22]。 选取一根钢管,设有两个EMAT 环形阵列用于发射和接收,每个EMAT 环形阵列在圆周方向上每隔一定的间隔有8 个EMAT,当前置放大器的激励频率设置为不同的频率时,可分别对应激发出一阶扭转模态导波T(0,1)、一阶纵向模态导波L(0,1)以及二阶纵向模态导波 L(0,2)。 图9 环形阵列式EMAT 结构分布示意图 图10 EMAT 检测模拟示意图 在用于管道检测的导波中,扭转导波具有一些特殊的优势,它仅由周向极化运动组成,受涂层和液体载荷的影响较小,因此可以缩短检测时间。 扭转导波无频散,在频率和厚度范围内都有相同的速度,即使对于更高模态,扭转波的频散曲线也相对简单。 但与其他导波相比,单一模态的扭转波的产生是相当困难的。 NURMALIA、NAKAMURA N[11,23]等研究了在管道壁厚减薄检测中,模态转换引起的扭转导波群速度变化问题。采用EMAT 进行扭转模态的生成和检测,每个EMAT 都有一个特殊的配置,即周期性永久磁铁(PPM-EMAT)。 它由一组永久磁体组成,以提供与试样表面垂直的周期性偏置磁场。 这些磁铁位于细长螺旋线圈顶部,螺旋线圈以曲流形式相互连接,以形成交流电源,沿轴向提供涡流。 导电材料附近两个磁场相互作用,在材料表面附近产生沿周向的洛伦兹力,从而产生偏振的剪切波。磁铁在轴向排列的周期性决定了所产生的波长。设计的EMAT 产生的扭转波的波长为5.22 mm。每个发射和接收EMAT 由围绕管道的四个PPMEMAT 组成。 图11[11]显示了它们排列的横截面视图,添加虚线是为了区分排列中的每个PPM-EMAT。 EMAT 共由 8 个周期的音频脉冲驱动发射。 根据驱动频率和波长的不同,相应的扭转模态会在试件中选择性地产生。 EMAT 接收部分有选择地接收传播模态,经放大后,接收到的信号被传输至信号处理单元。 图12[11]是在厚径比为3/25 的管道中传播的扭转模态群速度频散曲线,虚线表示对应模态导波的截止厚度。 除了T(0,1)模态外,每个高模态的群速度都高度依赖于波导的频率乘以厚度,尤其是在低频范围,当频率固定时,群速度随厚度的减小而减小。 图13[24]为实际频散曲线与理论频散曲线的对比。 由图13 可以看出,当厚度变化时,T(0,1)导波没有明显的变化,证实了T(0,1)模态的非频散性质,即群速度与厚度和频率无关。 图11 PPM-EMAT 排列横截面示意图 图12 扭转模态群速度频散曲线 图13 实际频散曲线与理论频散曲线的对比 管道轴向导波的理论基础是建立在板中导波理论基础之上,然而现实情况中,存在如弯管、特殊形状管道等情况,需要进一步研究特殊情况时管道中产生导波的处理方法。 在研究管道中导波频散现象时,发现共有3 种导波模态产生,但管道中激发的导波往往在模态上并不单一,如此对检测结果会产生较大的影响,故对于如何在管道中激发出单一模态导波的问题,还有待继续研究。 3 种模态中扭转模态具有无频散特性,但对扭转模态导波的研究很少,且大多集中在数值模拟、仿真分析方面,应进一步深入研究基于扭转模态的管道导波无损检测技术。2 轴向导波的频散特性
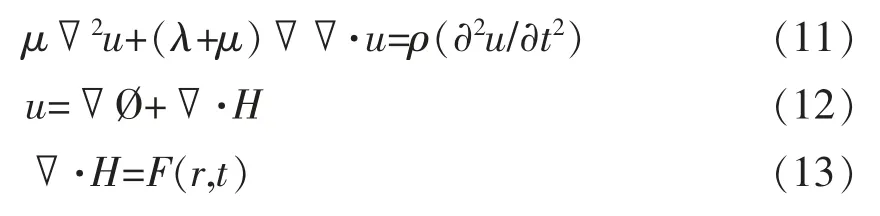




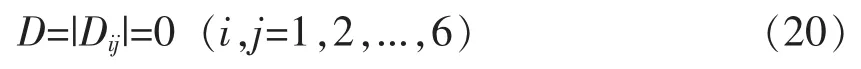
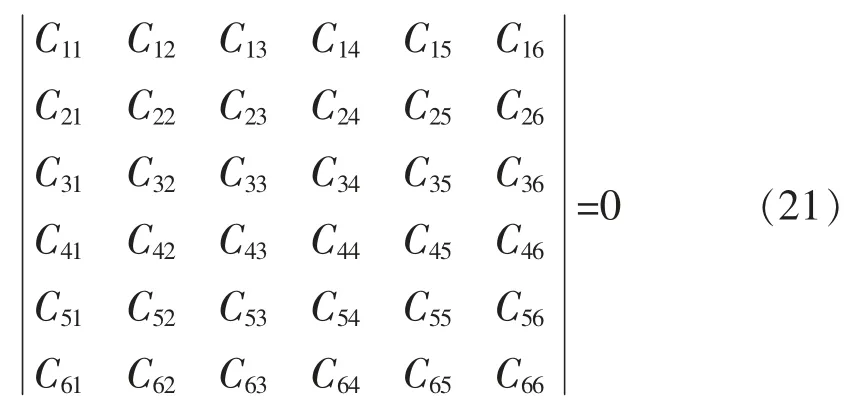


3 扭转导波的传感技术

4 结束语
