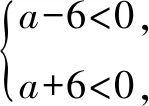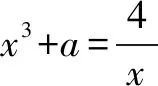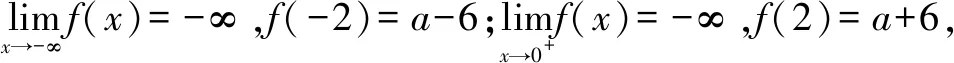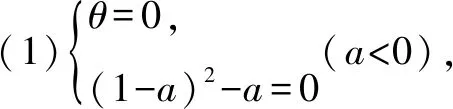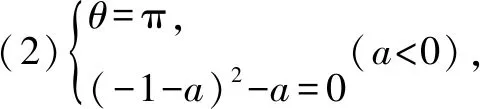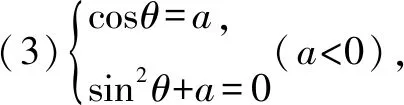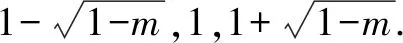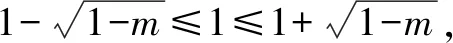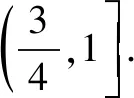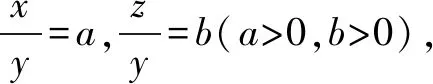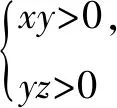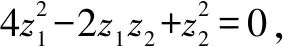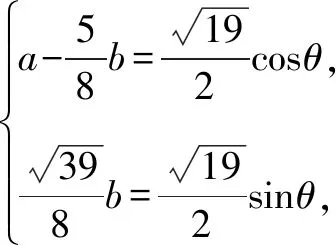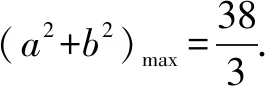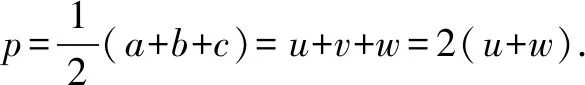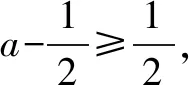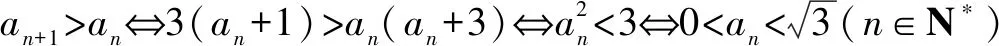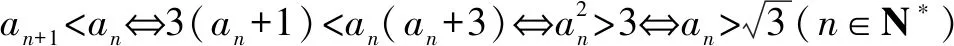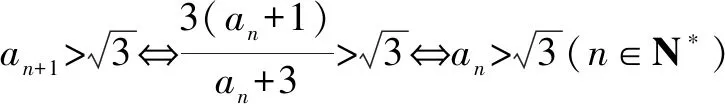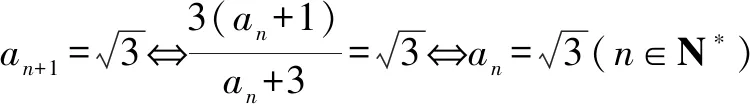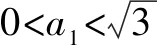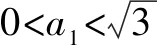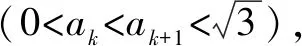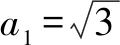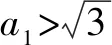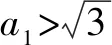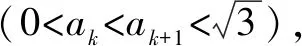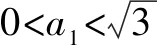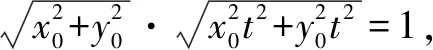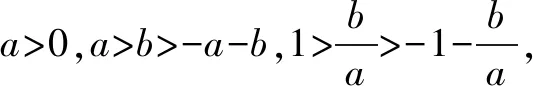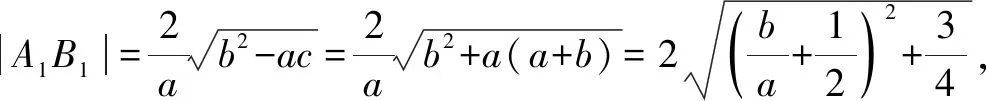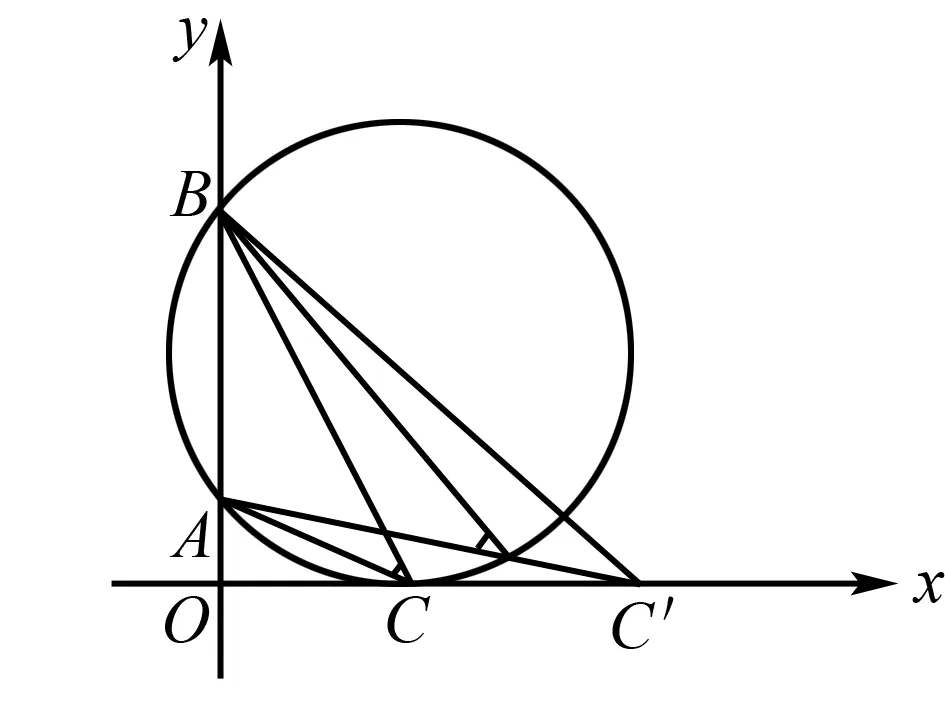2019年上海交通大学自主招生数学试题(部分)及其详解

2019-12-19甘志国

数理化解题研究 2019年34期

关键词：题设数学试题半轴

甘志国

(北京市丰台二中 100071)

2019年上海交通大学自主招生数学试题涉及集合、命题、函数、解三角形、平面向量、数列、不等式、立体几何、平面解析几何、二项式定理、复数与平面几何等内容，难度适中.文章还给出了部分试题的出处.

本文中的题目是笔者综合多位考生的回忆得到的，题目不全.解答由笔者独立完成.

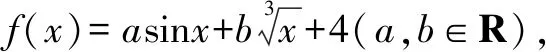
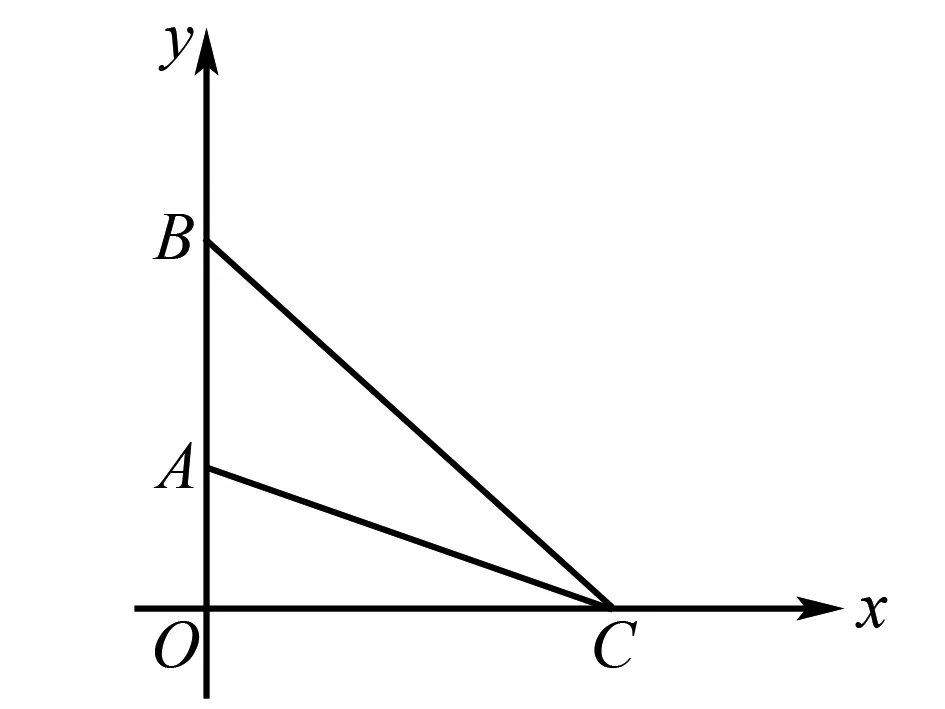
A. -5 B. -3 C. 3

D. 随a,b取不同值而取不同值

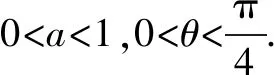
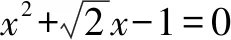
4.已知复数z满足|z|=1，且z2-2az+a2-a=0，求负数a的值.

5.若关于x的方程x3-3x2+(m+2)x-m=0的三个根是某个三角形的三边长，求实数m的取值范围.

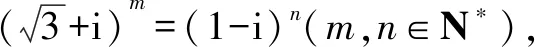
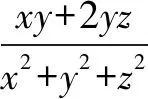
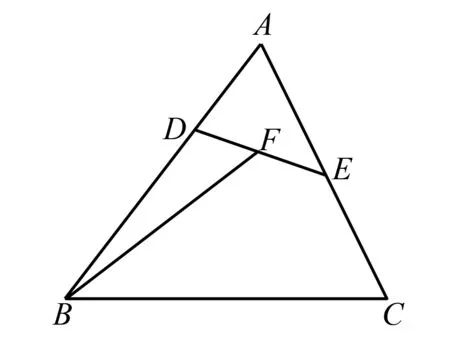
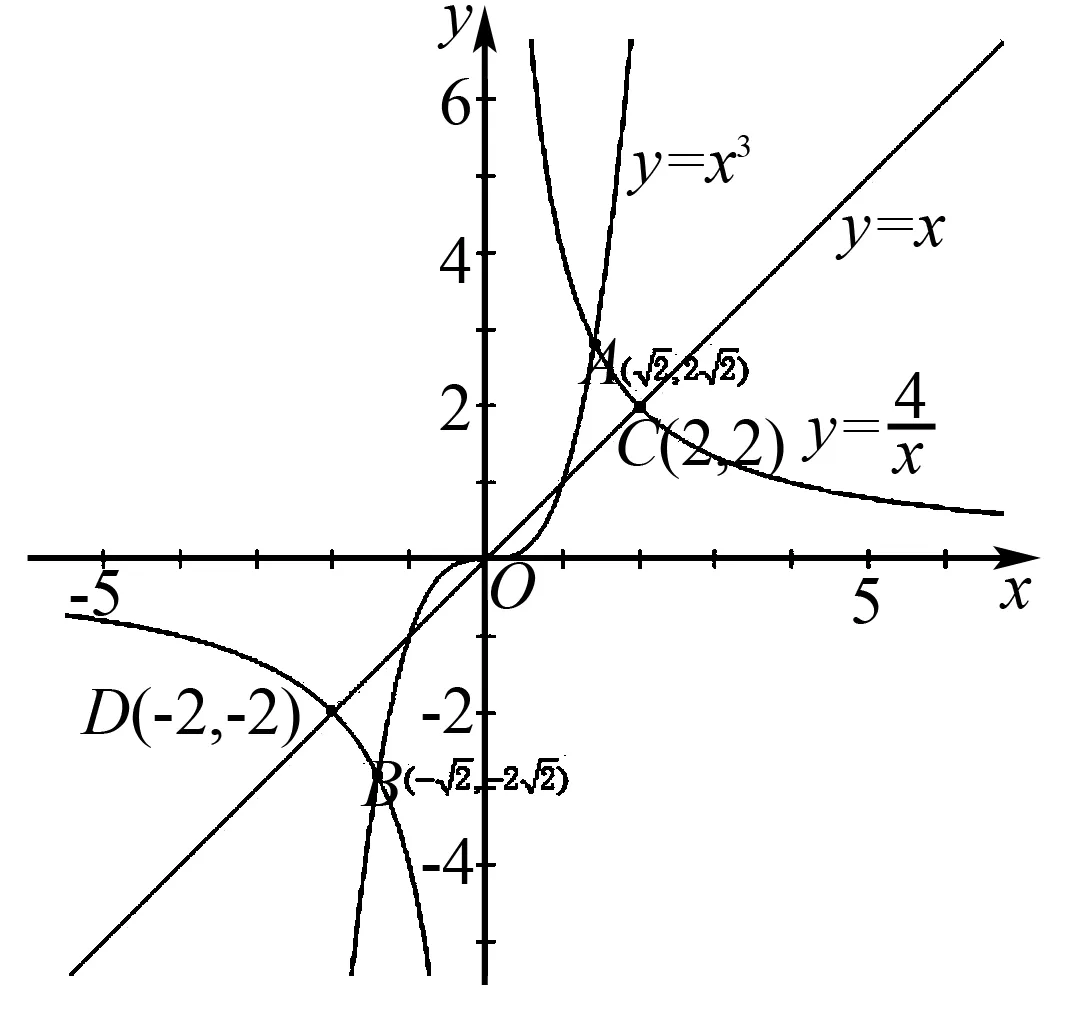
图1

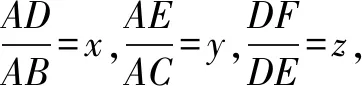
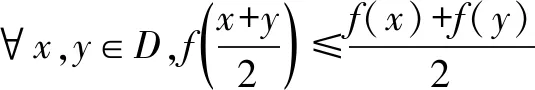
A.f(x)=2xB.f(x)=x3

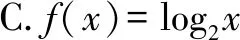
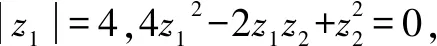
13.已知实数a,b满足4a2-5ab+4b2=19，求a2+b2的最大值.

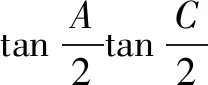
15.已知a1=7；当n≥2时，an表示7n的末两位数字之和.求a1+a2+a3+…+a2019.

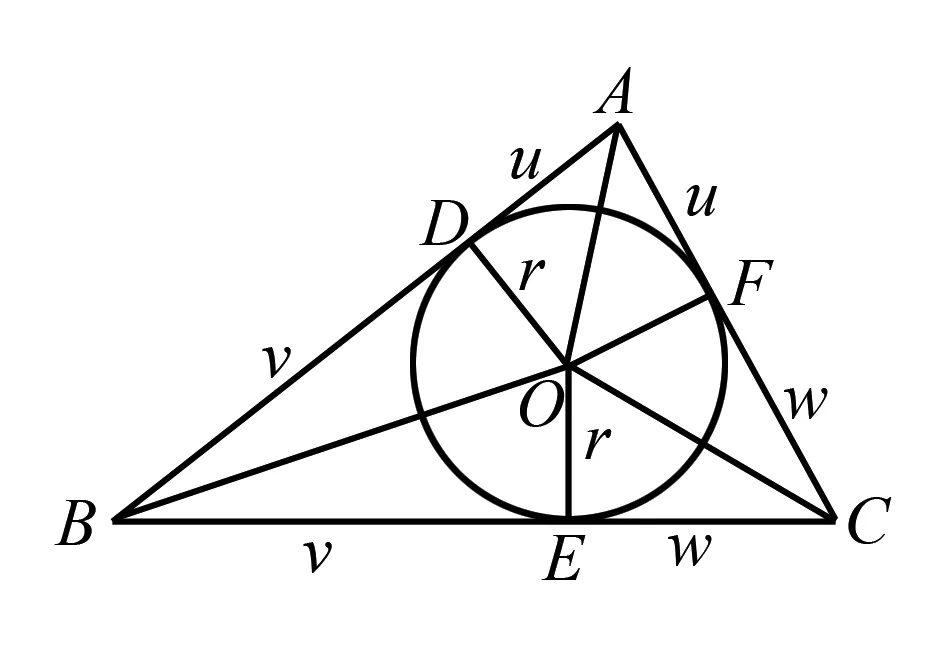
16.已知锐角△ABC的外接圆的圆心为O，点O到直线BC,CA,AB的距离分别为k,m,n.若BC=a,CA=b,AB=c，则k∶m∶n=( ).

C.sinA∶sinB∶sinCD.cosA∶cosB∶cosC

17.定义平面上的两点(m,n),(a,b)的折线距离d=|m-a|+|n-b|.若坐标平面上的点P到六个点(-1,2),(3,1),(3,5),(-2,4),(4,4),(6,6)的折线距离之和最小，则点P的坐标为.

18.若集合A={(x,y)|y≥x2},B={(x,y)|x2+(y-a)2≤1}，则A∩B=B的充要条件是( ).

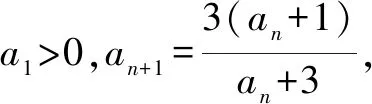
20.请写出命题“单调函数不是周期函数”的否命题、逆命题、逆否命题.

21.若C是以O为圆心、r为半径的圆周，两点P、P*在以O为起点的射线上，并且满足|OP|·|OP*|=r2，则称P、P*关于圆周C对称.那么，双曲线x2-y2=1上的点P(x,y)关于单位圆周C:x2+y2=1的对称点P*所满足的方程是( ).

A.x2-y2=x4+y4B.x2-y2=(x2+y2)2

C.x2-y2=2(x4+y4) D.x2-y2=2(x2+y2)2

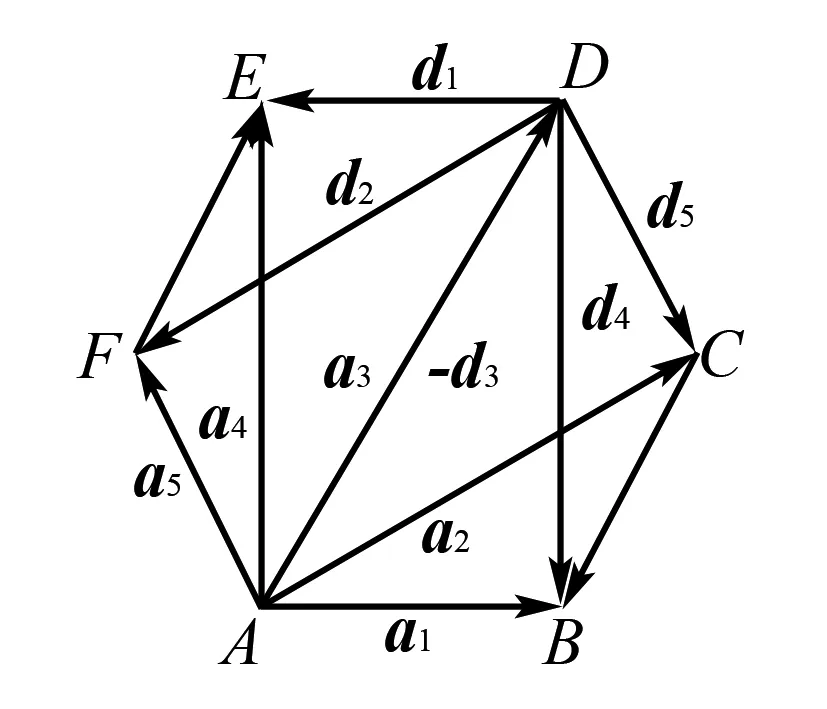
22.在边长为1的正六边形ABCDEF中，记以A为起点，其余顶点为终点的向量分别为a1,a2,a3,a4,a5；以D为起点，其余顶点为终点的向量分别为d1,d2,d3,d4,d5.若m,M分别为(ai+aj+ak)·(dr+ds+dt)的最小值与最大值，其中{i,j,k}⊆{1,2,3,4,5},{r,s,t}⊆{1,2,3,4,5}，则( ).

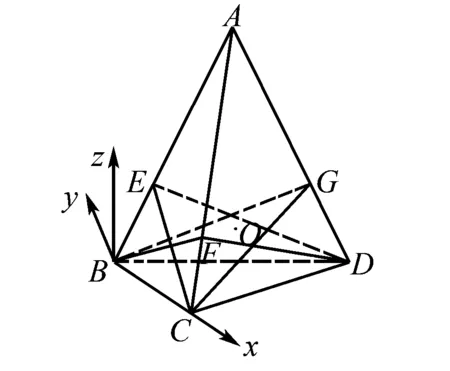
A.m=0,M>0 B.m<0,M>0

C.m<0,M=0 D.m<0,M<0

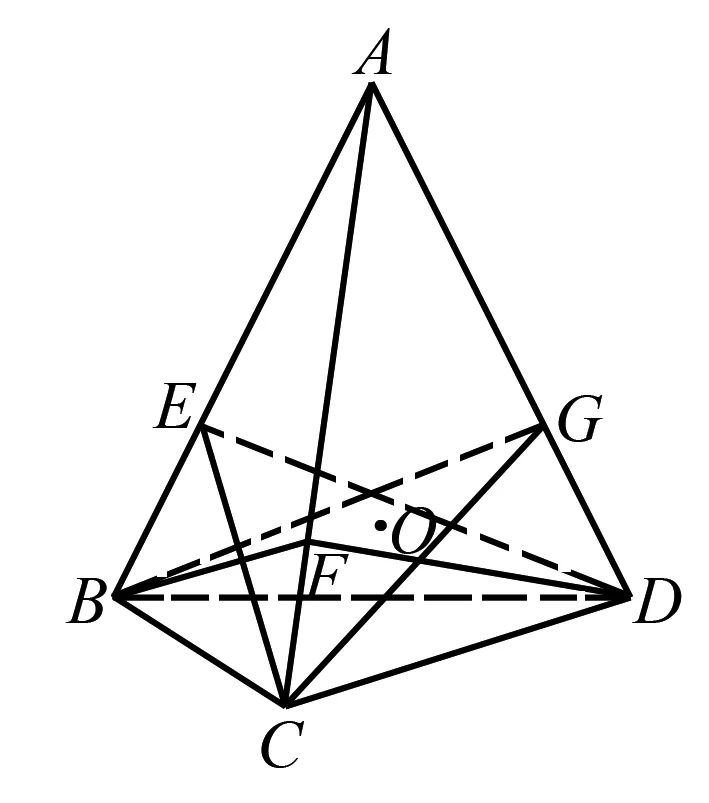
图2

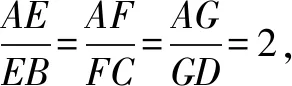
24.已知a>b>c,a+b+c=0，直线y=-bx与抛物线y=ax2+bx+c交于A,B两点.若点A,B在x轴上的射影分别为A1,B1，则当a,b,c变化时，|A1B1|的取值范围是( ).

25.已知集合A⊆{1,2,3,…,2000}，且集合A中的任意一个元素均不是另一个元素的5倍，求集合A的元素个数的最大值.

26.在与水平地面垂直的墙壁上挂有一幅矩形画，画的上、下边缘分别在观察者水平视线上方am和bm处.若要使观察者的视角最大，则观察者与墙壁的距离是( ).

参考答案

又因为lg(log310)=-lg(lg3)，所以

f(lg(log310))+f(lg(lg3))=5+f(lg(lg3))=8,

f(lg(lg3))=3.

注本题即2007年复旦大学千分考第75题.

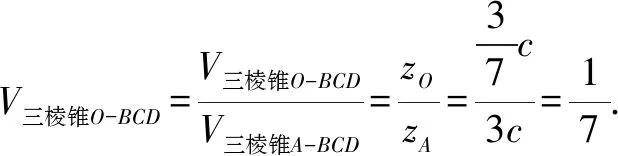
2.由题设，可得0logatanθ>0,x

再由0

注本题与2012年卓越联盟自主招生数学试题第3题实质相同，这道题是：

图3

综上所述，可得所求当a=0时，实数a的取值范围是(-∞,-6)∪(6,+∞).

即a<-6.

即a>6.

因而所求实数a的取值范围是(-∞,-6)∪(6,+∞).

注本题就是2008年高考上海卷理科第11题.

4.可设z=cosθ+isinθ(0≤θ<2π)，因而方程z2-2az+a2-a=0即

[(cosθ-a)2-sin2θ-a]+2isinθ(cosθ-a)=0，

(cosθ-a)2-sin2θ-a=sinθ(cosθ-a)=0。

进而可得下面的三种情形：

由题设可得它们均是正根，所以0

6.由题设，可得

再由题设，可得

n-m=m=3k(k∈N*).

所以n-m的最小值是3.

7.解法1 由题设及数学归纳法，可证得xn>0(n∈N*)，所以

若xn∈Z，可得3(n-4)/3∈N*，进而可得所求n的最小值是4.

解法2 由题设，可得

x3=(33-2/3)31/3=33-1/3,x3∉Z;x4=(33-1/3)31/3=1,x4∈Z.

因而所求n的最小值是4.

8.可得

所以

9.解法1 由均值不等式，可得

把它们相加后，可得

进而可得答案.

当x,y,z均是正数时：

x2+y2sin2θ≥2xysinθ(当且仅当x=ysinθ时取等号),

y2cos2θ+z2≥2yzcosθ(当且仅当ycosθ=z时取等号).

把它们相加，得

x2+y2+z2≥2(xysinθ+yzcosθ)(当且仅当x∶y∶z=sinθ∶1∶cosθ时取等号).

当x,y,z均是负数时，也可得上述结论成立.

所以由三元均值不等式，可得

注本题即2011年华约自主招生试题第9题，与2016年北京大学全国优秀中学生暑期夏令营数学试题第7题也实质相同.

11.A.由凸函数的定义可知，其图象下凸，进而可得答案.

12.由|z1|=4知，可设z1=4cosθ+4isinθ.

13.解法1由题设，可得

解法2由题设，可得

14.解法1 如图4所示，设△ABC的内切圆⊙O(其半径为r)与三边AB,BC,CA分别切于点D,E,F.由切线长定理，可设AD=AF=u,BD=BE=v,CE=CF=w.

图4

由海伦公式，可得

所以

解法2 由题设及正弦定理，可得

sinA+sinC=3sinB,

注本题即2010年华约自主招生试题第5题.

15.由7n+4-7n=7n(74-1)=100·24·7n，可得7n+4与7n的末两位数相同，这里n∈N*，约定71的末两位数是07即7.

进而可得{an}是周期数列且一个周期是4，还可得a1=7,a2=13,a3=7,a4=1，所以

a1+a2+a3+…+a2019+a2020=505(a1+a2+a3+a4)=505(7+13+7+1)=14140.

又因为a2020=a4=1，所以a1+a2+a3+…+a2019=14139.

16.D.设△ABC的外接圆半径为R，三边长分别为a,b,c，外心O到三边a,b,c的距离分别是k,m,n，可得2S△OAB=R2sin2C=cn=2RnsinC,n=RcosC，…所以k∶m∶n=cosA∶cosB∶cosC.

注对于任意△ABC，相应的结论是k∶m∶n=|cosA|∶|cosB|∶|cosC|.

证明如下：当C是钝角时，可得

2S△OAB=R2sin(2π-2C)=-R2sin2C

=-2R2sinCcosC=cn=2RncosC,

n=-RcosC=R|cosC|.

进而可得欲证结论成立.

本题即2012年北约自主招生数学试题第4题.

17.(3,4).设点P的坐标为(x,y)，可得点P到题中六个点的折线距离之和

L=(|x+2|+|x+1|+2|x-3|+|x-4|+|x-6|)+(|y-1|+|y-2|+2|y-4|+|y-5|+|y-6|).

由零点讨论法，可得

对于函数

f(x)=|x+2|+|x+1|+2|x-3|+|x-4|+|x-6|,

当且仅当x=3时，f(x)取到最小值.

对于函数

g(y)=|y-1|+|y-2|+2|y-4|+|y-5|+|y-6|,

当且仅当y=4时，g(y)取到最小值.

进而可得答案.

注本题与下面的一道高考题如出一辙：

(2009上海高考理科第13题)某地街道呈现东—西、南—北向的网格状，相邻街距都为1.两街道相交的点称为格点.若以互相垂直的两条街道为轴建立直角坐标系，现有下述格点(-2，2)，(3，1)，(3，4)，(-2，3)，(4，5)，(6，6)为报刊零售点.请确定一个格点(除零售点外)____为发行站，使6个零售点沿街道到发行站之间路程的和最短.(答案：(3,3).)

18.B.通过画图可知，题设即B⊆A，也即圆x2+(y-a)2=1在抛物线y=x2内(抛物线内指含焦点的区域，因而a≥1).

进而可得题设即抛物线y=x2上的任意一点(t,t2)均不在圆x2+(y-a)2=1内，也即t2+(t2-a)2≥1(t∈R),

19.解法1 可先用数学归纳法证得an>0(n∈N*)，因而

解法2 可先用数学归纳法证得an>0(n∈N*)，进而可得题设中的递推式即

再由an>0(n∈N*)，可得

20.逆命题：若一个函数不是周期函数，则它是单调函数；

否命题：若一个函数不单调，则它是周期函数；

逆否命题：若一个函数是周期函数，则它不是单调函数.

令x=x0t,y=y0t,得

x2-y2=(x2+y2)2.

此即点Pn的轨迹方程.

注本题即2010年复旦大学千分考第140题.

22.D.如图5所示，线段AD是正六边形ABCDEF的主对角线.

图5

在所有的ap·dq(p,q∈{1,2,3,4,5})中，只有a1·d5与a5·d1为正数，且在所有的|ap·dq|(p,q∈{1,2,3,4,5})中，最小的是|a1·d5|与|a5·d1|，所以(ai+aj+ak)·(dr+ds+dt)的展开式的9项之和是负数，所以题中的最大值M<0，进而可得答案是D.

23.C.如图6所示建立空间直角坐标系B-xyz，其中点C在x轴的正半轴上，点D在坐标平面xOy内.

图6

可设A(3a,3b,3c)(c>0),C(3d,0,0)(d>0),D(3e,3f,0)，进而可得E(a,b,c),F(a+2d,b,c),G(a+2e,b+2f,c)，再求得平面BCG,CDE,DBF的方程分别是cy-(b+2f)z=0,cfx+c(d-e)y+(be+3df-af-bd)z-3cdf=0，cfx-cey+(be-af-2df)z=0.