侧渠底高对分水口水力特性影响数值模拟研究

王文娥，刘海强，胡笑涛

·农业水土工程·

侧渠底高对分水口水力特性影响数值模拟研究

王文娥，刘海强，胡笑涛

（西北农林科技大学旱区农业水土工程教育部重点实验室，杨凌 712100）

目前对灌区分水口水力性能的研究多集中在主渠和侧渠底部高程相等的情况下，对于普遍存在的侧渠底部高程高于主渠时的分流特性缺乏系统研究。该文在试验基础上，利用FLOW-3D软件对侧渠不同底高、主渠来流量的矩形渠道分水口进行了数值模拟研究，将主渠各断面水深、流速的模拟值与实测值进行对比，发现流速变化与实测值变化规律基本一致，相对误差均小于10%，利用FLOW-3D对分水口进行数值计算具有合理可信性。结果表明：分水口处的水面波动受主渠来流的影响，流量越大，波动越大；高于侧渠底高的水流会对低于侧渠底高的下层水流产生影响，使下层水流具有向上的流速分量，参与分水口分流；同一主渠来流量下，随侧渠底高的增加，侧渠进口断面最大流速和水深逐渐减小；侧渠进口断面靠近上游端的区域湍动较大，而在下游端靠近底部湍动能值较小。研究为灌区配水及水量控制提供了参考依据。

数值分析；流量；流速；矩形渠道；分水口；渠宽比

0 引 言

灌区渠道量水是实现灌区现代化的重要途径[1]，分水口是灌区灌溉渠系常见的过水建筑物[2-3]，为方便灌溉，通常直接在经过田间的渠道一侧开设分水口引水入田。若直接在分水口处进行量水，就可获得进入田间的流量，同时避免因修建特设量水设施造成的二次水头损失。对于分水口的水力性能的研究，最初是理论分析与试验相结合进行研究。Taylor等[4-7]分别研究了分水口处的分流规律，Hsu等[8-9]研究了矩形渠道主侧渠道等宽时的分水规律，建立了主渠上下游水深比、流量比与傅汝德数关系等一维理论模型。Hayes等[10-13]利用湍流模型对明渠分水口处的流场变化进行了二维分析研究。Neary等[14-15]选用湍流模型对渠道分流问题进行了三维数值模型模拟，数值模拟结果与试验数据的对比结果表明，两者平均速度变化趋势之间存在一定的对应关系。Huang等[16]根据汇流试验数据和数值模拟数据验证了基于Reynolds-Averaged NavierStokes方程和湍流模型的三维数值模型。近年来，随着计算机的广泛应用及CFD理论的发展和完善，数值模拟技术开始广泛应用到渠道量水方面。杨帆等[17-18]利用FLUENT软件对取水角为45°和30°的明渠岸边侧向取水口进行了三维数值模拟，分析了分水口处的流速分布、分水宽度及湍动能。孟文等[19-21]利用FLOW-3D软件对弯道及明渠分水口水流进行了数值模拟，分析了分水口水力特性的变化规律和影响因素。

在对分水口的数值模拟研究中，大多数研究主要针对主渠与侧渠底部高程一致的情况下进行模拟，对侧渠底部高程高于主渠时的分水特性还缺少深入系统地研究。分水口处的流场分布复杂，试验方法可以测定一定数量的断面流速、水深数据，采用数值模拟的方法可以更全面了解分水口附近的流场分布，为系统分析分水口水力性能提供全面的流场分布资料。本文基于矩形渠道分水口水力性能试验研究，利用FLOW-3D软件对不同侧渠底高的分水口进行了数值模拟计算，并将模拟结果与试验结果进行对比，以期深入了解侧渠底高对分水口处水流特性的影响，为灌区配水及水量控制提供依据。

1 数学模型与试验设置

1.1 控制方程

分水口水流流动控制方程包括连续性方程、运动方程及湍流方程[12]。

连续性方程

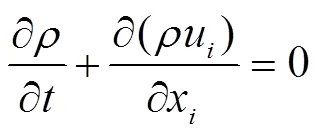
运动方程

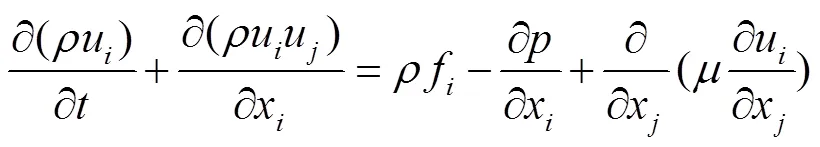
式中为流体密度，研究对象为水，取值1 000 kg/m3；为流动时间，s；u、u分别为流速矢量在x、x方向的分量（=1,2,3；=1,2,3），m/s；为流体动力黏滞系数，kg·/(m·s)；为流体压强，Pa；f为流体所受的质量力，m/s2。

1.2 RNG k-ε模型

灌区输水渠道及末级渠道中雷诺数均大于2 000，渠道中的水流基本都属于紊流粗糙区（阻力平方区），本文研究的渠道尺寸接近灌区农渠及毛渠，渠道分水口处的水流状态为湍流，所以选用湍流模型[22]。目前常用的3种-湍流模型中，RNG模型是基于重整化群（renormalization group）的理论提出来的[23]，经过对标准湍流模型的改进和实用化处理，RNG模型考虑了旋转效应，因此提高了强旋转流动计算精度。水流流经分水口后，一部分水流流向下游，而另一部分通过分水口流向侧渠，因此分水口处的水流变化强烈，呈现复杂的三维特性，故选用RNG模型。对于不可压缩流体流动，其相应的和方程[23]为

方程

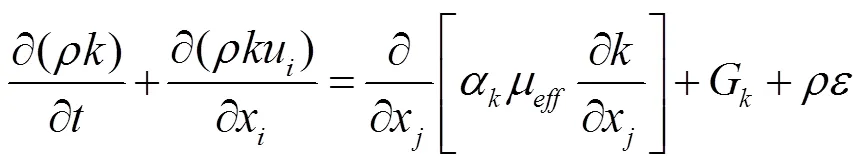
方程

1.3 TruVOF模型

目前，大部分处理水气两相流的自由表面都是采用流体体积法[24]，该方法往往会增加计算时间或是计算结果有较大偏差，FLOW-3D软件采用了TruVOF方法，只计算含有液体单元，因此在很大程度上减少了模型收敛所需的时间，同时精确模拟具有自由界面的流动问题[22]。TruVOF法对流体界面的三维重构控制方程[17]为

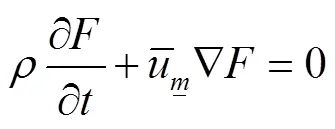
1.4 验证试验布置

为了验证数值分析模型及模拟结果，首先进行了原型试验，在西北农林科技大学水工厅进行，试验系统的平面布置如图1a所示。试验系统由水泵、供水管道、蓄水池、稳水池、矩形渠道、排水池及回水管道组成。试验中主渠和侧渠均为矩形渠道，主渠长12 m，宽0.46 m，侧渠长2.5 m，宽度在0.14～0.46 m范围可调，侧渠较主渠底部高程分别高出0.06、0.08、0.1 m。共设置8个测流断面，断面测点具体布置如图1b所示，距分水口上游端和下游端0.5 m处设断面Ⅰ和Ⅶ，试验中侧渠宽度值非定值，为了更好地分析主渠在分水口处水面变化规律，在分水口处共设置5个断面，分别为断面Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ，各断面间隔相同，每个断面设置3个测点，位于主渠中心处（）、距主渠边壁5 cm处（和，其中主渠无分水口一侧，为靠近分水口一侧）。使用SCM60型水位测针测量，精度±0.1 mm。

注：a、b、c分别主渠无分水口一侧、主渠中心处、靠近分水口一侧；Q为主渠来流量，L·s-1。Ⅰ到Ⅷ分别为各测点所在断面。

为了更好地对比分析模拟结果与试验结果，同时消除边界条件的影响，本研究对试验渠道进行了简化，如图2所示。模拟主、侧渠宽度跟实际主、侧渠宽度B、b一致，主渠道为0.46 m，侧渠道分别设置了0.14、0.22、0.30、0.38、0.46 cm，即主侧渠宽比R（R=b/B）为0.3、0.48、0.65、0.83、1；侧渠底高（以主渠底部高程为0点）取0.06、0.08、0.1 m，主渠和侧渠长度在实际渠道长度基础上相应的延伸，分别取12和5 m。分水口附近流场变化剧烈，因此对分水口处的网格进行了加密，单元格长度为0.01 m，其余区域单元网格为0.02 m，网格总量约为90万。渠道模型中主渠进口边界设定为流量进口（volume flow rate），进口流量与试验相同，分别为19.96、25.2、30.2、36.5、45.32 L/s；主渠、侧渠末端出口设为自由出流（outflow）；渠道边壁选择无滑移固壁边壁（wall）；自由水面以上为空气，相对压强为0。

图2 体型图及边界设置

2 结果与分析

2.1 模型验证

为了更好地将数学模型计算水深与实测水深进行对比，主渠断面选取与试验位置相同（图1b），模型区域坐标原点取在主渠进口渠底，方向为侧渠水流流向，方向为主渠水流方向，方向垂直向上。

根据矩形渠道分水口试验和数值模拟结果，对主渠各个来流量、不同侧渠底高下的分水口各断面水深进行了对比分析，表1和表2分别为主渠来流量为30.2 L/s、渠宽比为1时各侧渠底高条件下，以及主渠来流量为45.32 L/s、侧渠底高0.06 m时5种渠宽比的模型计算结果与试验结果的对比分析结果。

从表1和表2中可以看出，模拟值与实测值相差较小，主渠无分水口侧处的相对误差值最大为8.76%，主渠中心线处的相对误差值最大为8.58%，主渠靠近分水口侧处的相对误差值最大为8.45%，相对误差值都在9%以内，表明利用FLOW-3D对矩形渠道分水口的模拟水深结果可信。

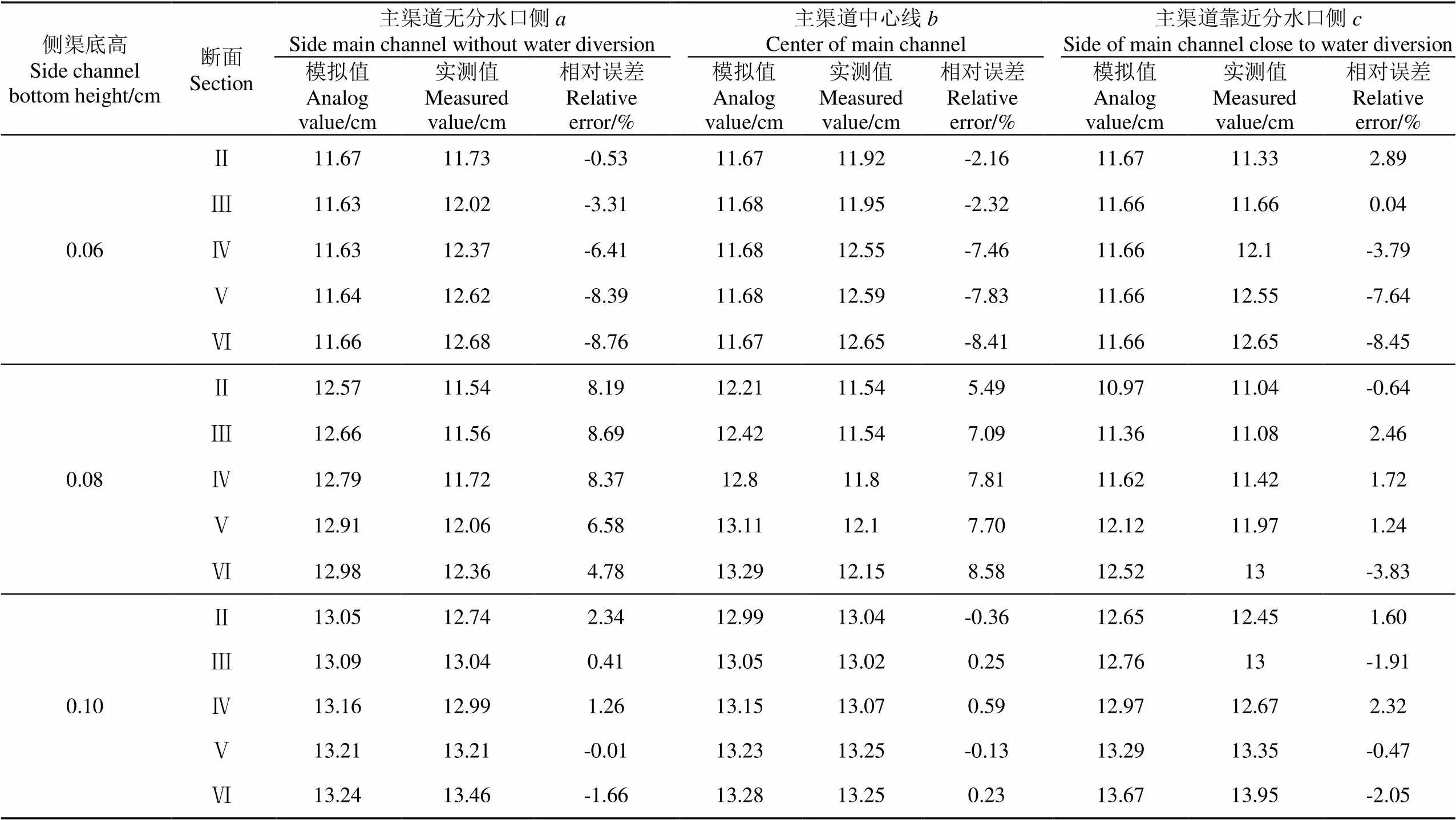
表1 来流量30.2 L·s-1和渠宽比1时不同断面水深相对误差分析

注：相对误差=（模拟值−实测值）/实测值×100%，下同。

Note: Relative error = (analog value-measured value)/measured value×100%, same as below.

流速是分析分水口处水流水力性能和运动规律的基本要素。为了保证利用数值模拟研究分水口处流速分布的合理性，以流量45.32 L/s、侧渠底高为0.06 m、渠宽比为1时为例，对断面Ⅰ、断面Ⅱ和断面Ⅶ和距分水口1 m处的侧渠断面流速模拟值和实测值进行了比较，在流量45.32 L/s时，主渠和侧渠水深分别小于0.15和0.09 m，因此提取了主渠各断面测点分别在0.4和0.7处（为主渠流量45.32 L/s时断面Ⅰ的水深，m）、侧渠各断面0.5处的流速。由图3a～图3d可知，各断面流速实测值与模拟值分布规律相似，且模拟值与实测值的最大相对误差均在10%以内，表明利用FLOW-3D对分水口进行流速研究和分析合理可信。

同一来流量和侧渠底高、渠宽比不同时分水口附近水面线、流速分布变化趋势一致[25]，本文主要讨论侧渠底高对分水口水力性能的影响，因此以渠宽比=1时分水口附近流场分布为例，分析侧渠底高对分水口水力特性的影响。

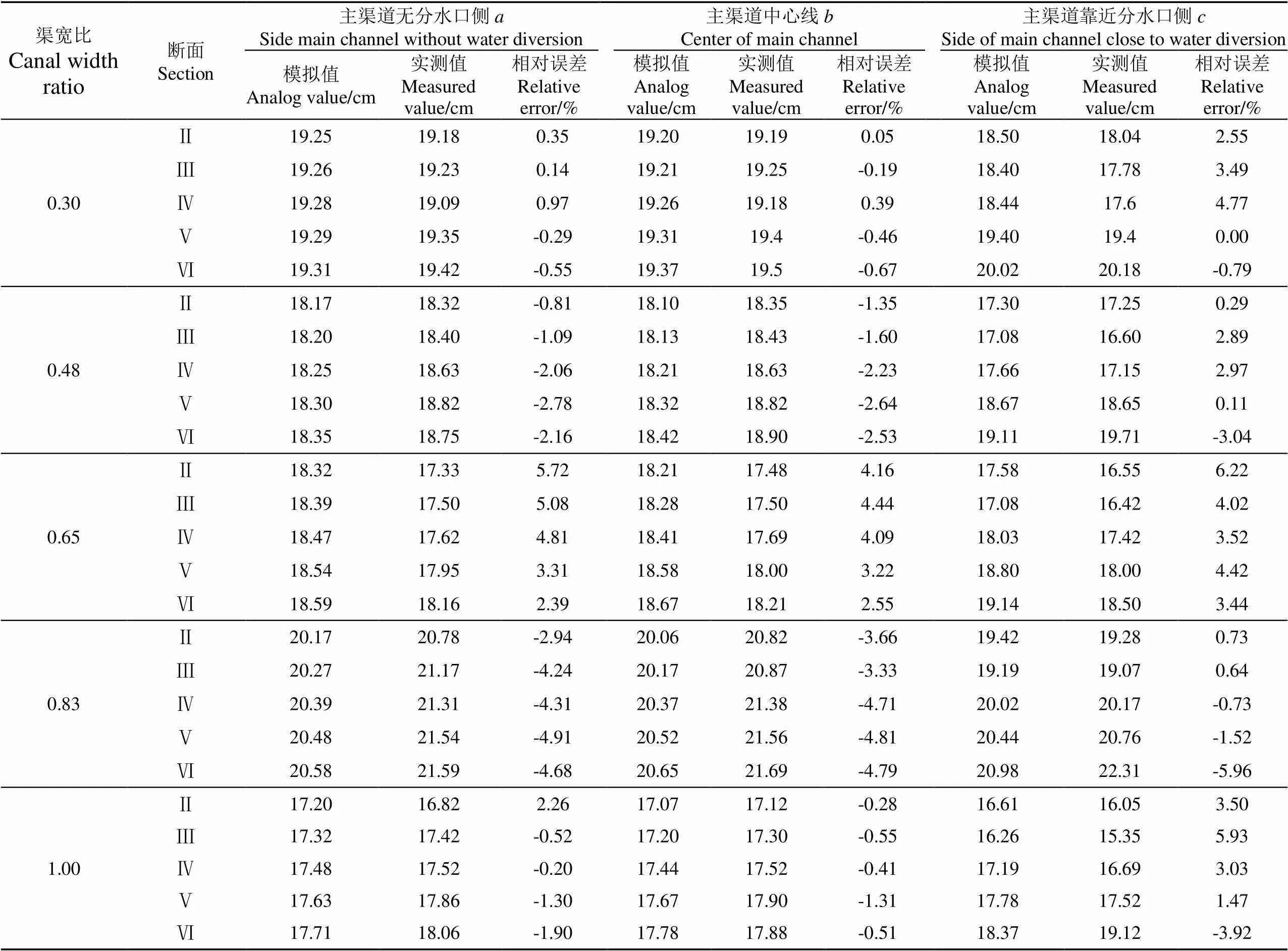
表2 来流量45.32L·s-1和侧渠底高0.06 m时各渠宽比下断面水深相对误差

注：H为主渠流量45.32 L·s-1时断面Ⅰ的水深，m。

2.2 模拟结果

2.2.1 水面线

主渠水流在分水口处，受到分流的影响，水面变化剧烈，具有复杂的三维特性[19]，如图4a所示。为了研究分水口处的水面变化，提取了模拟结果中的水深。受篇幅所限，而且各侧渠底高下的主渠在分水口处的水面变化规律基本相似，图4b给出了侧渠底高为0.06 m时不同来流量下的主渠在分水口处的水面线变化图。由图4b可以看出，主渠远离分水口一侧、主渠中心线和主渠靠近分水口一侧的水面线变化各不相同。水流靠近分水口时，和处水深呈现逐渐上升的趋势，随主渠来流量的增大，上升趋势逐渐增加，当主渠来流量较小时，和处水面线基本重合，当流量较大时，处水面要低于处水面，即越靠近分水口，水面受分水口的影响越大；而处水深在分水口段呈先减小后增加的趋势，水深最小点的位置随主渠来流量的变化而变化，水深在分水口下游端达到最大值，且最大值得位置点保持不变；当主渠来流量较小时，、和处的水面波动较小，尤其是和处水面线近似于直线，当主渠来流量增加时，三处的水面波动程度增加，处的水面波动最大，主渠来流量越大，分水口处的水深变化越剧烈，水面越不稳定。

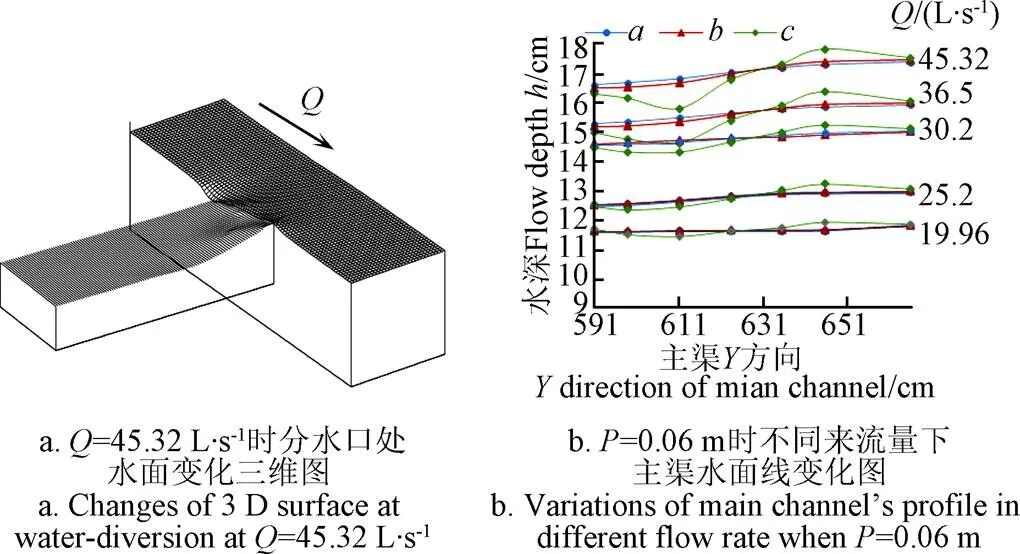
注：Q为主渠来流量，L·s-1；P为侧渠底高，m。

2.2.2 主渠断面流速

主渠水流流经分水口时，受分水口的影响，主渠各层流线急剧变化，各断面流速分布不同，故提取了数值模拟结果中不同水深处的流速矢量图以及各断面不同水深处的流速。图5为流量为45.32 L/s，侧渠底高为0.06 m，水深分别为0.5、、1.5、2下的流速矢量分布图。

注：流量为45.32 L·s-1；侧渠底高0.06 m。图6~图7同。

由图5可以看出，当主渠中水流未流经分水口时，水流不受分水口的影响，流线较为平顺，流速分布均匀；当水流运动到距分水口上游端一定距离时，受到分水口的影响，主渠在靠近分水口一侧的流线发生偏转，而远离分水口处的流线偏转角度较小，且随着距离的增加，偏转角度逐渐减小，即分水口对主渠水流的影响随着距离的增加逐渐减小；主渠水流流经分水口时，受到水流侧向离心力的影响，部分水流流线发生偏折，进入侧渠。当主渠水深小于侧渠底高时，侧渠未分流，主渠水流流线将不受分水口的影响，流线较为平顺，当侧渠分流时，由图5a和图5b可以看出，分水口处的流线较主渠上游端发生了明显的偏转，说明高于侧渠底高的水流即参与分流的水流对下层水流产生了影响，使低于侧渠底高下的部分水流产生了趋向于侧渠的流动趋势。

为了更好地了解主渠各断面不同水深处各方向流速和大小变化，分析了各工况下的流速。图6给出了流量为45.32 L/s，侧渠底高为0.06 m时0.5、、1.5、2水深下的主渠断面Ⅰ~Ⅶ的沿主渠方向（）、垂直于主渠方向（）和垂直于渠道方向（）流速分布。

从图6中可以看出各断面靠近渠道边壁的和方向的流速，受边壁影响，流速越靠近边壁值较小；在分水口处，水深高于侧渠底高时，水流不受侧渠底坎边壁的影响，和方向的流速随坐标的增加而增大；当坐标在0到2/3B范围内时，主渠方向流速值沿主渠方向逐渐减小；当坐标大于2/3B时，靠近分水口上游端的断面Ⅱ和断面Ⅲ方向流速高于断面Ⅰ，分水口下游端的断面Ⅵ方向流速越靠近分水口下游端值越小。由于远离分水口，断面Ⅰ和断面Ⅶ方向流速大致呈对称分布，且对称点随水深的增加逐渐远离分水口一侧，断面Ⅰ和断面Ⅶ位于分水口上下游一定距离处，分水口对断面Ⅰ和断面Ⅶ在方向的流速影响较小，但随水深的增加，各断面方向流速最大值逐渐增大，因为随着水深的增加，渠道底部边壁和底坎对水流的影响减小，流速逐渐增加；由图6a中垂直于主渠方向流失可知，分水口处的各断面（断面Ⅱ~Ⅵ）方向流速沿侧渠方向呈先增大后减小的规律，且流速最大值的点随断面的改变而改变，受侧渠进口处底坎的影响，方向流速在底坎处的速度骤减为0，受分水口侧向离心力的影响，越靠近分水口，影响越大，即流速变化越大，所以水深低于侧渠底高时，主渠各断面流速呈先增加后减小的趋势；图6b和图6c（主渠和垂直于主渠方向流速）中，水深高于底坎高度，不再受底坎的阻挡作用，断面Ⅲ、Ⅳ、Ⅴ流速值沿侧渠方向逐渐增加，断面Ⅱ、Ⅵ分别为分水口上、下游端，受到主渠垂向边壁的阻碍作用，流速值先增加后减小，且变化趋势较断面Ⅲ、Ⅳ、Ⅴ要小的多。从4个垂向流速图，可以看出方向流速在分水口处变化较大，越靠近分水口，流速值沿主渠方向变化越大；当水深低于侧渠底高高时，从图6a和图6b垂向流速图可以看出，分水口处的水流具有向上的方向流速，受上层水流分流的影响，低于侧渠底高的水流也参与分流，且越靠近分水口，方向流速值越大，参与分流量越多。

为了解主渠靠近分水口一侧各断面沿程流速变化，将各断面点不同水深下的流速值沿主渠方向绘制成流速变化图。图7为流量45.32 L/s，侧渠底高为0.06 m时主渠断面Ⅰ~Ⅶ点流速矢量图。由图7可以看出，各水深下分水口处方向流速越靠近分水口下游端，流速值越小，即方向流速值在分水口上游端（断面Ⅱ）达到最大值，在断面Ⅵ处流速值最小，过后流速值虽有增加但流速值仍小于主渠上游。各水深下方向流速值呈先增加后减小的变化，在断面Ⅵ处（即侧渠中心线）达到最大，距分水口越远，方向的流速越小，受分水口侧向分水的影响越小。各水深下方向流速在远离分水口的两个断面流速值接近于0，而分水口处的流速值呈先增加后减小的趋势，最大值点在断面Ⅳ，此时水深为侧渠底高；高于侧渠底高的水流在分水口处对下层水流产生了扰动，使低于侧渠底高的水流也参与上层分流，若主渠中含有泥沙，当底坎前的水流方向流速值大于渠道底部泥沙起动流速时，会携带泥沙进入侧渠；若方向流速值达不到泥沙起动流速，那么侧渠进口处的底坎就会具有阻碍泥沙进入侧渠的作用。

图6 主渠各断面流速矢量图

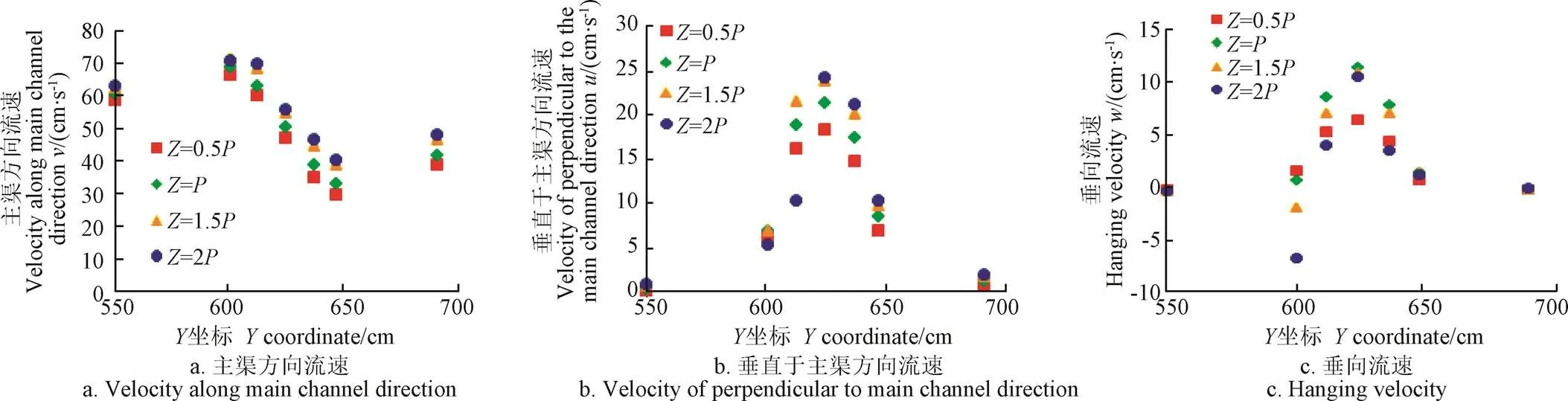
图7 主渠各断面c点流速(v)矢量图

2.2.3 侧渠进口断面流速

水流流经分水口时，在分水口处无侧向边壁的约束，主渠部分水流发生偏转进入侧渠，由于主渠水流具有沿主渠方向的流速，因此侧渠进口处的流速沿渠道断面方向变化。图8为流量为30.2 L/s，主渠下游自由出流工况下，各侧渠底高下侧渠进口断面流速分布图。由图8可以看出，水流进入侧渠后，受侧向分水的影响，水流在分水口上游端与边壁分离，而在分水口下游端水流碰撞边壁，流速逐渐减小；侧渠进口断面越靠近上游端，水深和沿侧渠方向流速越小，随坐标的增加水深逐渐增加，在断面下游端达到最大值；各水深沿侧渠方向流速值最大点随水深的增加逐渐靠近侧渠中心，断面纵向流速等值线向下游倾斜；同一主渠来流量下，堰坎高度越大，侧渠进口断面同一位置处的水深越小，同时水面沿断面变化越小；随侧渠底高的增加，侧渠进口断面最大流速和水深逐渐减小。

图8 不同侧渠底高下侧渠进口断面流速分布图

2.2.4 湍动能

湍动能是表征湍流脉动剧烈程度的重要参量[26]，脉动对于输水挟沙有着重要的影响，会增加水流与边壁的碰撞，侵蚀边壁，增加水头损失。分水口处水流各流层之间液体质点相互混掺，所以属于湍流流动。图9为流量45.32 L/s、侧渠底高0.06 m时的主渠在分水口处断面和侧渠进口断面湍动能等值线图。

分水口处的水流受到侧向分水、固体边壁的双重影响，存在着分流、潜流和滞流等多种流动现象，为高湍动区。从图中可以看出，在远离分水口接近表层处，各断面湍动强度值较大（图9a～图9e左侧上部）；结合图6可以看出，主渠道来流在经过分水口时，靠近分水口处的水流进入侧渠道；远离分水口一侧水流也受到影响，水流流线与边壁发生分离，流速方向和大小变化剧烈，湍动强度较大（图9a～图9e右侧下部）。湍动强度值越靠近分水口（侧渠道进口）处越大，即水流紊动越剧烈，流速变化越快；图9f为侧渠道进口断面湍动能分布图，在分水口上游端，水流在此处发生偏转进入侧渠道，由于水流具有沿主渠道方向的流速，在发生偏转时水流会脱离边壁，同时在侧渠道进口处形成回流区，流速变化较大，易形成涡流，所以靠近分水口上游端的区域湍动能值较大，在分水口下游端湍动能值较小，实际运行中将对泥沙淤积的位置及数量产生影响。

图9 Q=45.32 L·s-1、P=0.06 m时各断面湍动能分布图

3 结 论

灌区渠道量水是实现灌区现代化的重要途径，利用渠系分水口进行流量测量，可避免由于增设量水设施引起的二次水头损失；目前对于主渠与侧渠底部高程不相同的情况还缺乏深入系统地研究。本文通过试验和FLOW-3D软件对不同侧渠底高的矩形渠道分水口水力性能进行了模拟研究，分析了分水口处主渠水面线变化、分水口处各断面流速分布及分水口处湍动能分布，得到了以下结论：

1）采用RNG模型对矩形分水口进行数值模拟计算，模拟水深和流速与实测值相对误差均在10%以内，流速变化与实测值变化规律基本一致。

2）主渠在分水口处的水面线波动较为剧烈，越靠近分水口，水面线波动越剧烈；在分水口下游端水深达到最大值。当主渠来流量增加时，分水口处的水面波动程度增加，主渠来流量越大，分水口处的水深变化越剧烈，水面越不稳定。

3）主渠各断面流速分布规律在不同水深下大致相同，各断面方向流速分布较为均匀，靠近边壁处，流速较小；高于侧渠底高的主渠水流对下层分流产生扰动，使沿主渠流动的水流发生趋向于侧渠的流动趋势，侧渠底坎前的水流具有向上的流速，与上层水流一起参与分流。

4）侧渠进口断面不同水深下沿侧渠方向流速值最大点随水深的增加逐渐靠近侧渠中心，断面纵向流速等值线向下游倾斜；同一主渠来流量下，侧渠底高越大，侧渠进口断面同一位置处的水深越小，同时水面沿断面变化越小。

5）湍动强度值越靠近分水口（侧渠进口）处湍动值较大；在远离分水口接近表层处，各断面湍动强度值较大，受到边壁和分水口的影响，湍动强度较大，流速变化剧烈；侧渠进口断面靠近分水口上游端的区域湍动能值较大，在分水口下游端湍动能值较小。

分水口处的水力特性还受渠宽比、主渠与侧渠轴线夹角、分水口结构、水流中的泥沙含量等因素影响，还需进一步系统研究，确定各因素对分流特性的影响。

[1] 许迪，龚时宏. 大型灌区节水改造技术支撑体系及研究重点[J]. 水利学报，2007，38(7)：806－811.

Xu Di, Gong Shihong. Technical supporting system for water saving orientated rehabilitation of large irrigation districts[J]. Journal of Hydraulic Engineering. 2007, 38(7): 806－811. (in Chinese with English abstract)

[2] 张成，郑立松，黄成涛，等. 大型输水渠道分水口分水影响及调控原则研究[J]. 应用基础与工程科学学报，2012，20(6)：975－986.

Zhang Cheng, Zheng Lisong, Huang Chengtao, et al. Influence and principle of water division operation of flow diversion gate in large water transfer channel[J]. Journal of Basic Science and Engineering, 2012, 20(6): 975－986. (in Chinese with English abstract)

[3] 曹继文，陈惠泉，贺益英. 明渠岸边横向取水口水力特性的试验研究[J]. 水利学报，2003，34(10)：32－37.

Cao Jiwen, Chen Huiquan, He Yiying. Experimental study on hydraulic characteristics of lateral intake in open channel[J]. Journal of Hydraulic Engineering, 2003, 34(10): 32－37. (in Chinese with English abstract)

[4] Taylor E H. Flow characteristics at rectangular open-channel junctions[J]. Transactions of the American Society of Civil Engineers, 1944, 109(1): 893－912.

[5] Law S W, Reynolds A J. Dividing flow in an open channel[J]. Journal of the Hydraulics Division, 1965, 92(2): 207－231.

[6] Ramamurthy A S, Satish M G. Division of flow in short open channel branches[J]. Journal of Hydraulic Engineering, 1988, 114(4): 428－438.

[7] Kesserwani G, Vazquez J, Rivière N, et al. New approach for predicting flow bifurcation at right-angled open-channel Junction[J]. Journal of Hydraulic Engineering, 2010, 136(9): 662－668.

[8] Hsu C C, Tang C J, Lee W J, et al. Subcritical 90° equal-width open-channel dividing flow[J]. Journal of Hydraulic Engineering, 2002, 128(7): 716－720.

[9] Barkdoll B D. Discussion of “Subcritical 90° equal-width open-channel dividing flow” by Chung-Chieh Hsu, Chii-Jau Tang, Wen-Jung Lee, and Mon-Yi Shieh[J]. Journal of Hydraulic Engineering, 2004, 130(2): 171－172.

[10] Hayes R E, Nandakumar K, Nasr-El-Din H. Steady laminar flow in a 90 degree planar branch[J]. Computers & Fluids, 1989, 17(4): 537－553.

[11] Haider S, Gabriel H F, Khan S A. Supercritical flow simulation at a right channel junction. Comparison between a uniform and a sparse mesh[J]. Ksce Journal of Civil Engineering, 2017, 21(7): 2984－2990.

[12] Shettar A S, Murthy K K. A numerical study of division of flow in open channels[J]. Journal of Hydraulic Research, 1996, 34(5): 651－675.

[13] Bramley J S, Dennis S C R. The numerical solution of two-dimensional flow in a branching channel[J]. Computers & Fluids, 1984, 12(4): 339－355.

[14] Neary V S, Sotiropoulos F, Odgaard A J. Three dimensional numerical model of lateral intake inflows[J]. Journal of Hydraulic Engineering, 1999, 125(2): 126－138.

[15] Neary V S, Sotiropoulos F. Numerical investigation of laminar flows through 90-degree diversions of rectangular cross-section[J]. Computers & Fluids, 1996, 25(2): 95－118.

[16] Huang J, Weber L J, Lai Y G. Three-dimensional numerical study of flows in open-channel junctions[J]. Journal of Hydraulic Engineering, 2002, 128(3): 268－280.

[17] 杨帆，陈惠泉，郭军. 明渠岸边侧向45°取水口的水力特性试验研究[J]. 中国水利水电科学研究院学报，2006，4(4)：264－270.

Yang Fan, Chen Huiquan, Guo Jun. Experimental study on hydraulic characteristics of 45° lateral intake flow in open channel[J]. Journal of China Institute of Water Resources and Hydropower Research, 2006, 4(4): 264－270. (in Chinese with English abstract)

[18] 杨帆. 明渠岸边侧向取水的“取水角效应”研究[D]. 北京：中国水利水电科学研究院，2007.

Yang Fan. Study on “Diversion Angle Effect” of Lateral Intake Flow[D]. Beijing: China Institute of Water Resources and Hydropower Research, 2007. (in Chinese with English abstract)

[19] 孟文，孙宏伟，蒋俊峰. 分流对弯道分流口门分布的影响[J]. 农业科技与装备，2014，241(7)：59－63.

Meng Wen, Sun Hongwei, Jiang Junfeng. Effect of the surface velocity distribution at the entrance of the bend shunt[J]. Agricultural Science & Technology and Equipment, 2014, 241(7): 59－63. (in Chinese with English abstract)

[20] 郭维东，刘健，韩冬. 分流对弯道水流水力特性的影响[J]. 人民黄河，2009，31(6)：93－94.

Guo Weidong, Liu Jian, Han Dong. The influence of shunt on hydraulic characteristics of bend flow[J]. Yellow River, 2009, 31(6): 93－94. (in Chinese with English abstract)

[21] 李涛，邹健，曲少军，等. 基于不同断面形态的直角分流口处局部损失研究[J]. 水力发电学报，2017，36(6)：30－37.

Li Tao, Zou Jian, Qu Shaojun, et al. Local head loss of 90° lateral diversion from open channels of different cross-sectional shapes[J]. Journal of Hydroelectric Engineering, 2017, 36(6): 30－37. (in Chinese with English abstract)

[22] 王莹莹，王文娥，胡笑涛. 矩形渠道薄壁侧堰水力特性试验及数值模拟[J]. 水力发电学报，2016，35(1)：70－78.

Wang Yingying, Wang Wene, Hu Xiaotao. Experimental and numerical studies on hydraulic characteristic of sharp-crested weirs in rectangular channels[J]. Journal of Hydroelectric Engineering, 2016, 35(1): 70－78. (in Chinese with English abstract)

[23] 王福军. 计算流体动力学分析：CFD软件原理与应用[M]. 北京：清华大学出版社，2004.

[24] Hirt C W, Nichols B D. Volume of fluid (VOF) method for dynamics of free boundaries[J]. The Physics of Fluids, 1981, 39(1): 201－225.

[25] 刘海强，王文娥，胡笑涛. 矩形渠道分水口水力性能试验研究[J]. 排灌机械工程学报，2018，36(10)：1012－1016.

Liu Haiqiang, Wang Wene, Hu Xiaotao. Experimental study on hydraulic characteristics of rectangular water-diversion [J]. Journal of Drainage and Irrigation Machinery Engineering, 2018, 36(10): 1012－1016. (in Chinese with English abstract)

[26] 吕宏兴，裴国霞，杨玲霞. 水力学[M]. 北京：中国农业出版社，2002.

Numerical simulation of influence of side channel bottom height on hydraulic performance of bleeder

Wang Wen’e, Liu Haiqiang, Hu Xiaotao

(,,,712100,)

In recent years, most researches focus on the same height at the bottom of both main and side canal to study the hydraulic performance of water diversion. However, in practice, the height of main and side canal bottom are different in most irrigation districts. In this paper, the effect of the height of the side canal bottom on the hydraulic performance of bleeder was studied. The prototype test was carried out in Northwest A & F University in Yangling, Shannxi of China. In the prototype test, both the main channel and side channel were rectangular. The length of the main channel was 12-m long and 0.46-m wide. The length of the side channel was 2.5 m, and the width was adjustable in the range of 0.14-0.46 m. The elevation of the side channel was 0.06, 0.08 and 0.1 m higher than the bottom elevation of the main channel. A total of 8 flow sections were set up, 5 of which were at the water inlet. In order to analyze the water surface variation at the water diversion of the main channel, 3 measuring points at section I, section II, section III, section IV, section V, section VI were taken. The 3 measuring points were on the center line and 5 cm away from the wall of the main channel on both sides. The variables in the test were the side channel width and the flow rate. The water depth and velocity were determined at the measuring point. To eliminate the influence of boundary conditions, this study simplified the experimental channels. The width of the simulated main and side channels was the same as the actual width of the main and side channels. However, the lengths of the main and side channels were correspondingly extended on the basis of the actual channel length, which were 12 and 5m respectively. Because the flow field near the water-diversion changed drastically, the grid interval at the area was decreased, the cell length was 0.01 m, the remaining area cell grid was 0.02 m, and the total grid number was about 900 000. In the channel model, the inlet boundary of the main channel was set to several volume flow rates, which were 19.96, 25.2, 30.2, 36.5 and 45.32 L/s, respectively; the outlets of the main channel and the side channel were set to be free; the side wall of the channel was selected to have no sliding wall; the air above the free surface was air, and the relative pressure was 0. Based on experiments, FLOW-3D was used to simulate and calculate several flow rate and heights on the rectangular channel water diversion, compared to the measured water depths and velocity. The results showed that the variation of velocity was basically consistent with the measured value and relative error was less than 10%. It was reliable to make numerical analysis on water diversion by using FLOW-3D. The numerical simulation showed that the fluctuation of water surface at the water diversion was affected by the flow rates from the main channel. With the increasing of the bottom height, the maximum velocity and water depth of the side channel inlet section gradually decreased. At the entrance of the side channel, the turbulent kinetic energy near the upstream end was large, while at the downstream end of the branch, the turbulent kinetic energy near the bottom was small. The study provides information on water distribution and water-quantity control in irrigation area.

numerical analysis; flow rate; flow velocity; rectangular channel; bleeder; canal width ratio

王文娥，刘海强，胡笑涛. 侧渠底高对分水口水力特性影响数值模拟研究[J]. 农业工程学报，2019，35(20)：60－68.doi：10.11975/j.issn.1002-6819.2019.20.008 http://www.tcsae.org

Wang Wen’e, Liu Haiqiang, Hu Xiaotao. Numerical simulation of influence of side channel bottom height on hydraulic performance of bleeder[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(20): 60－68. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.20.008 http://www.tcsae.org

2019-02-22

2019-09-10

“十三五”国家重点研发计划（2016YFC0400203）；公益性行业（农业）科研专项（201503125）

王文娥，教授，博士，博士生导师，主要从事流体机械及工程水力学研究。Email：wangwene@nwsuaf.edu.cn

10.11975/j.issn.1002-6819.2019.20.008

S274.4

A

1002-6819(2019)-20-0060-09