LCD改进算法在模拟电路故障诊断中的应用研究
2019-12-18盛沛许爱强张加建李恒李辉
盛沛 许爱强 张加建 李恒 李辉
摘要:提出了一种利用改进LCD算法提取模拟电路故障特征的方法。首先,针对LCD算法估计包络曲线时未考虑其凹凸性的问题,提出了一种改进的LCD算法并尽心了必要的随噪声影响仿真分析;其次,利用该算法对模拟电路被测信号进行分解,得到若干具有物理意义的分量;最后,使用基本尺度熵算法得到故障特征。运用Pearson相关性指标的仿真结果验证了该方法的有效性。
Abstract: A new method of feature vector extraction in analog circuit based on improved LCD algorithm is proposed. Firstly, an improved LCD algorithm is proposed to solve the problem that the convexity of envelope curves is not considered in the standard algorithm. Secondly, the measured signal is decomposed by using thisalgorithm to obtain some signal components of physical significance. Finally, the fault features are obtained by using the basic scale entropy algorithm. The simulation results of Pearson correlation index show the effectiveness of this method.
关键词:信息观点;模拟电路;局部特征尺度分解;基本尺度熵
Key words: information theory view;analog circuit;local feature scale decomposition;basic scale entropy
中图分类号:TN911;E917 文献标识码:A 文章编号:1006-4311(2019)34-0270-03
0 引言
传统的时频分析方法在故障诊断领域取得了众多研究成果,但存在共性问题是缺乏自适应性。进入21世纪以来,在自适应时频分析方法中,研究和应用最广泛的是希尔伯特-黄变换(Hilbert-Huang Transform,HHT)及其改进算法。HHT方法是一种自适应、能适用于非线性、非平稳信号的信号分析方法,由两部分构成:经验模态分解(Empirical Mode Decomposition,EMD)和Hilbert变换[1]。该方法在一定程度上克服了传统时频分析方法的许多不足之处。但EMD、LMD[2]等类似方法在使用过程中存在一些问题:如过/欠包络、端点效应、模态混叠等。因此,国内、外学者寻求EMD的改进、替代方法,开拓了自适应时频分析方法的新思路。湖南大学耿博将EMD算法与神经网络算法相结合,进行了含噪模拟电路的故障识别[3],但缺乏与其它算法的优劣比较;哈尔滨理工大学吕鑫淼将EMD算法与分形维数方法相结合,并借助支持向量机给出了一种设备软故障诊断方法[4],但并未在噪声影响方面做出合理的研究探索。
本文针对上述问题,根据LCD算法的特点,提出一种改进算法,并与标准LCD算法进行比较。更进一步的,利用Person相关性指标验证了该方法的有效性。
1 LCD改进算法
1.1 标准LCD算法[5]
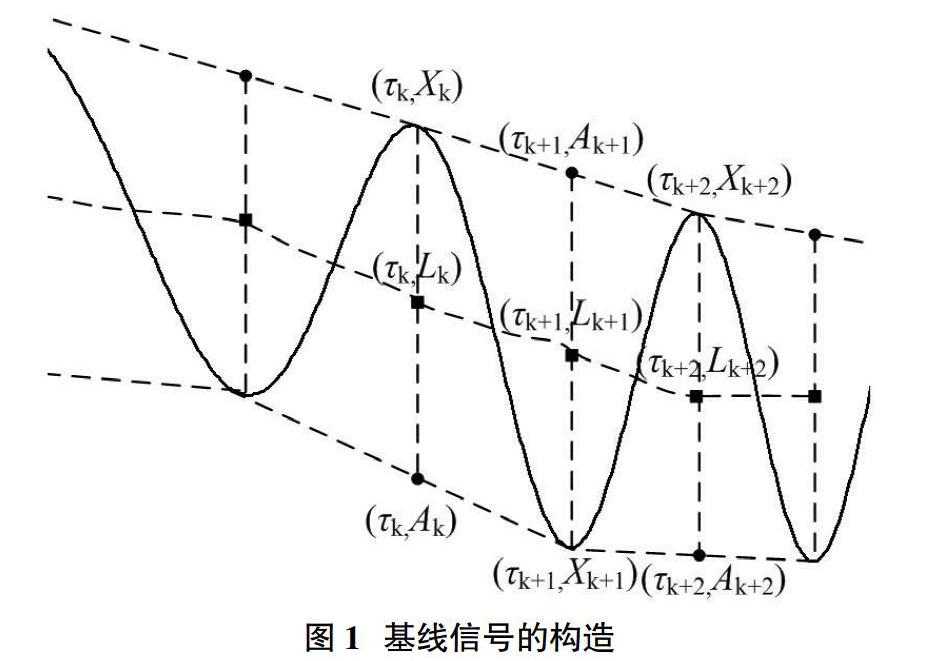
LCD方法的原理是基于单分量信号“局部关于零均值对称”的结论,其基础在于构造均值曲线,并将均值曲线不断从原始信号中分离,直至信号为内禀尺度分量。如图1所示,该方法可概括为:选取相邻极值点并取各线段中点,利用线性变换求得局部均值曲线,将各局部均值曲线相连即得到基线信号,对任意实信号x(t),将均值曲线不断从信号中扣除,就可得到ISC分量,具体过程为可参见文献[5]。
1.2 改进的均值点构造方法
上述标准LCD方法的均值点构造本质上是反复利用三个相邻极值点进行线性差值、反复迭代,包含了3/4波長的信息。该方法的分解质量必然优于包含半波长信息的LMD方法。但是,标准LCD方法采用线性的方法估计包络曲线时,没有考虑曲线段的“上凸”或“下凹”特性,这必然造成了信息的“丢失”。因此,本文在计算某一个极值点对应的均值点时,将该极值点和相邻三个不同类型的极值点作为计算条件,提高均值点的估计精度。
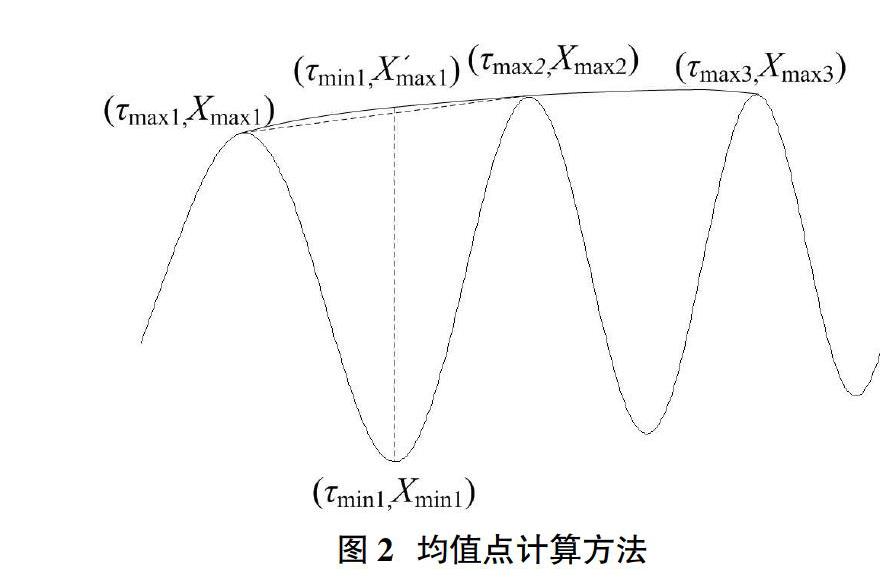
以估计极小值点(τmin1,Xmin1)处的均值点为例,如图2所示,可估计上包络曲线,进而求出上包络曲线在τmin1时刻的值X'max1,对Xmin1、X'max1求均值可得到均值点的估计值。为使上包络曲线足够光滑(在极值点(τmax2,Xmax2)处二阶微分连续),选用三次样条插值(Cubic Spline Interpolation,CSI)方法插值上包络曲线。采用类似的方法可求出下包络曲线,进而得到极大值(τmax2,Xmax2)处的局部均值点。具体的均值点求取流程为:
步骤1:将信号x(t)的极值点Xk及对应的时刻τk进行延拓:
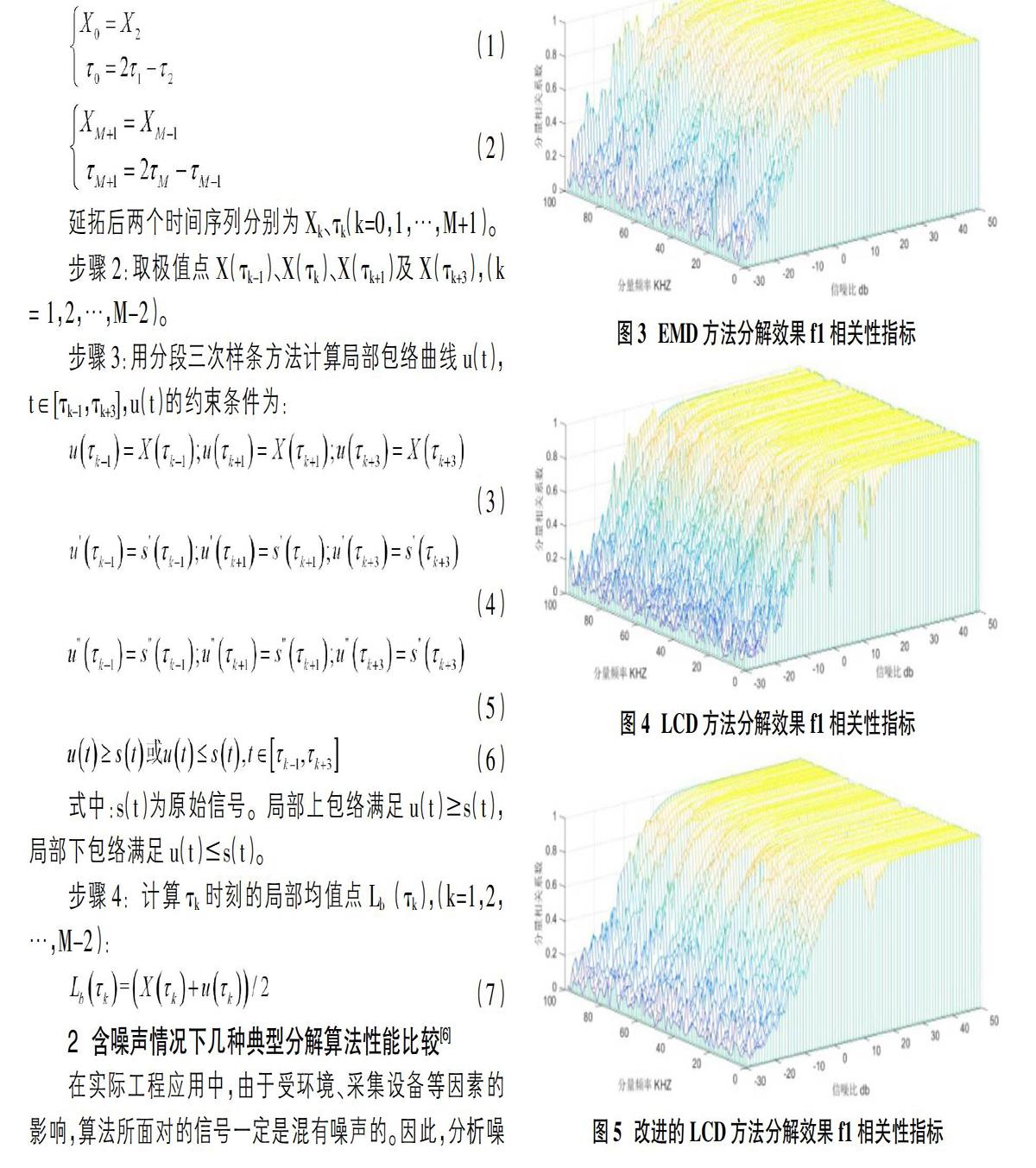
2 含噪声情况下几种典型分解算法性能比较[6]
在实际工程应用中,由于受环境、采集设备等因素的影响,算法所面对的信号一定是混有噪声的。因此,分析噪声对算法的影响显得尤为必要。为了不失一般性,将原始信号频率一并纳入考察范围,考察指标为各算法在加噪情况下所分解得到的各分量与原始信号中相应分量的互相关系数。
具体实现步骤为:
步骤a:设定初始分量频率,初始信噪比SNR,得到初始化的含噪信号;
步骤b:用指定算法对含噪信号进行分解;
步骤c:将各分量信号分别与所有步骤b中所得分量求取互相关系数,并分别取最大值作为最终的互相关系数;
步骤d:增大分量频率f1、f2、f3以及信噪比SNR重复步骤b-c。
按照上述步骤,得到LCD、EMD以及改进的LCD三种算法分解效果随SNR及频率变化图如图所示,这里只给出f1分量相关系数评价指标,其余分量与之类似。可以看出:
①当信噪比大于约20dB以后,各算法分解效果十分理想,先后达到1,其中改进的LCD算法相关性指标更早达到1。
②原始信号频率对各算法分解效果有一定影响,使指标达到1的速度变缓。
③由于步骤a中每次都会对纯净信号重新加入高斯白噪声,因此计算结果会有起伏波动且每次仿真结果都略有出入。这也是为了更好地检查各算法的鲁棒性——显然,EMD鲁棒性较差,改进算法较优。
3 模拟电路仿真实验
选用某型雷达发射机模拟电路中开关电源部分[7]作为验证对象。仿真平台ORCAD CIS和MATLAB16.2。电路图如图6所示,节点OUT为输出测试点。状态集如表1所示。
选取正常状态20组数据(标称值5%容差范围内)、R1↑(超过标称值50%,下同。)故障状态40组数据、C1↓状态40组数据、L1↑状态40组数据,共140组数据。经LCD后的某组典型仿真数据分解结果如图7所示。
分别求出各分量基本尺度熵BE[8]作为故障特征。为进一步验证改进算法有效性,利用PERASON算法求得各分量与原始信号BE互相关系数,如表2所示。
可以看出:
①如图7所示,改进的LCD方法各分量故障特征较为明显,且曲线更加平滑。
②如表1所示,改進的LCD方法较标准方法各分量与原始信号相关性有所提高,证明了该方法的有效性。
③随着分量阶数增加,相关性有下降趋势,可以利用这一点在特征向量选取过程中筛选有用分量,这也正是前文中所述选取前4个分量作为有用分量的原因。
4 结束语
本文针对LCD算法估计包络曲线时未考虑其凹凸性的问题,提出了一种改进的LCD算法并给出了在含噪情况下的分解质量状况。利用互相关系数方法进行的分解性能随噪声影响考察情况表明,改进算法分解性能较优。通过模拟电路仿真实验可以看出,改进LCD算法提取的故障特征较为明显且曲线更加平滑,各分量熵值与原始信号相关性有所提升,并基于此指明了分量的筛选方法。
参考文献:
[1]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995.
[2]Smith J S. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface, 2005, 2(5): 443-454.
[3]耿博,基于EMD算法的模拟电路故障诊断[D].长沙:湖南大学电器与信息工程学院,2014:75-86.
[4]吕鑫淼,基于分形理论的非线性模拟电路软故障诊断方法研究[D].哈尔滨:哈尔滨理工大学,2017:64-75.
[5]程军圣,郑近德,杨宇.一种新的非平稳信号分析方法——局部特征尺度分解法[J].振动工程学报,2012,25(2):215-220.
[6]盛沛,崔伟成.局部特征尺度分解改进算法研究[J].海军航空工程学院学报,2019,32(6):1-5.
[7]王刘军,刘昌锦.基于Hilbert-Huang变换的雷达发射机故障特征提取[J].兵工自动化,2013,32(8):68-70.
[8]李锦,宁新宝.短时心率变异性信号的基本尺度熵分析[J].科学通报,2005,50(14):1438-1441.
