“双8字”型无碳小车循迹原理中的几何关系研究

宋恺殷 金凯乐 李发元

摘要：“双8字”型无碳小车的循迹过程没有电子控制设备的参与，完全由机械结构实现，因此各机构的尺寸、形状、安装位置等几何条件对于轨迹有重要影响。以基于蜗轮蜗杆结构的“双8字”型无碳小车为基础，总结其中对轨迹有重要影响的几何关系，得出数学模型，给出控制“双8字”型无碳小车的轨迹的方法，从而能更加科学地根据要求来调整轨迹。

Abstract： The tracking process of double-8-character carbon-free car is completely realized by mechanical structure without the participation of electronic control equipment， so geometric conditions such as size， shape and installation position of each mechanism have an important impact on the trajectory. The double-8-character type of worm wheel and worm structure is taken as an example to summarize the geometric relationship which has an important impact on the trajectory. The method of controlling the trajectory of the double-8-character type carbon-free car is explored， so that the trajectory can be adjusted more scientifically according to the requirements.

关键词：无碳小车;双8字;循迹;蜗轮蜗杆;轨迹调整;几何关系;数学模型

Key words： carbon-free car;double-8-character;tracking process;worm wheel and worm structure;trajectory adjustment; geometric relations;mathematical model

中图分类号：TP23                                        文献标识码：A                                  文章编号：1006-4311（2019）34-0238-04

0 引言

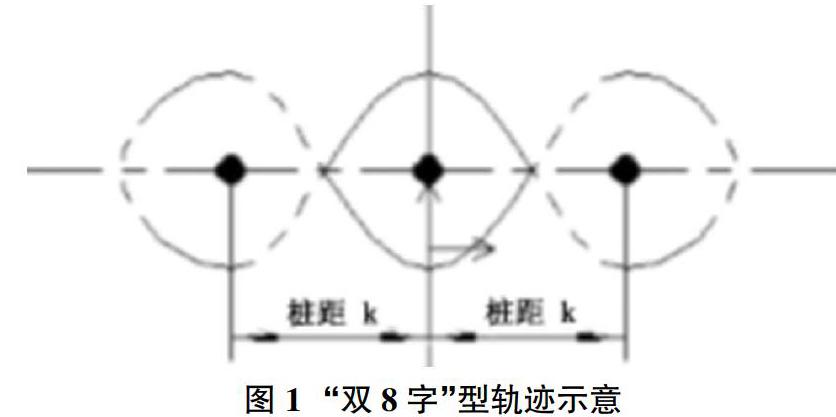
无碳小车是一种仅仅依靠4焦耳（重力加速度g取10m/s2）重力势能作为能量来源的三轮结构小车[1]，旨在实现重力势能的高效利用，节能环保。无碳小车需要实现按照指定路径行进的功能，由于其没有电子控制系统，循迹过程完全由机械结构实现[2]，一些机构的几何特征对于轨迹有关键影响。“双8字”型无碳小车在循迹过程中需要绕桩行进，桩距为变量（350±50mm）轨迹如图1所示。如何根据不同的的桩距来调整小车机械结构中的参数使之能最大限度地完成循迹过程是文中讨论的主要问题。

1  研究背景

目前比较常用的无碳小车的转向微调机构有螺旋测微头机构[3]和蜗轮蜗杆机构[4]。目前的研究主要通过MATLAB进行仿真[5]，能得出理想化的结果。但是无碳小车中的各部分具有耦合关系，各自由度均为不直接可控自由度，并且整车系统中没有反馈使之形成闭环，系统发散。[6]在实际操作过程中，由零件磨损、二次装配精度和场地条件等因素的影响，实际情况可能会与仿真结果有较大的出入，需要进行调整。因此，本文以自主设计的基于蜗轮蜗杆和凸轮机构的“双8字”形无碳小车为研究基础（该构型小车在第六届全国大学生工程能力竞赛中获得了国家级一等奖，证书编号：2019021002）;总结无碳小车在行进过程中的几何关系和几何要素，建立相关数学模型，指导无碳小车的微调过程，使之更好地跑出预期轨迹。研究所用的无碳小车如图2、图3所示。

2  结构方案

2.1 传动机构方案

小车的传动机构如图4所示。重锤绕在定滑轮的小圆上，重锤下落，通过定滑轮转向，从而通过绳子带动凸轮轴旋转。凸轮与大齿轮均与凸轮轴固连，因此凸轮轴转动时大齿轮和凸轮同步转动。大齿轮与小齿轮啮合，大齿轮转动时带动小齿轮转动，小齿轮带动主动轮转动，从而驱动小车前进。从动轮与后轮轴之间安装有轴承，以此来实现差速转向。

2.2 转向机构方案

研究基于自主设计的基于蜗轮蜗杆机构的转向微调机构，使微调过程更清晰直观。利用凸轮机构配合蜗轮蜗杆结果实现转向[7]。转动手拧螺丝将带动蜗杆旋转，从而带动蜗轮旋转。蜗轮和前叉均通过顶丝固连在前轮转向轴上，前轮与前轮轴一起固定在前叉上。蝸轮蜗杆机构具有较高的传动比，能够缩小调节的幅度从而实现更精细的调节。因此可以通过旋转手拧螺丝来实现前轮的初始偏角的微调。

3  几何关系分析

3.1 车定滑轮-凸轮轴传动比与小车最大行进圈数的关系

小车每完成一个“双8”字轨迹的行驶会进行4次变向，即轨迹的曲率中心的所在侧发生四次变化。因此，小车每行驶过一个“双8”字，凸轮必须旋转两圈来完成四次变向。如图4所示，H代表重锤最大的下落距离。则定滑轮旋转的最大圈数凸轮旋转的最大圈数设定滑轮-凸轮轴传动比为P，则于是小车能行驶的最大圈数可以看出，在结构不变和给定重锤下落高度的情况下，定滑轮-凸轮轴的传动比P越大，小车能行驶的圈数越多，且二者成正比关系。

3.2 凸轮安装位置与推杆摆角的关系坐标系和转向机构简化模型如图6所示，凸轮安装位置到前轮转向轴中轴线的Y向距离为d，凸轮轴到前轮转向轴的中心距离为e。由可以求得cosα的值，又角α与β为平行线间对错角，因此cosα=cosβ。又在⊿def中由勾股定理知设推杆的最大x向推进距离为c，则c=b-a。因此在⊿fgc中，依据余弦定理有再对⊿fgc使用一次余弦定理有从而可以求出角θ的值其中a，b，e均为固定量，只有凸轮安装位置到前轮转向轴中轴线的Y向距离d为变量，因此，推杆摆角θ是凸轮安装位置d的单值函数

3.3 轨迹曲率半径与前轮初始偏角和凸轮安装位置的关系 如图7所示建立坐标系。设小车前轮与Y轴的初始夹角为Φ，到达B处时小车前轮与X轴的夹角为ξ，前轮转向轴到后轮轴的中心距离为h（定值），小车行驶到A处时的的曲率半径为i，小车行驶到B处时的曲率半径为j。可以看出而推杆与前轮通过前轮轴固连在一起，因此结合3.2的结论，ξ与Φ具有如下关系于是有即两端的圆弧轨迹的曲率半径仅有前轮的初始偏角决定，而中段圆弧的曲率半径由前轮的初始偏角和凸轮的安装位置共同决定。

3.4 轨迹周长约束关系

小车的前轮轨迹、主动轮轨迹、从动轮轨迹是一组等距曲线。以小车走完一个完整 “双8字”为一周，根据传动关系，每一周凸轮转动两圈，则主动轮转过的圈数设主动轮的轨迹周长为m，结合3.3的分析可知设主动轮的直径为l，轨迹周长应与主动轮行驶距离相等从而有根据张连兆，刘富成，王硕，曹丹丹[8]等人的研究，轨迹的中段圆弧和端段圆弧的曲率半径j和i对于轨迹的形状有影响，轨迹的具体表达式的求解在数学上具有困难，导致Φ和d的关系无法求解。但是通过实验验证得知，在可调范围内，对于给定的d值，仅有唯一的Φ值使轨迹符合要求，即对于给定的d，方程m（？准，d）=c具有唯一解Φ0，因此可以进行函数插值来近似求解d与Φ的关系。

3.5 前轮初始偏角、凸轮安装位置、最适桩距三者间的近似关系

根据3.4的分析，每个d值仅对应一个Φ值使轨迹符合正“双8字”，通过实验可以得到一组映射。

而根据3.3的分析，每一组（di，Φi）都对应一个不同的轨迹，即每一组（di，Φi）对应一个最合适的桩距ki，于是得到映射。

利用拉格朗日插值多项式进行函数插值[9]由此即可以建立Φ关于d的插值多项式Φn（d）和k关于d的插值多项式kn（d）。其插值余项

4  实际测试

以西北工业大学无碳小车创新实践基地中基础基本相同两组成员为实验样本，两组成员使用相同“双8字”型无碳小车，该小车与本研究所基于的无碳小车构型相同。告知其中一组成员上述内容并指导其结合实际数据进行计算与调整，另一组给予相同的时间条件，但不提供理论指导。实验结果以行进的最大圈数为指标，每完成一个“双8”字轨迹的行驶记为完成一圈，圈数越多代表成绩越好。每组测试三次，测试结果见表1。

组2在测试中重锤均未能下落到最底端，在重锤下落完全之前小车便撞桩停止行进，造成了重力势能的大量浪费。而组1则在被告知和指导使用本分析后跑出了42圈的成绩，重锤下落至最底端。可见，本分析对于无碳小车轨迹调整的指导意义显著。

5  结束语

本研究对“双8字”型无碳小车进行了一系列的几何关系分析，揭示了“双8字”型小车的循迹原理，着重分析了凸轮安装位置和前轮初始偏角对轨迹的影响，利用函数插值的方法进行拟合，指出了如何调整凸轮的初始位置和前轮的初始偏角使轨迹与给定的障碍桩距相适应的方法。经过实验验证，该方法对于无碳小车的轨迹调整的指导作用显著，使之能够有效地利用重力势能。

参考文献：

[1]胡越铭，高德文，张瑞，张欣，高轩. 基于凸轮组合机构的“8”字形无碳小车创新设计[J].北方工业大学学报，2014，26（01）：38-43.

[2]武时会.双“8”字形无炭小车纯机械设计[J].科技风，2018（34）：7-8.

[3]兰京.“S”型无碳小车创新设计[J].内燃机与配件，2019（08）：207-209.

[4]吴亚坤，王会良，李晨曦，于海洋，李凯乐.双“8”字绕障无碳小车的创新设计[J].科学技术与创新，2019（10）：154-155.

[5]季元进，任利惠，顾建.利用变心齿轮传动的无碳小车的机构创新设计[J].机械设计，2014，31（03）：71-74.

[6]陈晓航，刘德锋，左传，徐敏.基于ADAMS的空间RSSR机构轨迹仿真探究[J].机械研究与应用，2017，30（01）：69-71.

[7]KOTAKE Shigeo. 508 General Cam Curve Decided from Discrete Aimed Trajectory of Output Mass in Cam-Follower Oscillator and Aimed Dwell Conditions[J]. The Proceedings of Conference of Kansai Branch，2015（90）：173-176.

[8]張连兆，刘富成，王硕，曹丹丹.基于凸轮的“双8”字无碳小车设计[J].南方农机，2019，50（09）：131-132，148.

[9]聂玉峰，王振海.数值方法简明教程[M].北京：高等教育出版社，2011：60-64.