Electron-impact ionization cross section calculations for lithium-like ions

Guo-Jie Bian(卞国杰) Jyh-Ching Chang(张稚卿) Ke-Ning Huang(黄克宁) Chen-Sheng Wu(武晨晟)Yong-Jun Cheng(程勇军) Kai Wang(王凯) and Yong Wu(吴勇)

1National Key Laboratory of Computational Physics,Institute of Applied Physics and Computational Mathematics,Beijing 100088,China

2Department of Physics,National Tsing Hua University,Hsinchu 300,China

3Institute of Atomic and Molecular Physics,Sichuan University,Chengdu 610065,China

4School of Physics and Information Technology,Shaanxi Normal University,Xi’an 710119,China

5Hebei Key Laboratory of Optic-electronic Information and Materials,The College of Physics Science and Technology,Hebei University,Baoding 071002,China

6HEDPS,Center for Applied Physics and Technology,and College of Engineering,Peking University,Beijing 100871,China

Keywords: total cross sections,electron-impact ionization,excitation-autoionization,distorted-wave

1. Introduction

Electron-impact ionization is an important physical process in plasma environment. Nonequilibrium plasma simulations, such as magnetic confinement fusion, inertial confinement fusion, and astrophysics, require a large amount of data on cross sections of electron-impact ionization,in which ionization cross sections directly affect the charge transfer and energy transport of the plasma state.[1-6]A great deal of attention has been paid to the electron-impact ionization for lithium isoelectronic sequence due to the K-L excitationautoionization process, which plays an important role in ionization dynamics.[7,8]Although much work has been devoted to improving the theory of electron-impact ionization, there are still discrepancies between theoretical predictions and experimental data for some members of the sequence.[9,10]Therefore, it is of vital importance to investigate behavior of electron-impact ionization along the isoelectronic sequence.

Experimentally, the modulated crossed-beam technique is commonly used in measurements of electron-impact ionization. Lithium isoelectronic sequence has been extensively investigated in lowZions. Absolute cross sections have been measured for Be+, B2+, C3+, N4+, O5+, and Ne7+ions[7,11-17]in the energy range of 18-2000 eV.Wonget al.[18]measured cross sections for Ti19+, V20+, Cr21+, Mn22+, and Fe23+ions at approximately 2.3 times ionization energy with typical uncertainties of 10%. Moreover, Ba53+ion was measured at 22 keV,[19]and U89+ion was also be measured.[20]

Theoretically, extensive calculations have been performed with various methods.The most commonly used method for direct ionization is the Coulomb-Born approximation,[21]in which the continuum electrons are regarded as Coulomb or distorted waves. Younger[22,23]introduced several applications of the Coulomb-Born and distorted-wave approximations, which produced results for hydrogen-, helium- and lithium-like ions. However, performance of the Coulomb-Born method is poor and, in many cases, it overestimates total cross sections. The electron exchange in transition matrix elements and Coulomb distortion waves are observed to be vital.Jakubowicz and Moores[9]discussed the Coulomb-Born exchange and distorted-wave exchange approximations, which solved the problems in the inclusion of exchange for the positive ions. When the indirect process is dominant, the close-coupling method is considered to be an effective prescription to describe the quasibound states of the target ion.[9]Fursa and Bray[24]presented the electron-helium scattering with convergent close-coupling formulations. This method requires numerous computations and applies only to a system with few valence electrons. The initial and final states of electron-impact ionization process for neutral helium were studied in the R-matrix basis,[25]which is a combined distorted-wave and close-coupling approach. A special feature of this method is the consistency of the initial bound state and the final continuum state of the ions. Furthermore, the R-matrix method, which is independent of the energy of the scattered electrons in the inner region, was extended to the electron-impact ionization of Ne7+.[10]

In recent years,the two-potential distorted-wave(TPDW)approximation, which uses different asymptotic charges for the distorting potential to study the mutual screening of the faster and slower electrons, has been developed and widely used in the calculation of electron-, positron-, and protonimpact ionizations of hydrogen-, helium-, and beryllium-like ions.[26-34]Compared with other theoretical and experimental data, generally more reliable results are obtained in these works.

2. Theory

whereJ0is the total angular momentum of the target,andTfiis the appropriate transition amplitude. The real amplitudedαis defined by the reduced matrix element of the partial-wave amplitude in channelα,

whereσκpandσκsare the Coulomb phase shifts of the two outing electrons,the index i refers to the incident electron,JαandJare the total angular momentum of the residual ion and of the entire collision complex,andHIis the appropriate interaction Hamiltonian.

The direct-ionization cross sections can be calculated as

Here,αiandβiare the Dirac 4×4 matrices,andpirepresents the momentum operator. Before the collision,subscript 1 represents the incident electron,andi=2,3,4 are the indices for bounded electrons. According to two-potential distorted-wave formulation,the potentialViis separated into the distorting potentialUiand the residual potentialWi. They are defined as

The distorting potentials can be approximated as Coulomb potential from the nuclei and the average screened potential,corresponding to the asymptotic chargesZpandZs.In this work, three models of distorting potential are applied in the calculation, and some information of these potentials is listed in Table 1. Models TPDW00 and TPDW11 are two extreme models for the electron-impact ionization process.In model TPDW00, the scattered electrons are completely screened from each other,so they experience the same distorting potential as the incident electron. In model TPDW11,it is completely free from the mutual screening effects by scattered electrons, thus both outgoing electrons are only affected by the bound electrons and the nucleus. The model TPDW01 is closer to the real scene,where the faster electron is completely screened by the slower electron in the asymptotic region, so that the faster electron is affected by the asymptotic charge ofZ-3, and the slower electron is affected by the asymptotic charge ofZ-2. The average screened potential due to the residual electrons of helium-like ions inUpandUsis given by

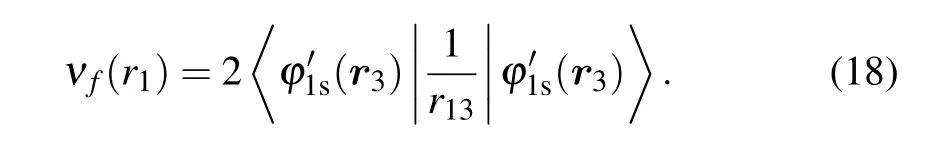
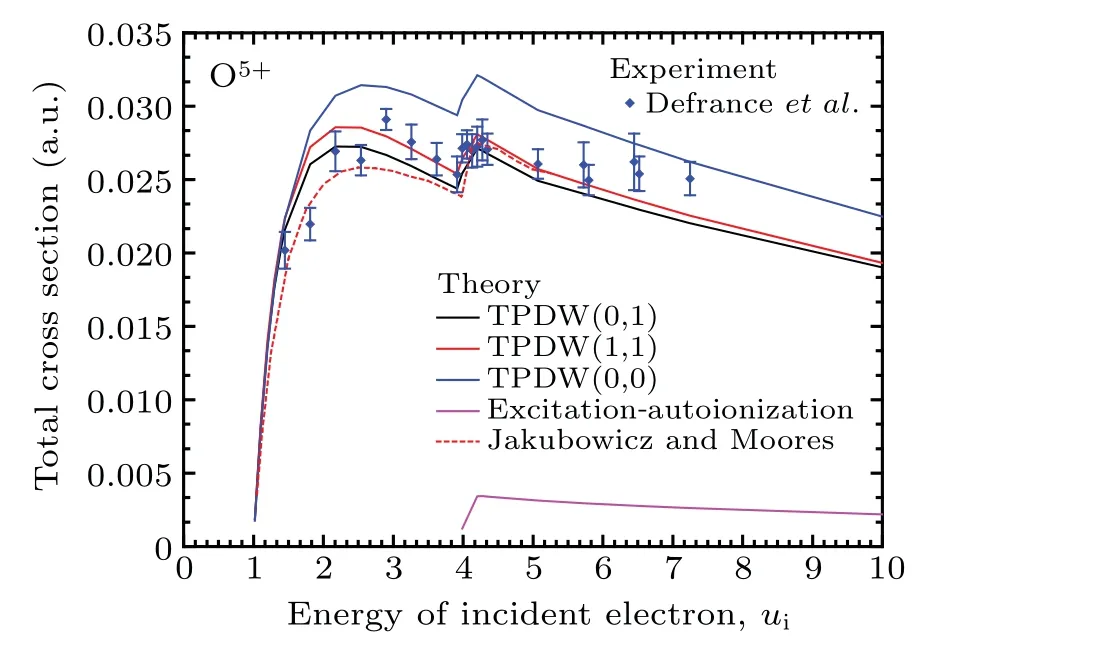
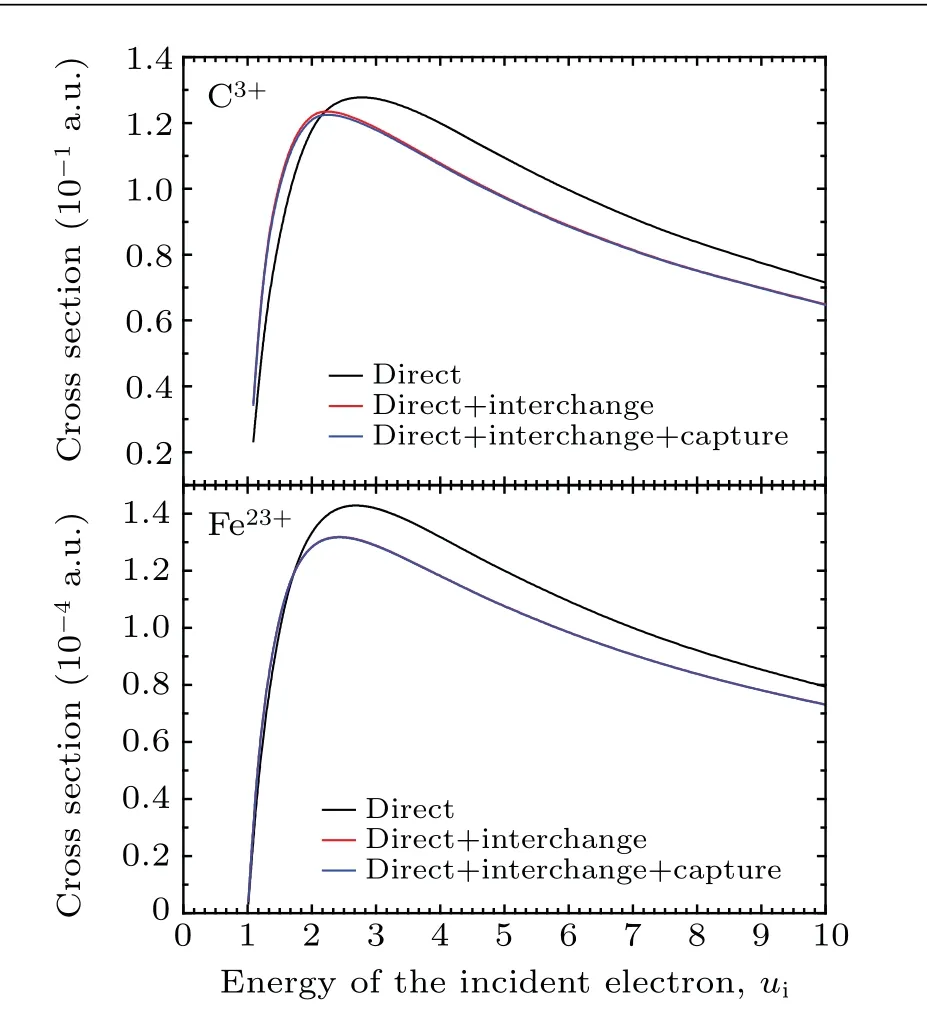
Considering the important contributions from the indirect ionization process, we calculate the cross sections of indirect ionization using the R-matix method,[37]in which the configuration space is divided into two regions at a spherical radiusr=a. For the boundary ofr

where the(N+1)-electron exchange effects are important and must be taken into account. For the boundary ofr>a, the amplitude of the bound wave function is negligible, and then the exchange interaction between the bound and the continuous electrons can be ignored. For electron-impact ionization of lithium-like ions,the K-L excitation-autoionization process will cause a rapid enhancement of the cross sections at about four times the ionization energy. In present work,the intermediate states 1s2l2l′formed by the 1s electron excited ton=2 orbitals are included and partial wave contributions up to angular momentumL=7 are included to obtain converged ionization cross sections,in which the 1s2l2l′2Se,2Poresonances dominate the excitation-autoionization contributions.[9,10]

The indirect-ionization cross sections is calculated as

转弯速度：当铁丝直径为8 毫米时，转弯速度为5000 时能完成循迹转弯，但速度过慢，加速到5600 时能完成循迹且时间最短，当加速到6000 时小车速度过快易冲出赛道。

2.1. Total cross sections

In the present work, we have calculated the total cross sections of electron-impact ionization for C3+, N4+, O5+,Ne7+and Fe23+ions with incident energiesuiin the range of threshold energy units from 1 to 10. The two-potential distorted-wave method is used in the lower energy region,and when the incident energy is above the autoionization threshold, the distorted-wave combined with the R-matrix method is employed to calculate the contributions from the excitation-autoionization process. The bound-state wavefunctions and ionization energies of Li-like ions are generated from a multi-configuration Dirac-Fock (MCDF) calculation,which is implemented in the relativistic MCDF code written by Desclaux.[39]

One distinct feature of the ionization cross section for lithium-like ions is the important role played by the excitationautoionization mechanism at the energies between three and five times the direct ionization threshold,which is completely different from the cases of beryllium and boron sequences.For example,this effect contributes approximately 17%of the total ionization cross section of Ne7+, while it is smaller in Ne6+and not observed for Ne5+.[7]In addition,the contribution from the excitation-autoionization process is dominated by 1s2l2l′intermediate states. Therefore, the configurations of 1s2s2, 1s2s2p and 1s2p2are included, where the configurations of 1s2s22Seand 1s2s2p2Podominate the excitationautoionization contributions; the other resonances have minimal contributions to the cross sections.[9,10]The energies and total cross sections are given at autoionization resonance hump in Table 2, along with the other theoretical results and experimental data. Our calculations are close to the experiments and the Coulomb-Born exchange approximation with closecoupling results.[9]Generally,the model TPDW11 is in good agreement with the experimental measurements for the largest difference less than 5%. The only exception is for Ne7+ion,

where the TPDW00 model behaves well and there is a 10%discrepancy between TPDW00 and TPDW11 models.

Table 2. Energies E (eV)and total cross sections σ (10-3 a.u.)at the positions of autoionization resonances for lithium-like ions.

The total cross sections produced by using the models TPDW00, TPDW01 and TPDW11 for the ions C3+, N4+,O5+, Ne7+and Fe23+are presented in Figs. 1-5, along with available experimental data and theoretical results. Generally the ionization cross section is a slow and smooth varying function of the incident electron energy, but sharp peak appears at about four times the ionization energy. The cross sections using three models appear to be very similar with each other at the low energies, so we present the results in Table 3. The results generated by the TPDW00 model are smaller than TPDW01 and TPDW11 at less than 1.25 times the ionization energy and are larger in higher incident energy. At small incident energies, the model TPDW00 accurately describes continuous electrons because two electrons are screened each other by sharing a small kinetic energy. At large incident energies,the model TPDW01 or TPDW11 is expected to be more reliable,since at least one scattered electron possesses a large kinetic energy,which generates small screening effects. The results of three models become similar as the nuclear chargeZincreases because the nuclear potential dominates the cross section of highly charged ions such that the mutual screening effects of continuous electrons affect negligibly. We also present the excitation-autoionization contributions for C3+, N4+, O5+, Ne7+and Fe23+ions from Figs.1-5.Obviously,the excitation-autoionization mechanism plays a significant role for all the ions. The contributions are approximately 15%of the total cross section at formant in C3+,N4+,O5+, and Ne7+ions, while it is less than 7% for Fe23+ion.Another interesting feature is the shift of the resonant peak toward the lower energy with an increase in the number of nuclear charges. The peak position is about five times the ionization energy for C3+ion,but drops to about three times the ionization energy for Fe23+ion. Note that the cross sections caused by the direct inner-shell ionization are also considered when the incident electron energy is greater than the 1sionization energy threshold, and this contribution never exceeds 15%.

Table 3. The total cross sections σ (10-3 a.u.) are calculated for lithium-like ions near the threshold with the models TPDW00,TPDW01 and TPDW11,respectively.

Figure 1 shows the total cross sections for C3+, along with the theoretical values[9]and the experimental results[15]with their uncertainty of about 12%. The agreement between the Coulomb-Born exchange results and experiment is good below 2.5 times the ionization energy. After that, the discrepancy has become more pronounced. As is expected, the TPDW00 model results are much higher than experiment except near the threshold. The TPDW01 or TPDW11 model appears to be somewhat larger compared with the measurements before the peak of direct ionization, with a difference less than 6%. The TPDW11 model is in better agreement with experiment in the autoionization region than Coulomb-Born exchange. Figures 2 and 3 depict the two-potential data for N4+and O5+together with the experimental results,[17]and the theoretical values with the Coulomb-Born exchange method,[9]respectively. Here, the theoretical results containing the excitation-autoionization contributions are discussed.Similarly, the TPDW00 model is higher than experiment,while,this difference becomes smaller with the nuclear charge increasing. The Coulomb-Born exchange approximation is again smaller than our results of two-potential distorted-wave in direct process. However, since the distortion effects will be small at the high energies of autoionization region, the coulomb-wave and distorted-wave results tend to be close.For both ions,the TPDW11 results are in excellent agreement with the experiments.

Fig. 1. Electron-impact ionization cross sections of C3+ (ionization energy = 64.385 eV). The solid curves represent the two-potential distorted-wave calculations with models TPDW00, TPDW01, and TPDW11 and the results of excitation-autoionization. The Coulomb-Born exchange results[9] with dashed curve and the experimental data[15] with solid dot are shown for comparison.

Figure 4 shows the theoretical results of Ne7+,which include the excitation-autoionization contribution using closecoupling approximation[9]and with the distorted waves-Rmatrix method.[10]The Coulomb-Born exchange calculation underestimates the direct ionization contribution below the autoionization threshold, whereas the excitation-autoionization contribution is consistent with the present results. Moreover,the direct ionization cross sections of Riahiet al.[10]are lower than others and the excitation-autoionization contributions seem to be overestimated using the R-matrix method.With the nuclear charge increasing, the TPDW00 model is found to be closer to the measurements.[7,17]Our two-potential results provide an excellent estimation for incident energies in the ranging of threshold energy units from 1 to 10.

Fig. 2. Electron-impact ionization cross sections of N4+ (ionization energy = 97.777 eV). The solid curves represent the two-potential distorted-wave calculations with models TPDW00, TPDW01, and TPDW11 and the results of excitation-autoionization. The Coulomb-Born exchange results[9] with dashed curve and the experimental data[17] with solid dots are shown for comparison.

Fig. 3. Electron-impact ionization cross sections of O5+ (ionization energy = 138.006 eV). The solid curves represent the two-potential distorted-wave calculations with models TPDW00, TPDW01, and TPDW11 and the results of excitation-autoionization. The Coulomb-Born exchange results[9] with dashed curve and the experimental data[17] with solid dots are shown for comparison.

Fig. 4. Electron-impact ionization cross sections of Ne7+ (ionization energy = 238.996 eV). The solid curves represent the two-potential distorted-wave calculations with models TPDW00, TPDW01, and TPDW11 and the results of excitation-autoionization. The Coulomb-Born exchange results[9] with dashed curve, the distorted waves-Rmatrix results[10]with dotted curve,and the experimental data[7,17]with solid dots are shown for comparison.

Figure 5 shows our data of Fe23+ion, as well as theoretical data[9]and the experiment.[18]Our results are slightly higher than those of Coulomb-Born exchange approximation,in which the relativistic effect is not included. However, the relativistic corrections are important for the case of Fe23+ion.The effect of distortion decreases with increasing charge as expected,and all calculations are more or less consistent.

Fig. 5. Electron-impact ionization cross sections of Fe23+ (ionization energy =2046.634 eV). The solid curves represent the two-potential distorted-wave calculations with models TPDW00, TPDW01, and TPDW11 and the results of excitation-autoionization. The Coulomb-Born exchange results[9] with dashed curve and the experimental data[18] with solid dots are shown for comparison.

2.2. Contributions from exchange effect

Since the transition matrix element has been separated into direct,interchange,and capture parts in Eq.(10),we can explore the contributions from different terms in the potential,which is also of great interest in the studies of ionization dynamics. As an example, a separation of the contributions on the total cross sections of C3+and Fe23+ions from model TPDW01 are presented in Fig. 6. Obviously, the direct part plays a major role in both ions. The interchange terms increase the cross sections by 50% near the threshold and decrease them by about 10% after the peak. For C3+ion, the contributions from capture terms are negative and influence on the cross sections is less than 2%. For Fe23+,the trend of the capture terms is similar to the low-Zions, but the proportion decreases to 0.2%.

It is observed that the capture terms have more contribution for lower-Zions, but become negligible for higher-Zions in the selected targets. The bound electrons of lower-Zions spread wider, so that there is more opportunity for incident electron to overlap and exchange energy with bound electrons. Simultaneously, because the incident electron spends more time to interact with target near the threshold, the exchange effects become more significant. Moreover, the radial integral〈WpbRλWsi〉in the interchange terms[40]become larger;thus the interchange terms contribute significantly near the threshold. However, the bound electrons are more tightly bound together, so there are fewer opportunities to exchange with the incident electron for higher-Zions.

Fig. 6. Contributions from exchange effects on the cross sections of C3+ and Fe23+ in the model TPDW01.

3. Conclusion

We have applied the two-potential distorted-wave and Rmatrix methods to describe the electron-impact ionization with direct and indirect mechanisms for selected lithium-like ions.Several sets of asymptotic charges in three models TPDW00,TPDW01 and TPDW11 are used to characterize the effects of mutual screening from scattered electrons.The total cross sections obtained in the present work for the lithium isoelectronic sequence show good agreement with experimental results. It is found that the model TPDW00 better describes the electronimpact ionization process at lower incident energies,whereas the model TPDW01/TPDW11 works better at higher incident energies. With the nuclear charge increasing, the TPDW00 model becomes more reliable. The contributions from the exchange amplitudes, including the interchange and capture parts,are also discussed in the present work. The interchange term is important for all the isoelectronic sequence and the contribution of capture term only becomes non-negligible for the case of lower-Z ions. Furthermore, the K-L excitationautoionization processes are non-negligible for lithium-like ions, which contribute at most 7%-15% in the present total cross section calculations.This work can provide a set of highprecision ionization cross section data for related plasma simulations,and it can also provide a reference for future studies with more sophisticated methods.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant Nos. 11934004 and U1832201),the Science Challenge Project (Grant No. TZ2016005), and the CAEP Foundation(Grant No.CX2019022).