概率中的错误类型剖析
2019-12-17李燕华
李燕华


概率属于初中数学中“统计与概率”的知识范畴,是描述一类事件发生的可能性大小的数学模型。它是中考必考的知识点,重点考查大家数据剖析与数学建模的素养。在学习过程中,许多同学对概率知识的理解不准确,往往会出现各种错误,下面结合几种常见的错误类型进行归类剖析,希望对同学们今后的学习有所帮助与启迪。
一、频率与概率混淆不清易出错
例1 小明抛掷一枚硬币20次,有13次正面朝上,当他抛第21次时,正面朝上的概率是。
【错解】[1320]。
【剖析】错误的原因是没有真正理解概率的本质,把概率与频率混为一谈。概率与频率是两个不同的概念,概率是事件的本质属性,其取值不依赖于试验的次数。当然两者又具有密切的关系:当重复试验次数足够多时,频率会稳定在概率附近,所以概率的大小可以通过数次试验得到的稳定频率去估计,但要注意频率并不等同于概率。况且本例中试验的次数太少,所以不能把频率作为概率的估计值。
抛掷一枚硬币时,因为每次试验都有2种等可能的结果,而抛到正面朝上的只有1种,所以第21次时与前面每次情况一样,正面朝上的概率都是[12]。
【正解】[12]。
二、概率计算公式不清易出错
例2 相同方向行驶的两辆汽车经过同一个“T”字路口时,可能向左转或向右转。如果这两种可能性大小相同,则这两辆汽车经过该路口时,都向右转的概率是()。
A.[14] B.[13] C.[23] D.[12]
【错解】D。
【剖析】有些同学错误地认为,经过同一个“T”字路口时,选择一条路有向左转、向右转两种结果,概率都是[12],出现这种错误想法的根本原因是对等可能条件下概率的计算方法模糊不清,没有考虑到所有等可能的结果数。
在等可能条件下概率的计算公式为:P(A)=[mn],其中n表示所有等可能出现的结果数,m表示事件A发生可能出现的结果数。解决本题,不仅要正确理解、掌握公式,还要能熟练地利用列表法或画树状图法确定公式中的m、n的值。
【正解】A。
画树状图剖析如下:
∵共有4种等可能的结果数,都向右转的只有1种结果,
∴P(都向右转)=[14]。
三、试验次数分辨不清易出错
例3 甲、乙、丙三位同学在操场上互相传球,假设他们相互间传球是等可能的,并且由甲首先开始传球。
(1)经过2次传球后,球仍回到甲手中的概率是;
(2)请用列举法(画树状图或列表)求经过3次传球后,球仍回到甲手中的概率。
【错解】(1)[13]。
画树状图如下:
∵共有6種等可能的结果数,经过2次传球后,球仍回到甲手中的有2种结果,∴P(球仍回到甲手中)=[13]。
(2)画树状图如下:
∵共有4种等可能的结果数,经过三次传球,球仍回到甲手中的有2种结果,∴P(球仍回到甲手中)=[24]=[12]。
【剖析】(1)本题求解错误的同学不理解“甲首先开始传球”的意义,想当然地以为开始就传给甲、乙、丙三人。如果我们可以设身处地地想一下,甲首先传球的结果中是不可能再传给自己的。
(2)有的同学不理解“三次传球”的结果的意义,以为“甲首先开始传球”就是一次了,其实这只是“甲开始传球”,不是第一次传出球的结果,这样就不能正确画出树状图。
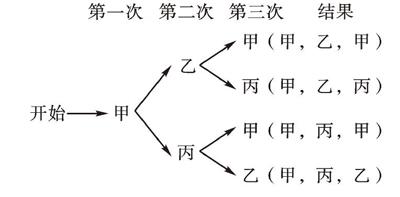
【正解】(1)画树状图为:
∵共有4种等可能的结果数,经过2次传球后,球仍回到甲手中的有2种结果,∴P(球仍回到甲手中)=[24]=[12]。
(2)画树状图为:
∵共有8种等可能的结果数,经过三次传球,球仍回到甲手中的有2种结果,∴P(球仍回到甲手中)=[28]=[14]。
答:经过三次传球后球仍回到甲手里的概率是[14]。
四、是否放回未分辨易出错
例4 三张外观相同的卡片分别标有数字1、2、3,从中随机一次抽出两张,这两张卡片上的数字恰好都小于3的概率是。
【错解】[49]。
画树状图得:
∵共有9种等可能的结果,而两张卡片上的数字恰好都小于3的有4种结果,
∴P(两张卡片上的数字恰好都小于3)=[49]。
【剖析】导致本题求解错误的原因是审题不清,忽略了问题中的一个重要条件“从中随机一次抽出两张”,有些同学不能很好地理解其含义,其类似于“从中随机抽出一张不放回,再从剩下的抽出一张”,故在此条件下进行试验,最后结果中不可能出现抽出的两张卡片上的数字完全相同的情况。
【正解】画树状图得:
∵共有6种等可能的结果,而两张卡片上的数字恰好都小于3的有2种结果,
∴P(两张卡片上的数字恰好都小于3)=[26]=[13]。
五、实际应用理解不当易出错
例5 汤姆斯杯世界男子羽毛球团体赛小组赛比赛规则:两队之间进行五局比赛,其中三局单打,两局双打,五局比赛必须全部打完,赢得三局及以上的队获胜。假如甲,乙两队每局获胜的机会相同。现甲队在前两局比赛中已取得2∶0的领先,那么甲队最终获胜的概率是多少?
【错解】画树状图为:
∵共有4种等可能的结果数,其中甲至少胜一局的有3种结果,
∴P(甲队最终获胜)=[34]。
【剖析】部分同学不理解此题中“五局比赛必须全部打完”“甲队在前两局比赛中已取得2:0的领先”的意义。有的同学认为再打两局,甲队胜一局就胜,有的同学认为再打三局,甲队要全胜才最终胜,有的同学认为要求5次的概率,太麻烦了……没有真正理解在那样的条件下,再打三局,只要找出甲至少胜一局的结果数,然后根据概率公式求解。
【正解】画树状图为:
∵共有8种等可能的结果数,其中甲至少胜一局的有7种结果,
∴P(甲队最终获胜)=[78]。
(作者单位:江苏省常州市新北区小河中学)
