基于小波阈值和约束独立分量分析的齿轮故障诊断研究

韩博跃， 郝如江， 安雪君

（石家庄铁道大学 机械工程学院，河北 石家庄 050043）

随着科学技术的发展，机械设备结构越来越复杂，组成部件越来越多，作为传递运动和动力的齿轮几乎在任何大型机械设备中都有着极其重要的作用，齿轮的健康状态对于设备的安全运行至关重要。因此，对齿轮进行故障诊断具有重要意义［1］。

独立分量分析（ICA）是一种从混合信号中分离出具有独立统计特性的单个源信号的分离方法。由于其在分离过程中需要的独立源信号的先验信息很少，并且有明显的分离效果，ICA 已在无线通信、语音处理和机械故障诊断等领域具有广泛的应用［2-4］。在实际应用中，因为源信号次序不确定性和数目不容易确定等问题，限制了其在齿轮故障特征提取中的应用。近年来，在ICA 基础上发展起来的约束独立分量分析（CICA）对其算法进行改进，将上述问题有效地解决［5-7］，它在不需要知道源信号数量情况下，首先利用先验信息产生参考信号，进而提取出感兴趣的独立分量。CICA 算法在解决无噪声或者低噪声多元信息混叠时，分离效果非常明显，当在强噪声环境下，分离效果不太理想。

齿轮的振动信号常常是叠加有强噪声的，小波变换具有良好的时频局部化和多分辨率分析的特点，因而适用于非平稳信号和强噪声信号的处理，具备良好的降噪能力。为了成功提取出齿轮的故障特征，本文提出了基于小波阈值和CICA 相结合的算法，并对该算法进行了仿真信号和实验测试信号的分析，结果显示，该算法具有很好故障特征的分离效果。

1 小波阈值降噪原理

在实际工程中，有用信号通常为低频信号或是一些比较平稳的信号，而噪声信号则通常表现为高频信号。因此预处理降噪过程可以按如下方法进行处理：首先用小波算法对信号进行分解，以门限阈值等形式对小波系数进行处理；然后再对分解的信号进行重构，达到降噪的效果。

小波降噪的方法主要有基于模极大值降噪法、平移不变量降噪法和小波阈值降噪法。本文选择小波阈值降噪方法进行预处理降噪，小波阈值法降噪的基本步骤如下［8-9］：①小波基函数的选择。小波基函数的正则性及波形与数据的结构相似程度会影响信号降噪的效果，sym N 小波基与机械振动波形相似，其中，sym8小波因为具有良好的对称性和连续性，并且具有紧支集，因此选择sym8小波。②分解层数的确定。不同分解层数降噪效果不同，要合理选择分解层数，文中选择三层分解。③阈值和阈值函数的选取。阈值估计方法主要有：无偏似然估计原则、极值阈值原则、分层可变阈值、heursure规则和固定阈值原则等［8-9］。阈值函数主要分为软阈值函数和硬阈值函数。经过硬阈值函数处理的信号，降噪后信号的部分特征可以得到很好的保留，但是用它降噪经常会产生比较大的方差；而经过软阈值函数处理的信号降噪效果平滑，并且不会出现附加震荡［10-12］。本文根据固定阈值原则选用软阈值函数进行降噪。④进行小波重构，得到降噪处理后的信号。

2 约束独立分量分析（CICA）

2.1 ICA模型

N 维混合观测信号X＝［X1，X2，…，XN］T与M 维独立源信号S＝［S1，S2，…，SN］T的ICA 模型为

式中，A 为N×M 维混合矩阵；N、M 分别为正整数。

ICA 算法是在不知道源信号S 和混合矩阵A 的条件下确定分离矩阵W，使得到的独立分量向量y 最佳接近源信号S，其分离表达式为

在判定分离分量独立性上，主要有基于峭度极判据和基于负熵极大判据［13-14］。选择基于负熵极大判据，其表达式如下

式中，J（y）为向量y的负熵；H（ygauss）、H（y）分别为向量ygauss、向量y 的熵；ygauss为一个高斯向量，具有相同的协方差。

根据定义计算向量的负熵，必须要知道概率密度函数，但是在实际应用中很难获知独立成分的概率密度函数，所以只能采用近似方法来求解负熵，即

式中，ρ为正常数；μ 为白化型高斯变量；E｛·｝为期望值；G（·）为非线性函数。

2.2 CICA模型

CICA 算法建立在ICA 算法基础上，基于源信号的先验知识生成参考信号，从而提取出与参考信号最相似的一个独立分量［14］。基于源信号已知信息构造参考脉冲信号r（t），将待提取的目标信号y 和参考信号r（t）的距离函数定义为ε（y，r），用来表示目标信号与参考信号的接近程度。ε（y，r）可用均方误差ε（y，r）＝E｛（y-r）｝度量，CICA 算法的数学模型如式（5）和式（6）所示。

目标函数

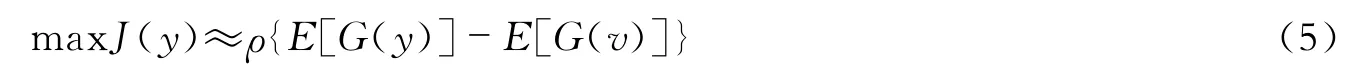
约束条件

式中，ρ为正常数；G（·）为非线性函数；v为具有与y 相同协方差矩阵的高斯变量；ξ为阈值。式（6）实际上是一个约束优化问题，通过拉格朗日乘数法对其求解，可得到源信号的最佳估计，提取出目标源信号。

参考信号的选取条件如下：①参考信号要含有期望信号的一些先验信息，但是无须与期望信号一样；②参考信号需要具有非高斯性，这样才能使算法收敛于期望信号。机械设备在工况稳定的情况下，齿轮的故障信号表现为固定频率的脉冲序列，齿轮的故障特征频率就可以作为约束独立分量分析的约束条件［15］，建立基于脉冲的参考信号，即构建一个周期脉冲信号作为CICA 算法中的参考信号，周期脉冲信号的频率与齿轮故障特征频率一致。

3 基于小波阈值和CICA的齿轮故障诊断

小波阈值和CICA 相结合用于齿轮箱故障信号的分析，流程如图1所示。因为CICA 算法对信号中叠加的加性噪声十分敏感，为了提高CICA 算法的稳定性和分离效果，对其加入小波软阈值降噪进行预处理来提高信噪比，再进行信号的分离。

4 仿真分析

为了验证方法的有效性，进行仿真信号分析。源信号表达式为

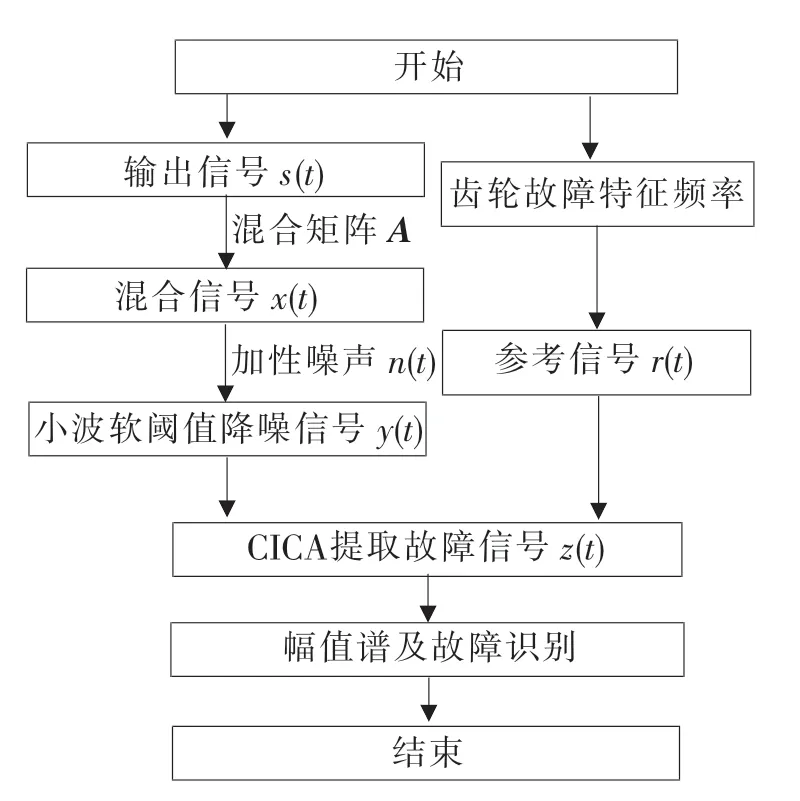
图1 流程图

图2 源信号及幅值谱

式中，s1为随机噪声信号；randn（·）为Matlab软件中产生随机噪声信号函数，N 为信号样本点数；s2为模拟无故障行星传动的啮合振动信号，啮合频率f2＝530 Hz，调制频率f1＝5.3 Hz为行星架旋转频率，θ1＝0；s3为模拟行星齿轮故障低频调制信号，啮合频率为f4＝93 Hz，低频调制频率为f3＝1.5 Hz，θ2＝0；s4为频率f5＝20 Hz的正弦信号。图2为仿真源信号及对应幅值谱。

对源信号加入不同的随机噪声和脉冲噪声，分别得到不同信噪比的信号a，由于篇幅有限，以加噪后信噪比为-20 dB的信号说明，图3为加噪后的信号波形图及对应幅值谱。

按照式（4）的混合模型，将加噪后信号进行线性瞬时混合，得到的4个混合信号时域波形如图4所示，可以看到其波形十分的杂乱。

图3 加噪后信号及幅值谱

图4 混合信号时域波形

为了形成对比，分别对混合信号进行直接CICA 信噪分离和小波软阈值预处理后的CICA 信噪分离。此时设定源信号s3为所要提取的期望信号。现对混合信号直接CICA 信噪分离得到图5。对混合信号进行小波软阈值预处理后的CICA 信噪分离得到图6。

图5 CICA提取的信号分量及幅值谱

图6 本文方法提取信号分量及幅值谱

对比图5和图6，同样正确的参考信号，图6经过小波软阈值预处理提取信号y3′时域波形与源信号s3十分相似，而其幅值谱可以看到频率93 Hz及其调制频率1．5 Hz产生的边频带，图5的提取信号y3及其幅值谱看不出任何特征及特征频率，杂乱无章。由此表明提出的方法可以正确地提取出期望的信号。

为了定量的说明此方法的优越性和有效性，应用信噪比SNR 和均方误差MSE 来评价算法的去噪效果，对应的表达式为

式中，Si为源信号；S′i为降噪后信号。

源信号加噪后信噪比为-20 dB，分别对故障信号计算仅用CICA 算法和本文方法处理后信号的SNR 和MSE，结果如表1所示，对比可知提出的算法的优越性和有效性，降噪上和性能指标都优于仅用CICA 算法。

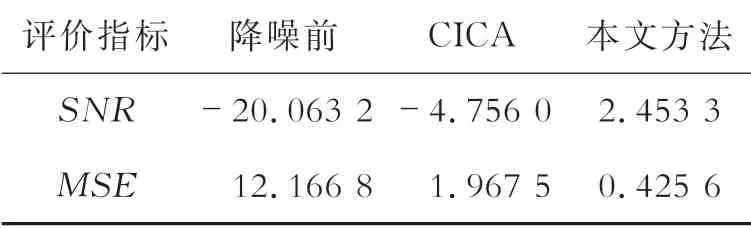
表1 性能指标数据对比

5 实测数据实验

为验证此方法对实际测试信号的有效性，采用SpectraQuest公司设计的可模拟工业动力传动的故障诊断综合实验台（DDS）进行实验分析，见图7。该实验台动力传动系统由1个1级行星齿轮箱，1个2级平行轴齿轮箱，1个轴承负载和1个可编程的磁力制动器组成，齿轮箱的传动系统如图8所示。

图7 DDS实验台

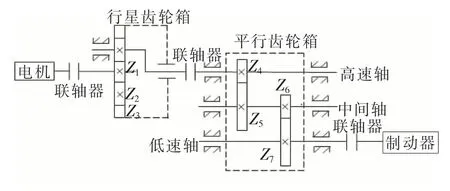
图8 齿轮箱传动系统图

研究将齿轮局部故障设置在定轴齿轮箱的输出级Z6／Z7的主动轮Z6（＝36）位置，如图9所示的位置，其它位置齿轮（含行星齿轮箱）及所有轴承均无故障。定轴齿轮箱齿轮Z6的单一故障设置为局部断齿障，其中断齿的宽度约为齿宽的30%，如图10所示；电机输入转速为40 Hz（2 400 r／min），传递到平行齿轮箱中间轴的转频为2．537 Hz，齿数为36，啮合频率为91．35 Hz。利用DASP数据采集仪采集数据，采样频率为5 120 Hz，总采样时长为10 s，截取其中2 s数据进行分析。

图9 故障齿轮位置

图10 局部断齿的齿轮Z 6

采集齿轮箱三通道的振动数据，时域波形及其幅值谱如图11和图12所示。从幅值谱上可以看到明显峰值40．35 Hz、40．4 Hz及40．05 Hz，接近电机输入转频40 Hz，还可以看到接近中间轴上齿轮的啮合频率92．25 Hz和92．05 Hz的峰值，但是边频带不明显，还有其它频率的影响，很难判断齿轮故障。

图11 齿轮箱实测信号波形

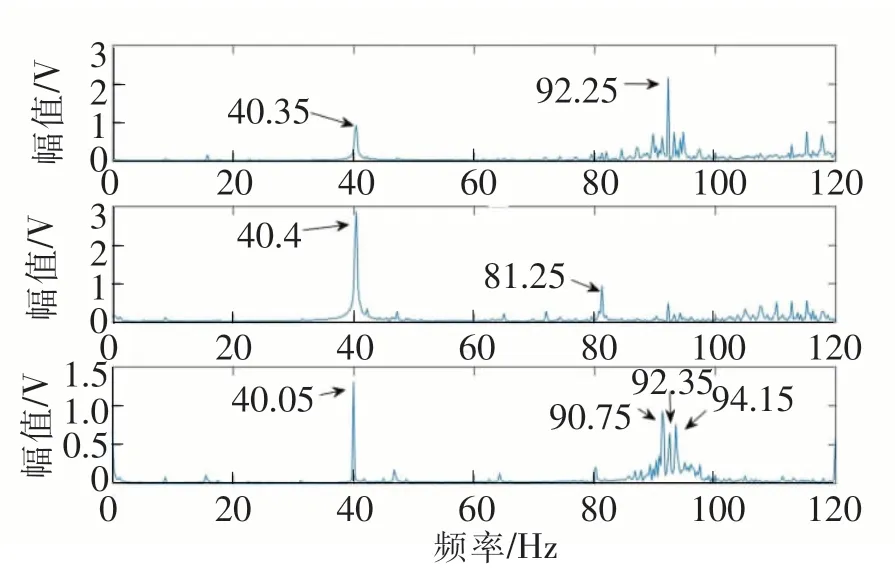
图12 齿轮箱实测信号幅值谱

以91．35 Hz为特征频率构建的参考信号r2，取阈值ξ＝1.5，未经小波软阈值降噪预处理时，仅用CICA 方法对图11所示的局部断齿故障测量信号直接提取的结果如图13所示，图14为提取信号y2的幅值谱，显然，提取的结果不理想，时域波形明显周期冲击成分不明显，幅值谱中电机的频率影响太大，并且齿轮故障边频带也不明显，不能说明齿轮故障。

图13 CICA提取的故障信号

以本文提出的小波阈值降噪与CICA 结合方法对信号进行处理分析，所提取的时域故障信号及其幅值谱，如图15和图16所示，参考信号r2相同，并且阈值同样ξ＝1.5，经过小波软阈值预处理过后，提取的时域波形可以明显看出冲击成分，信号降噪效果明显；图16的幅值谱中可清楚观察到故障齿轮的啮合频率（理论值91．35 Hz）及其两侧被转频2．53 Hz调制的边频。由此可见，该方法可实现齿轮箱中齿轮故障的分离，突出了齿轮的故障特征，效果十分明显。

图14 CICA提取的故障信号幅值谱

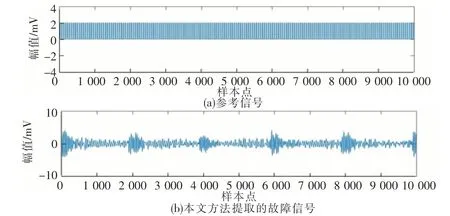
图15 本文方法提取的故障信号

6 结论

图16 本文方法提取的故障信号幅值谱

针对齿轮箱中齿轮故障提出了基于小波阈值和CICA 算法，小波阈值可以有效地对信号降噪、滤波，而CICA 可通过建立参考信号，将特定的故障分量分离出来，克服了ICA 方法的不确定性问题。将2种方法相结合，实现在强噪声背景下对齿轮局部故障的分离提取，适用于齿轮故障的诊断并通过具体的仿真和实验证明了该方法的有效性和实用性，为在强噪声下齿轮箱中齿轮故障提供新的诊断方法。