基于AHP和模糊集值统计的公路桥梁方案比选研究

杨青山，刘世忠，郑 璐

（1.兰州交通大学，甘肃 兰州 730070；2.陇东学院，甘肃 庆阳 745000）

0 引 言

桥梁型式复杂多样，除了跨越能力很强的悬索桥、斜拉桥、拱桥之外，仅应用最广的梁式桥也可以细分为简支梁、简支-连续梁、连续梁和连续刚构等多种形式。公路穿越地形通常较为复杂，如何根据具体的地形、水文、地质环境以及路线要求确定合理的桥梁选型方案，需要考虑众多因素。这些因素既包括了桥梁的跨越能力（布跨方案）、使用性能等反映桥梁功能特性的因素；也包括了桥梁本体造价、施工难度及需采取的专项措施等经济因素；同时还需考虑环保、自然景观等外部客观要求。在确定方案的初期，以上列举的因素大都只能定性描述，而且因为影响因素众多，各因素之间也存在互相耦合的情况，很难从多个备选方案中直接选出相对最优者。现行的桥梁选型通常是根据调查分析与估算列出待选方案的技术、经济指标凭设计人员的经验确定。这种方法受主观因素影响较大，评价过程繁琐，优选结果公认度差［1-3］。

桥梁方案选型应该建立一套科学化的评估标准体系。这套体系应简明规范、操作性强。

1 建立桥梁选型评价目标体系

《公路桥涵设计通用规范》中要求，桥梁设计应符合安全、耐久、适用、环保、经济和美观的原则。本文选取“结构体系”“施工措施”“工期”“跨径”“运营养护”“桥梁造价”6 个要素作为桥梁方案选型的第二级准则层，建立如图1 所示的综合评价层级体系［4-6］。

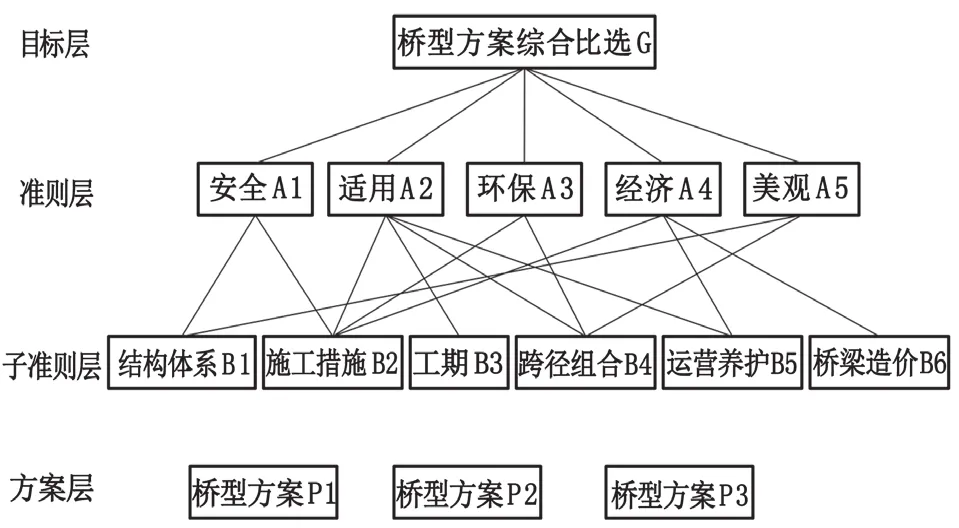
图1 桥梁方案选型综合评价层级体系

2 构造多级判断矩阵

对每一层次的各因素关于上一层中某一因素的重要性进行两两比较，构造判断矩阵。 针对图1 所示的层次体系通过专家打分，可构造准则层 A 相对于目标层 G 的重要性判断矩阵如下。

同理构造子准则层相对于准则层的重要性判断矩阵，其中 B1，B2相对于 A1的重要性判断矩阵为 A1；B2，B3，B4，B5相对于 A2的重要性判断矩阵为 A2；B2，B4相对于 A3的重要性判断矩阵为 A3；B2，B5，B6相对于 A4的重要性判断矩阵为 A4；B1，B4相对于 A5的重要性判断矩阵为 A5。

通过计算得判断矩阵 G 的最大特征值相应的特征向量 W=（0.393，0.279，0.067，0.216，0.046）T；A1特征向量W1=（0.833，0.167）T；A2特征向量 W2=（0.107，0.133，0.609，0.151）T；A3特征向量 W3=（0.333，0.667）T；A4特征值 W4=（0.115，0.182，0.703）T；A5特征向量 W5=（0.667，0.333）T；以上特征向量均满足一致性检验。

再考虑子准则层中各因素 B1～B6关于 G 的权重若记为 c1，c2，…，c6，则：

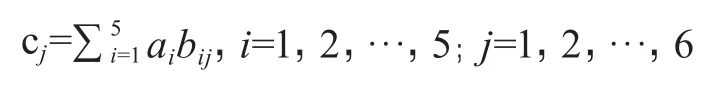
其中，（a1，a2，a3，a4，a5）=（0.393，0.279，0.067，0.216，0.046），记此向量为 A；bij为Bj关于Ai的权重，其组成的矩阵记为：

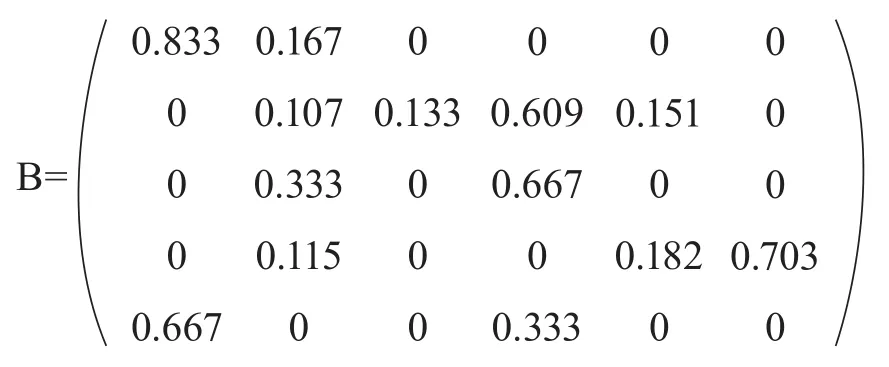
层次总排序为：

AB=（0.3581，0.1426，0.0371，0.2299，0.0814，0.1518）

且满足一致性检验，即桥梁结构体系、施工措施因素、施工工期、桥梁跨径组合、运营养护、桥梁造价关于桥梁方案选型综合评价的权重如矩阵 AB。

3 桥型方案评估指标评价模糊集值统计

对于具体桥梁方案的子准则层评价指标Bi，由评估专家pj依据其评估标准和对各指标有关情况的了解给出一个特征值区间［aij，bij］，由此构成一个集值统计系列：［ai1，bi1］，［ai2，bi2］，…，［aij，bij］，…，［aiq，biq］。

评价指标的特征值可按 式（1）计算。

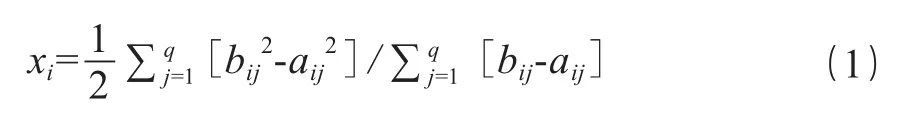
若在评分过程中考虑各个专家的学历、职称、从事本行业的工龄等自然情况，设每位专家自身的权值为k，则有评价指标特征值如式（2）所示。

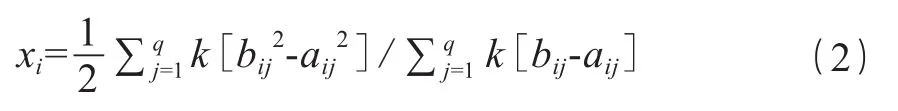
得到各指标特征值后，再分别与其对应的权重相乘后相加得到具体桥梁方案的总体评估得分，

通过不同方案总体评估得分的比较即可获得比选结果。

4 桥型方案比选实例

利用前述评估模型，假定有 3 位专家对 228 国道乐清乐成至黄花段工程 100 m 以上长大桥几种方案进行评估打分，选出最终方案。对于长度在 100 m 以上的长大桥梁，一般多采用 20、25、30 m 标准跨径，上部结构一般有组合箱梁和 T 梁两种；此项目桥梁多为海滨滩涂路段，桥址地质条件较差、计算桩长较长。下部结构均按平均柱高 10 m、桩长 55 m 考虑。上部结构对组合箱梁和 T 型梁两种结构形式分别采用一联 6×20 m、5×25 m、4×30 m 进行综合比选，如表1 所示。

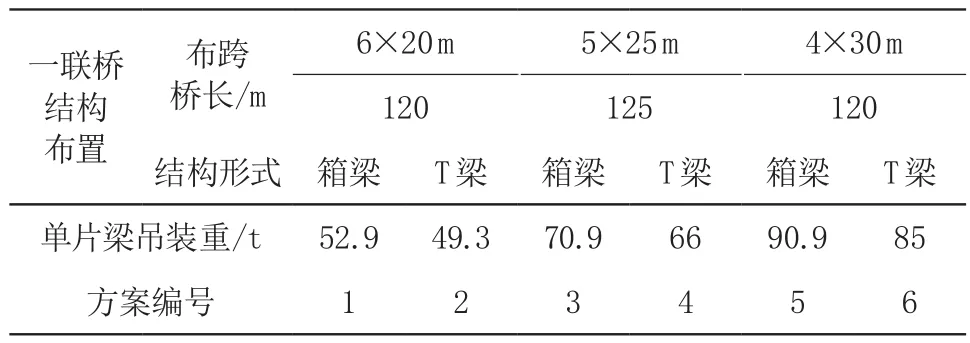
表1 各方案一联桥结构布置形式

方案 1～6 评分结果如表2～7 所示，为专家针对各指标逐一评分后，按方案汇总。

各方案按评价指标得分汇总如表8 所示。

通过各方案的得分对比，选择方案 6 作为最终方案。本例中各方案之间的得分差别较小。因为几个方案中“结构体系”和“跨径组合”存在两两相同的情况，这两项所占权重较大，分数差距不易拉开。

表2 方案 1 评分结果

表3 方案 2 评分结果

表4 方案 3 评分结果

表5 方案 4 评分结果

表6 方案 5 评分结果

表7 方案 6 评分结果

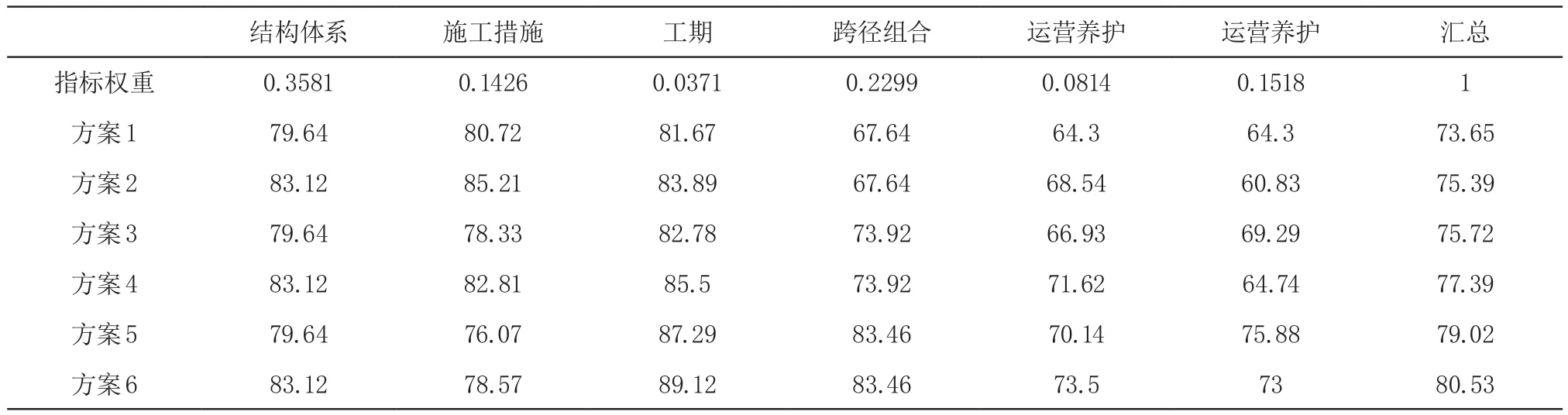
表8 方案比选结果汇总

5 结 语

本文提出了使用多层次分析法和模糊集值统计法结合进行桥梁方案比选的思路，即先用多层次分析法建立桥梁方案比选的评价指标，以判断矩阵的运算过程确定各指标权重；再利用模糊集值统计的方法进行具体方案的专家评分区间；最终得出各方案评分。这种方法是一种定性与定量相结合的评价方法，提高了桥梁方案决策的科学性和合理性。