动车组周转、到发线运用和接发车进路排列方案的综合优化研究

郑亚晶，李雨恒，李耀辉

（华南理工大学 土木与交通学院，广东 广州 510640）

自2008年8月1日中国第一条350 km/h的高速铁路——京津城际铁路开通运营以来，高速铁路在中国大陆发展迅猛. 而随着高速铁路网的完善，动车组的运用与周转问题也受到越来越多的学者的关注.高速铁路动车组周转问题类似于传统的机车周转问题，传统的机车周转问题研究工作主要可分为3类：(1) 将接车周转图的人工勾画方法进行扩展[1]；(2) 利用图论中的网络流理论解决机车周转问题[2-4]；(3) 利用运筹学中的指派问题的思路解决机车周转问题[5-6].我国动车组周转问题最早开始于赵鹏1997年的研究[7]，其构造的动车组不固定区段使用条件下的动车组周转优化模型成为这一领域的研究基础，之后不少学者在考虑检修[8]、空车调度[9]以及周期性[10]等基础上进一步丰富了此领域的理论.

以上成果都是从动车组运用的角度来研究动车组周转问题，而在实际工作中，动车组的周转工作是依托车站的到发线实现的. 史峰[11]率先将动车组周转和到发线运用结合起来对列车运行图进行了优化. 虽然该成果的目标是运行图优化，但无疑为动车组周转问题提供了新的思考角度. 本文就是在这一思路的启发下，结合文献[12]中到发线运用和接发车进路排列方案综合优化的方法，提出了动车组周转、到发线运用和接发车进路排列方案综合优化方法.

1 问题分析及符号定义

动车组周转实质是车列担任不同运输任务的接续关系，其可在运行图上表示为连接不同运行线间的周转线(如图1(a)所示). 通常在周转图上，为避免周转线之间的重叠，会给有重叠时间的不同周转线不同的偏移量，若将这些不同的偏移量与车站的到发线相对应，显然就可以将周转图和到发线运用联系起来(如图1(b)所示).

另一个方面，列车对到发线的占用时间是从列车接入该到发线的接车进路启用开始到列车发车出清到发线为止. 而对于同一条到发线来说，咽喉区往往存在不止一条接发车进路的径路方式. 如何配合到发线的运用方案对列车通过咽喉区进路的径路进行优化，是本文在考虑动车组周转的同时力求兼顾的问题.

为简便起见，本文的研究基于以下几个前提：(1) 目标车站均为贯通式车站且仅有2个咽喉区；(2) 高铁列车在整个过程中不进行解挂或连挂作业；(3) 所有列车的长度都相等且列车在股道上停靠，不会侵入任何咽喉道岔的范围.

一个车站的到发线在运行图中有3个可能的位置(如图2所示)：(1) 在周转图的最上方，本文中称之为顶部车站；(2) 在周转图的最下方，本文中称之为底部车站；(3) 在周转图的中间，本文称之为中部车站. 根据实际情况不同，中部车站可能不存在，也可能存在多个，本文以一个中部车站为例进行相关研究.

定义 φ表示这3个位置的车站，在本文中，φ 值的0、1、2分别对应顶部车站、底部车站和中部车站(若中间车站有2个或以上，φ 值可进一步增加相应数值).将车站 φ的2个咽喉按图2的方位分别定义为上端咽喉和下端咽喉.

本文将每个车站的到发线按图2所示分别顺次编号为1、2、 ···、n，其不同编号对应车站不同的到发线股道.

图 1 周转线和到发线之间的关系Fig.1 The relation between turnover line and arrival-departure line

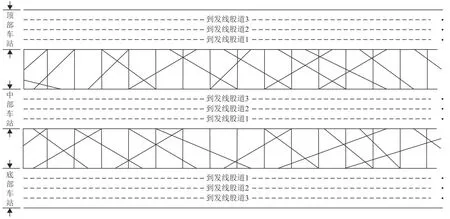
图 2 周转图中周转线的可勾画位置Fig.2 The delineable position of the connection line in the turnover graph

定义Kφ为车站φ 的到发线编号(按图2编号)集合，显然其元素kφ∈Kφ即代表了到发线的股道号，也代表着周转线的可勾画位置. 为增大模型的适用性，本文定义讨论的运行图并不限定为以24 h为周期的标准图，而是可以以任意截取的运行图时间段作为研究对象. 对于任意截取的一段列车运行图来说，由于不是所有的周转线连接的运行线都在截取的时间之内，因此有必要在图2所示的到发股道右方设置虚拟节点，替代某些周转线右侧连接的在截取时间之后的运行线. 本文作业之间的间隔时间利用符号⊙ 进行计算，该符号的含义如式(1)所示.

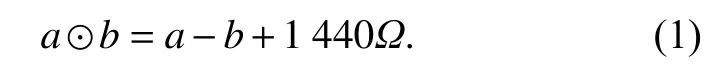
式(1)中Ω 表示b和a的日期天数差.

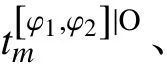
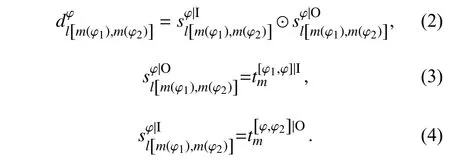
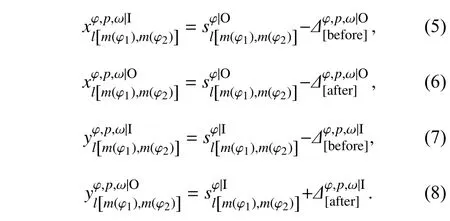
2 模型构建

2.1 与动车组周转有关的优化目标和约束

约束条件为每条运行线的起讫点均需连接且只连接1条周转线：

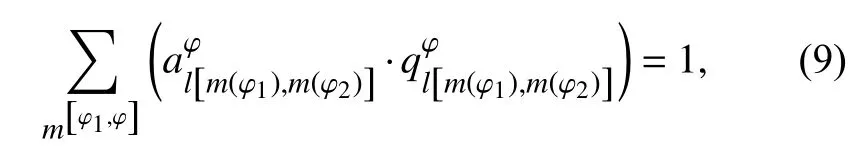
其中φ ≠φ2.

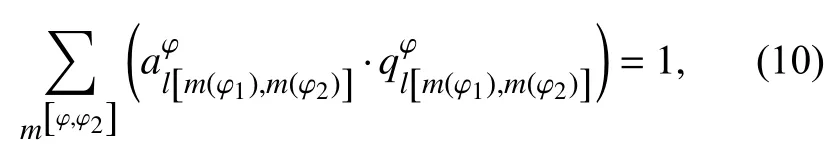
其中φ1≠φ.

优化目标为： (1) 运用动车组数最小：

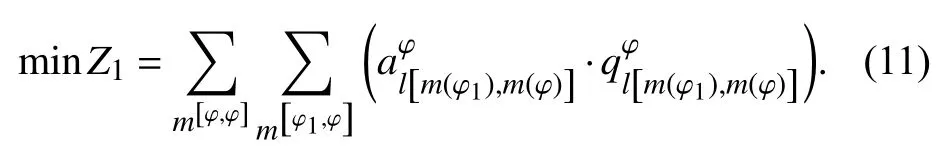
(2) 动车组在站总停留时间最短：

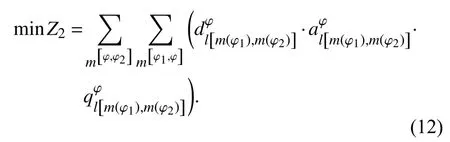
2.2 与到发线运用有关的优化目标和约束

约束条件为： (1) 每条实际周转线只能由1条股道实现：

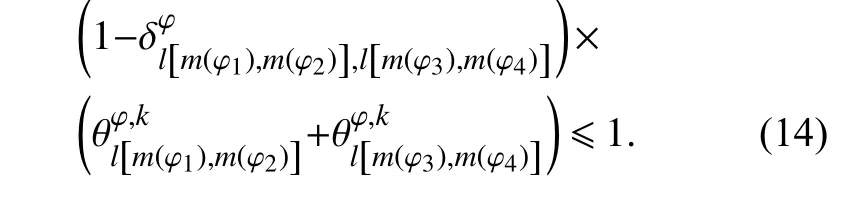
优化目标为到发线的效用最大：

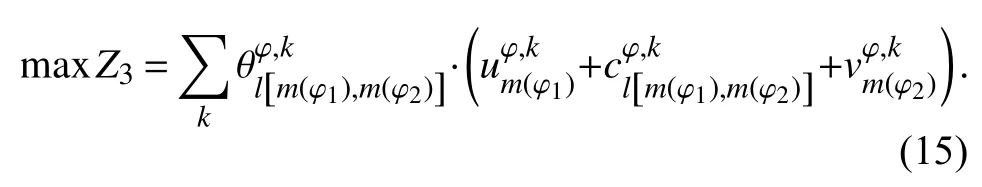
2.3 与接发车进路排列有关的优化目标和约束

约束条件为1个周转过程只能由1个进站进路和1个出站进路实现（以车站φ靠近车站φ1端为车站φ的上端为例，其他情况与之类似）：

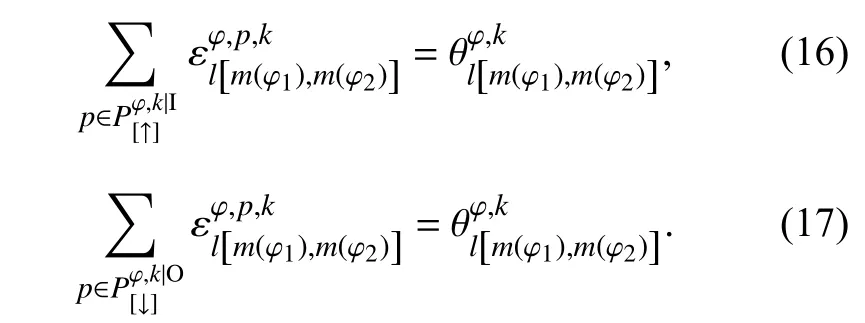
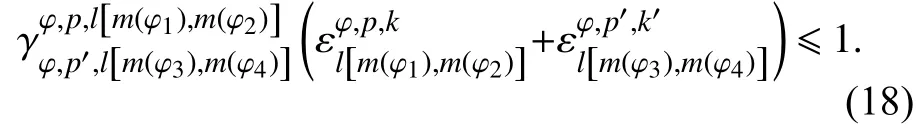
优化目标为总进路的走行路程最少：

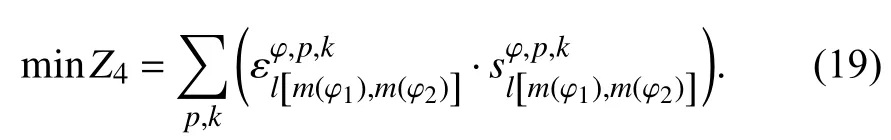
2.4 总体模型和求解

虽然以上的3组优化目标和约束可以看成3个优先层次模型，但并不能据此按顺序分层求解，否则有可能会出现低层模型在高层模型的最优解条件下无解的情况，因此，本文的模型为一个整体模型，其中优化目标为式(11)、(12)、(15)、(19)，约束条件为式(9)、(10)、(13)、(14)、(16)、(17)、(18). 4个目标的优先级为Z1＞Z2＞Z3＞Z4. 这是一个多目标0-1型整数线性规划，可以利用商业优化软件，例如ILOG CPLEX或Lingo进行求解. 本文的整个求解过程是利用C#多次调用ILOG CPLEX实现.

3 算例

以某高铁车站B站18:00～24:00的列车时刻表为例，车站A和C为车站B的相邻车站，车站A、B和B、C之间的列车时刻表如表1所示，B站的平面示意图如图3所示.

根据列车类型以及到发线固定使用方案，确定列车占用各到发线和起停车的效用值如表2所示.

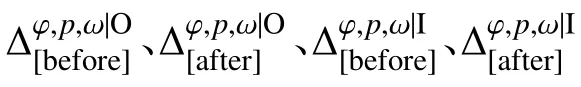
4 结论

(1) 本文提出了动车组周转、到发线运用和接发车进路排列综合优化模型，可以在获得动车组周转的同时，得到到发线运用方案和接发车进路排列方案，这既精简了编制相关方案的工作流程，又确保了动车组周转方案和到发线运用方案的可应用性.

表 1 列车时刻表Table 1 Train timetable

图 3 B站车站平面图示意Fig.3 The plane graphic representation of station B

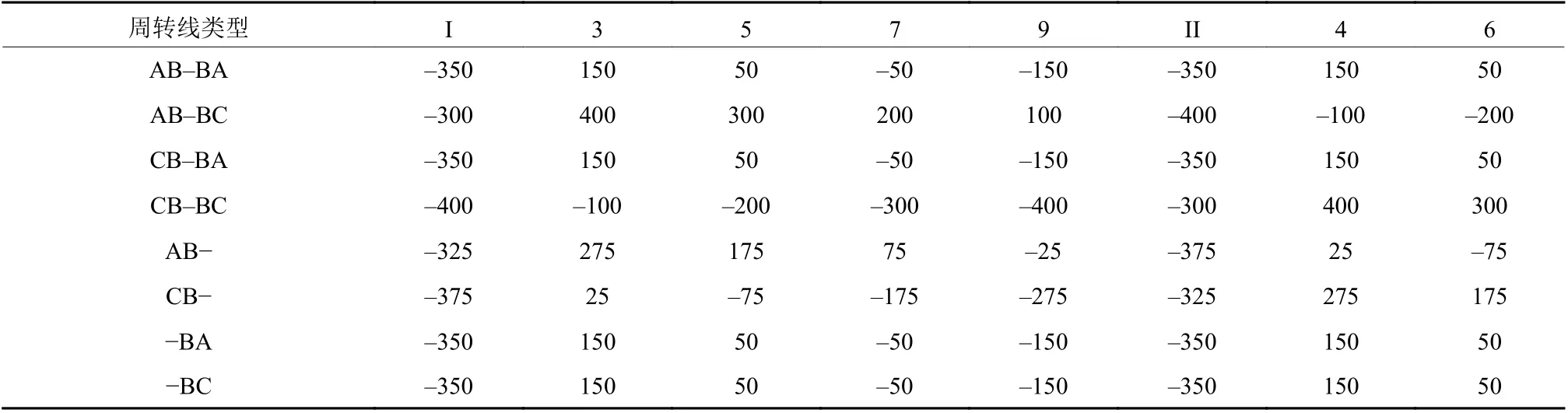
表 2 动车组停车效用值Table 2 Parking utility value of multiple unit

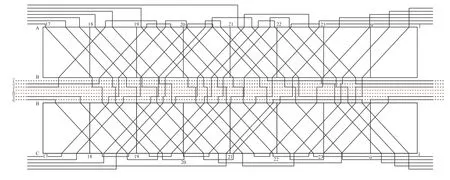
图 4 周转方案和B站股道运用图Fig.4 Turnover plan and track operation diagram of station B

表 3 接发车进路方案Table 3 Receiving and departing route scheme

(2) 本文模型以所有高速列车的车长均为定值且任意轨道停靠列车都不会影响到咽喉区道岔为前提. 若动车组长度不一致，可增加相应股道和动车组的匹配约束.

(3) 本文模型以高速铁路列车为对象，若要用于非动车组类列车的机车和动车组周转、到发线运用以及接发车进路排列方法则需对模型进行较大的变动，相关内容有待进一步研究.

(4) 本文仅初步分析了动车组周转、到发线运用和接发列车进路排列方案的综合优化方法，对于动车组的解编、列车的检修以及相关方案与乘务计划的匹配等还有待进一步研究.