基于OMP算法的舞动监测系统

刘 豫，刘佳鑫，贾云飞，王献策，冯恺鹏

(1.南京理工大学 机械工程学院，江苏 南京 210094；2.国网辽宁省电力有限公司电力科学研究院，辽宁 沈阳 110006)

0 引 言

随着社会的发展，对电力的需要日益增长，我国电网规模也在不断扩大.高压架空输电线路作为电网的重要组成部分，地域分布广泛，所经地区的地形、地质、气象等环境复杂.近年来，我国受极端天气影响，输电线路覆冰、舞动事故越来越频繁，并呈逐年增加的趋势，严重影响了电网的安全和稳定运行[1-2].大型输电线路跨越的地理位置大，途径区域多，在一定气候条件下，极易发生舞动事故，导线一旦发生舞动会造成线路跳闸、断线、绝缘子碰撞破损、塔材螺栓松动甚至倒塌等严重事故[3-4].目前国内外对舞动监测主要有远程图像监控和舞动在线监测装置两种手段[5-6].远程图像监控得到的舞动图片通过在杆塔上装设摄像头，采集舞动图像信息进行分析，但该方法无法提供舞动数据进行科学分析[7]；传统舞动在线监测装置利用布置于导线上的加速度传感器来采集导线的状态信息，舞动还原精度取决于监测单元的数目，对于大档距线路的监测往往使用大量的监测单元，对线路存在较大的力学特性影响，本文研究了基于OMP算法的舞动监测系统，利用少量监测单元重建舞动信号，减小监测系统对线路力学特性的影响，并节约了监测成本.

1 基于OMP算法的舞动监测系统构成

基于惯性传感器的舞动监测系统整体结构如图1所示，系统分为舞动监测装置，通信主系统和上位机系统3个部分.舞动监测装置由传感器采集模块、信号调理模块、STM32控制模块、4G通信模块、电源模块组成，负责舞动数据的采集、信息的解算和打包发送；通信主系统由STM32主控模块，4G通信模块组成，负责给各个监测装置提供同步采集信号，将接收到的导线位移数据发送给上位机终端.上位机终端是算法处理中心，使用OMP算法重建舞动信号，完成对舞动信号的显示与保存.

工作时舞动监测装置安装在线路上，等待STM32主控模块发出采集命令，当接收到采集命令时开始实时采集输电线路舞动信息，采集的信息经硬件低通滤波去除高频噪声传输给STM32控制模块进行加速度解算、去直流、积分和去趋势项的计算，得到导线位移数据.STM32控制模块将计算好的数据打包，通过4G发送模块和基站对数据进行远距离传输，STM32主控模块接收到来自基站的信号后将数据发送给上位机，上位机根据算法重建舞动信息并显示和保存.

2 基于OMP算法的舞动监测系统研究

2.1 系统硬件设计

舞动监测装置如图2 所示，由MPU9250传感器、信号调理模块、STM32计算模块和4G通信模块组成.

图2 舞动监测装置组成示意图Fig.2 Composition sketch of galloping monitoring device

MPU9250传感器由 2 部分组成.一组是3轴加速度还有 3 轴陀螺仪；另一组是3轴磁力计AK8963.所以，MPU9250 是一款9轴运动跟踪装置.在本文中使用角加速度修正导线扭转产生的加速度误差，其具有测量范围大、精确度高、体积小、抗冲击能力强等优点；其传输速率快，集成电路总线(IIC)传输速率可达400 kHz/s，串行外设接口(SPI)传输速率可达20 MHz/s.陀螺仪的角速度测量范围最高达±2 000°/s,具有良好的动态响应特性，可满足多个加速度传感器同时采集的要求.MPU9250主要性能指标如表1 所示.信号经过数字低通滤波过后使用IIC方式与STM32计算模块相连.

表1 MPU9250性能指标Tab.1 MPU9250 performance indicators

微处理器选用STM32F103VET6，STM32外设丰富，数据处理能力强，舞动信号一般频率为0.1～3 Hz，本文将采样频率设为100 Hz，每次采样进入一次中断，负责将加速度信号处理成位移信号并发送出去，STM32和4G模块通过串口通信，处理完的数据通过4G通信模块可进行远距离的传输.

常用的无线通讯方式有WiFi、蓝牙、ZigBee、4G通信等，输电导线跨越大，对通信距离要求比较高，选用传输距离远，可靠性高的SIM7100C模块作为无线传输模块.SIM7100C为4G通信模块，采用时分双工LTE-TDD技术，传输速率快，支持IIC和SPI两种连接方式.本文采用IIC方式与STM32芯片进行通信，通信速率可达400 kbit/s，数据传输误码率低，同时在未工作时SIM7100C模块进入休眠模式，耗流小于5 mA，功耗极低，可实现长时间的舞动监测.

上位机系统为PC机，接收采集到的舞动数据，并对舞动信息进行重建、显示和存储.

2.2 基于OMP算法的监测系统设计

导线舞动是导线沿圆周方向覆冰不均匀的架空导线在侧向风力作用下产生的低频、大幅度自激振动现象[8].其摆动幅度随风载荷的变大而变大，最后在风载荷和线路系统自身阻尼的作用下，舞动幅度逐渐趋于稳定，当线路覆冰情况，线路材质，档距和线路结构不同，或风载荷和风攻角不同时，导线产生共振的频率也不同，舞动稳定下来时的特征也不同，常见的有1个半波，2个半波和3个半波，4个半波的模态.如图3 所示.

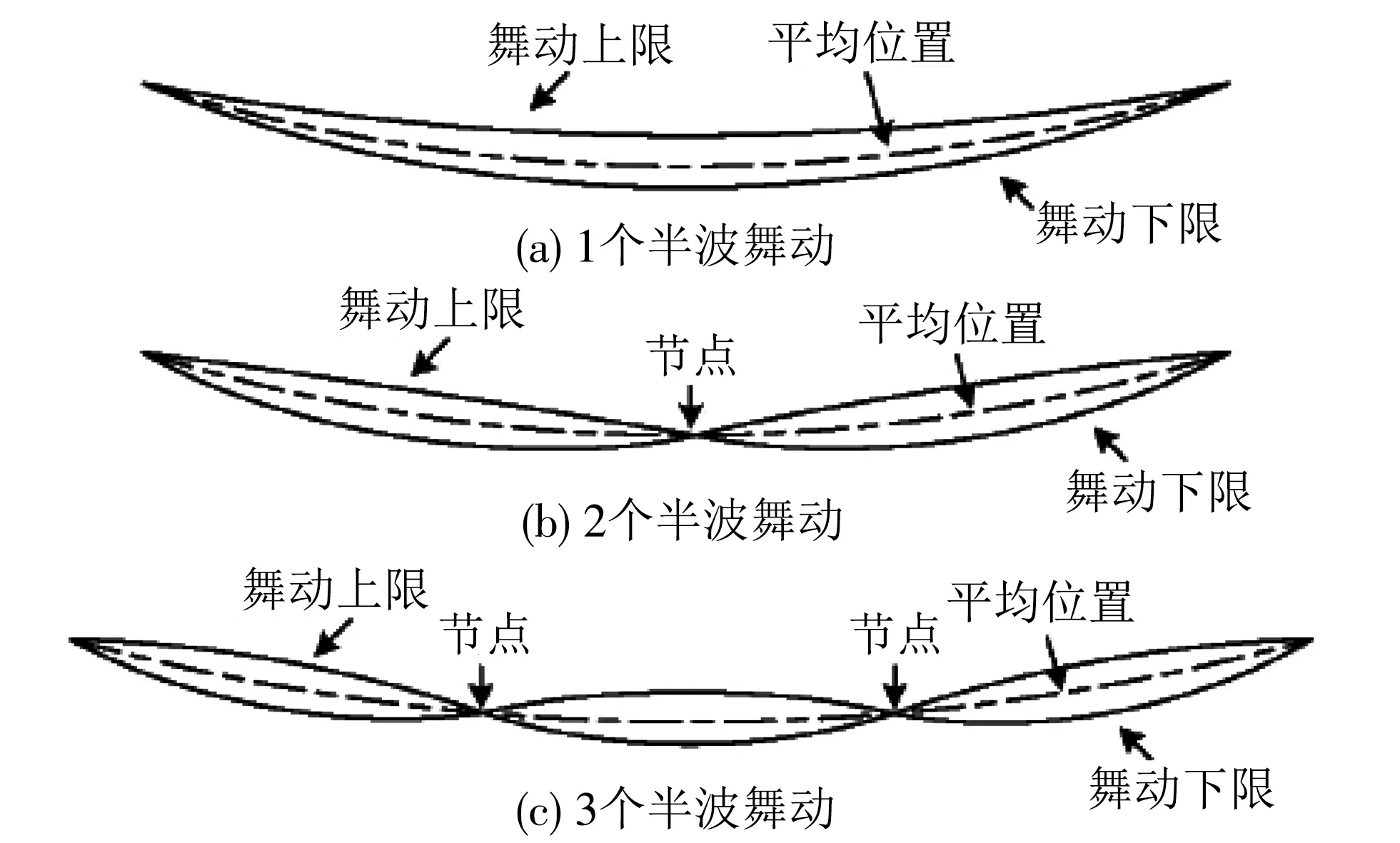
图3 线路舞动模态Fig.3 Type of line galloping

导线舞动稳定后舞动波导线波方程的数学表达式为[9]

式中：a0(t)为线路舞动的最大幅值；ω为舞动传播速度；t为时间；n为半波数；l为档距.振动方程表示了不同时刻不同弧长下的舞动振动形态，取t为定值可观测某一时刻线路舞动随弧长的变化[9].

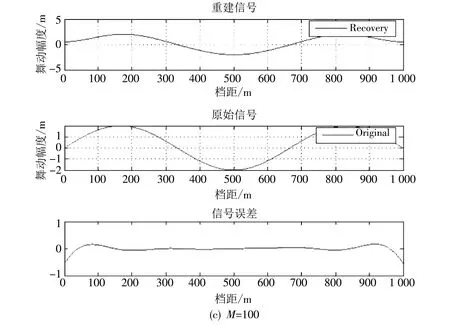
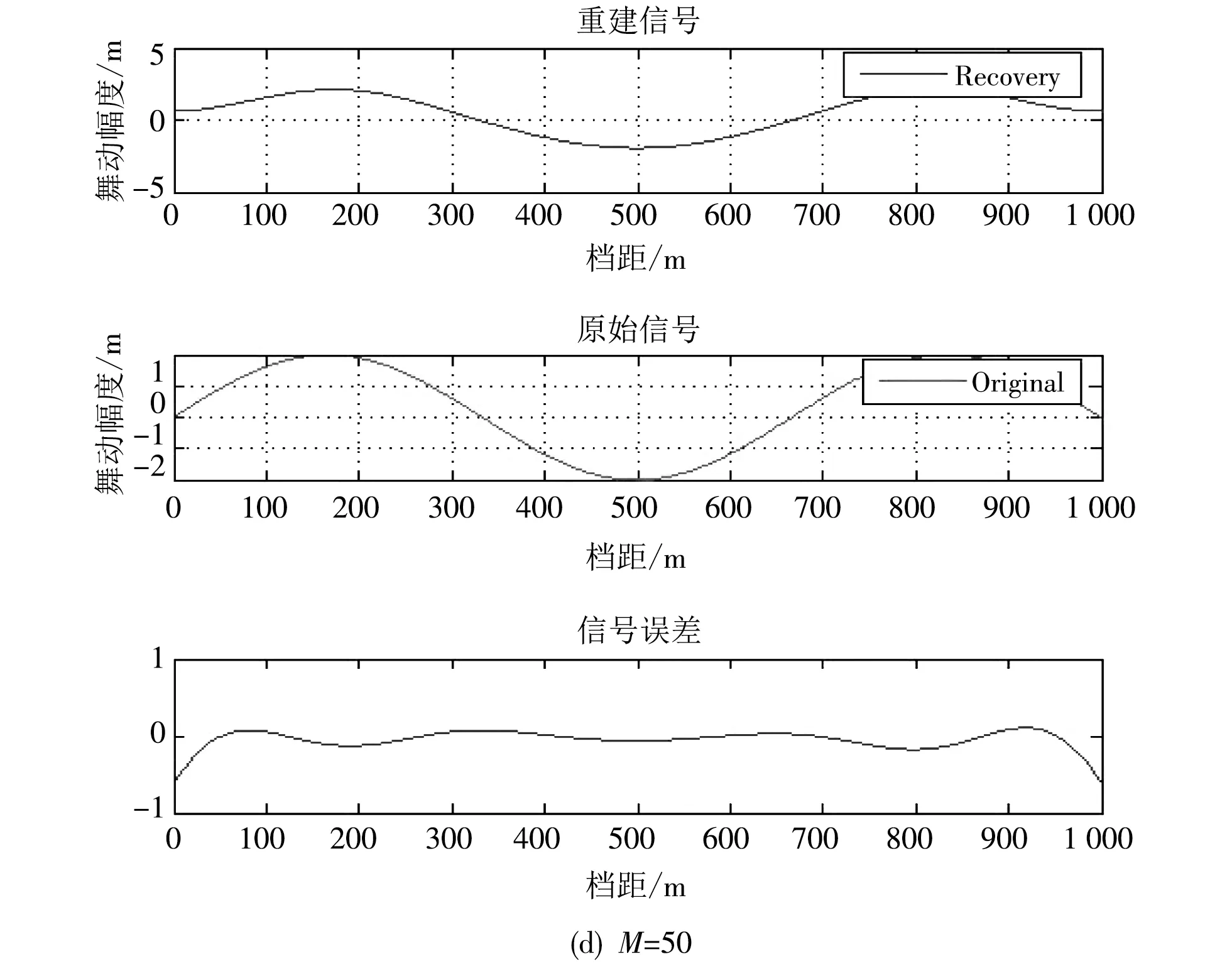
设计一个大小为M×N(K≪M

y=ΦX=ΦΨα=Aα,

式中：y为信号x的观测值；A为传感矩阵，由采样矩阵和稀疏基组成，采样矩阵和稀疏矩阵要求相互独立，即二者的行和列不能相互表示，本文稀疏基采用过完备的傅里叶基，设计采样矩阵为服从高斯分布的M×N阶矩阵，二者相互独立性较好，且采样矩阵满足矩阵的受限等距性质(RIP)，可保证信号重构的要求，过完备的傅里叶字典是由频率标识的正弦波形的集合

信号的重构通过如下优化问题解算：

s.t.y=Φx=Aα.

OMP算法在冗余字典里选择到最为匹配的原子后，将所选原子利用Gram-Schmidt正交化方法进行正交化处理，再将信号在这些正交原子构成的空间上投影，得到信号在各个已选原子上的分量和残余分量；然后用相同的方法分解残余分量.经过M次的迭代分解，原信号被分解为M个原子的线性组合.在每一步的分解中，所选取的最佳原子均满足一定条件，残余分量随着分解过程迅速衰减.这样经过有限次的迭代就可以收敛，用选取的少量原子就可以表示原始信号.

正交匹配追踪便是通过将舞动信号余项投影到{grm}0≤p

D={gr}r∈Γ是由|Γ|>N个单位向量所形成的过完备字典，选择过完备的傅里叶基作为稀疏基.

然后利用Gram-Schmidt算法将grm关于{grm}0≤p

当迭代到第K次时，对所有的向量投影求和可得信号的稀疏表示

对稀疏后的信号进行OMP算法运算解算得到最佳的表示系数α并重建得到舞动信息.

以3个半波的导线舞动模态，1 000 m档距的导线作为研究对象进行仿真，假设导线舞动最大幅值为2 m，当时间t取0.5π，即导线舞动幅值处于最大时，此时其导线舞动波形及幅频特性如图4 所示.

图4 3个半波模态的导线舞动波形及幅频特性Fig.4 Wire galloping waveforms and amplitude-frequency characteristics of three half-wave modes

由图4 可知，信号在过完备傅里叶基构成的空间下稀疏度K=2，取信号长度N=1 001，使用OMP算法对其进行数据的压缩还原，当取观测点数M分别为500，200,100,50 4种情况时，取得的信号还原效果如图5 所示.

图5 不同观测点数下的舞动信息重建Fig.5 Reconstruction of galloping information under different observation points

信号重建的逼近误差采用原始信号减去重建信号的误差信号的二范数来估计，具体误差如表2 所示.

如图6 所示，除去端点误差外，当M=50时，最大幅值误差为0.188 2 m，相对误差为9.41%.在误差允许范围内可认为当观测点数目为50时，重建出的1 000 m档距舞动曲线导线波效果可靠，OMP算法效果良好.

表2 不同观测点数的逼近误差Tab.2 Approximation errors of different observation points

图6 M=50时最大重建幅值误差Fig.6 Maximum reconstruction amplitude error at M=50

3 结束语

本文为简化输电线路舞动监测的复杂度，将OMP算法应用在输电线路监测上，证明了系统的稳定性，并通过Matlab的仿真功能，验证了该算法在监测点数较少时仍拥有较优异的舞动信号重建功能，并用STM32与MPU9250设计了相应的硬件系统，从而完成了线路监测的优化.