基于座椅人机参数的列车座椅舒适度评价方法
2019-12-16支锦亦向泽锐徐笑非
王 金,支锦亦,2,向泽锐,2,李 然,2,徐笑非,2,闫 磊,徐 刚
(1.西南交通大学建筑与设计学院,四川 成都 610031;2.西南交通大学人机环境系统设计研究所,四川 成都610031;3.中车青岛四方机车车辆股份有限公司,山东 青岛 266000)
随着我国轨道交通的技术的发展,高速列车时速进入350 km/h时代,追求高品质的乘坐舒适性是伴随这一发展历程的必然要求[1].在高速列车乘坐舒适度研究中,座椅与乘客接触最多、应用最广,是体现车内品质、提升乘坐舒适度的重要载体[2],同时,座椅舒适度在高速列车乘坐舒适度中占有较大权重[3].
座椅舒适度评价方法有主观评价[4-5]、客观评价[6-8]和主客观评价相结合[9-13]3种.其中主观评价法通过对座椅各个部件或者各个人机接触面以及总体舒适度进行量表打分并统计,依据统计数据对座椅舒适程度进行量化分析;客观评价法通过借助外部设备测量被试相应身体部位的生理指标及物理指标;主客观相结合评价方法将主观舒适度评价和客观测量指标结合起来,分析其关联度.表1是3种研究方法的特点.
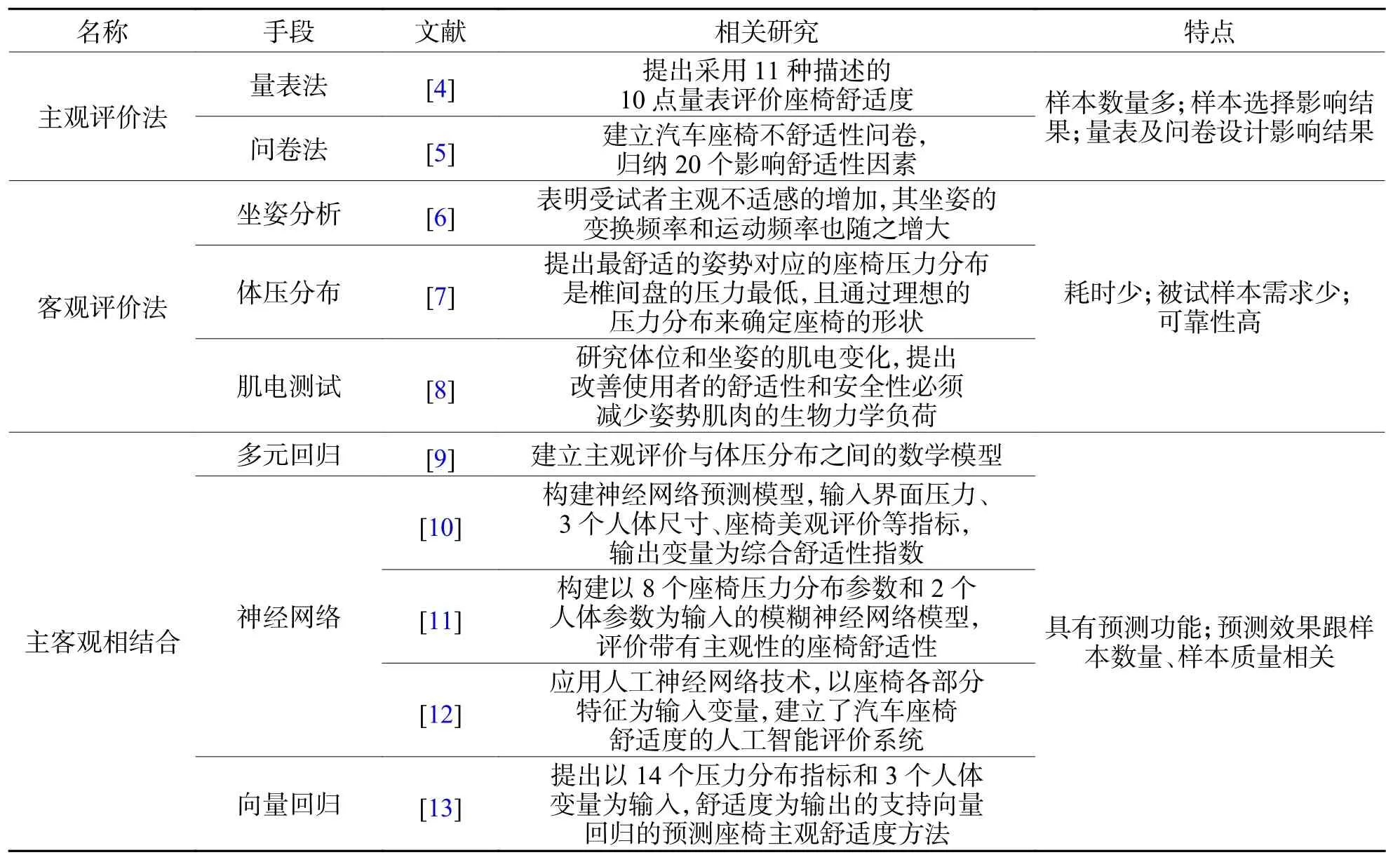
表 1 座椅舒适度评价方法及特点Tab.1 Methods and characteristics of seat comfort evaluation
通过分析现有满意度研究方法发现,通过满意度问卷来获得乘客对座椅局部或整体舒适度的评价,这种方法耗时,成本高,而且存在评价过程认真程度带来的评价信度问题,同时这种调查活动往往针对一个座椅的舒适度评价,或几个座椅的舒适度比较,对高速列车座椅舒适度评价缺乏预测意义,无益于降低再次进行座椅舒适度主观评价的工作量.在渐进学习理论看来,基于统计学来确定某一客观测量指标对应的舒适度评价,要求无穷大的样本量来支撑,在现实数据获取中,无穷大样本的获取以及有效性存在问题[13]。这就需要有恰当的关系模型来表达客观测量指标和主观舒适度评价之间的映射关系.传统的因子分析和多元回归分析等对两组之间的非线性关系考虑不足,与人的认知过程存在差异[14].
BP (back propagation)神经网络模型有很好的非线性逼近和自学习能力,在学习适当数量的自带答案的样本后可以实现从输入到输出的任意非线性映射,具有较好的预测效果.基于这些优点,目前,利用神经网络已经建立了汽车座椅压力分布与座椅舒适度之间关系的评价模型[15],构建了人体舒适度的短期负荷预测的模型[16].且神经网络的构建从探究参数的设置对预测效果的影响向输入指标的筛选和确定对预测效果的影响发展[11-12,15].将BP神经网络用于座椅舒适度预测,可以通过对座椅参数指标的输入直接得到舒适度评价输出,避免进行大量的问卷调查和统计分析,节省时间和成本.
本文利用MATLAB的newff函数构建BP神经网络,探究高速列车座椅人机几何参数和静态舒适度评分之间有效的非线性函数关系,并通过提取网络的权值和阈值来构建高速列车座椅人机几何参数和其静态舒适度评分之间的数学关系,以期通过输入座椅人机几何参数得到座椅静态舒适度输出.
1 列车座椅人机几何参数及评价方法
1.1 座椅人机几何参数指标
反映主观舒适度的座椅物理指标的选择需满足两个条件,其一指标有明确的物理意义,其二较好反映座椅物理参数和主观舒适性关系,即指标能从不同角度体现座椅的特征,特别是与乘坐舒适性关系密切的几何物理参数[17].有研究指出国内高速列车座椅静态舒适度研究集中在座椅尺寸的优化设计、材料、色彩等,但由于舒适度评价活动的主观性、评价对象及环境的差异性,以致广泛的座椅尺寸优化设计研究呈现的参考值却有所不同[18].因此研究高速列车座椅尺寸和舒适度之间关系用于指导高速列车座椅舒适度评价和寻求最优值都具有一定意义.
高速列车座椅的几何物理参数主要有座椅人机几何参数和曲面形态两类[19].座椅舒适度客观评价法的较多指标都是依据高速列车座椅几何物理参数与人体的一种适配关系.例如坐姿分析中通过改变脊柱、骨盆、腿和脚的受力力矩和夹角来调节身体各部位的负重关系,以达到舒适感[20].体压分布也是这种人体负荷关系在人椅接触面的呈现.鉴于曲面形态主要研究与人体曲线贴合程度,跟人机几何参数属于不同的参数类别,应该分开研究.因此本文将座椅人机几何参数作为物理指标来讨论与主观舒适度的关系.
高速列车座椅人机几何参数包括:座高、座宽、座深、靠背高、靠背宽、容膝距、靠背倾角、座间距这8个参数[21].
1.2 座椅人机几何参数舒适度权重计算
座椅人机几何参数对应舒适度权重评价具有模糊和不确定性,因此采用模糊评价方法,将座椅8项人机几何参数看作一个集合A={A1,A2,A3,A4,A5,A6,A7,A8},将A中的因素Ai相对于Aj的重要程度记为aij(i,j= 1,2,3,4,5,6,7,8),结合 saaty 的 1~9级重要性标度法将A中各因素相对于另一因素的重要程度进行比较,构建出模糊评价矩阵B.
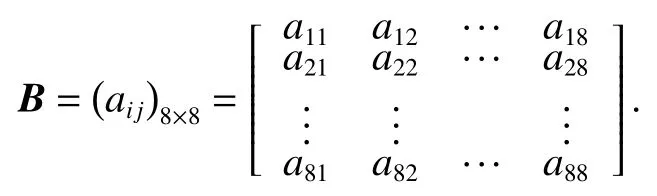
使用求和法计算矩阵B的特征向量的近似值W,即A中各因素权重,步骤如式(1).

式中:n为判断矩阵的阶数.
得到特征向量W=(w1,w2,···,w8),同时利用特征向量W的理论最大特征值λmax与n之差检验权重的一致性,指标包括一致性指标(CI)、一致性比率(CR),计算公式见式(2)和式(3).
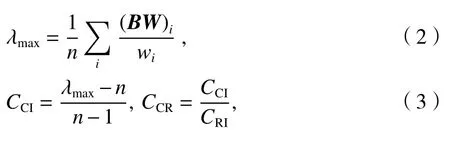
式中:CCI、CCR和CRI分别为一致性指标、一致性比率和随机一致性指标,其中,CRI= 1.41.当CCI< 0.1、CCR< 0.1时,判断矩阵一致性可接受,否则重新调整判断矩阵.
1.3 座椅人机几何参数的主观舒适度调查
采用7级满意度量表进行高速列车座椅舒适度调查,对不同高速列车座椅样本的人机几何参数每一项分别进行满意度打分,1分表示非常不满意,7分表示非常满意,获得高速列车座椅每一项人机几何参数的舒适度评分.
参与主观舒适度评价的被试为有高速列车一、二等座乘坐经历的普通健康乘客;人体尺寸覆盖5%~95%的人体百分位尺寸,且符合正态分布;被试人数采用简单随机样本量计算方法,根据研究需要的调查置信度和估计误差,求得被试人数最小值.
进行主观舒适度调查的高速列车座椅主要涉及高速列车一、二等座座椅和自制可调节实验椅,部分样本见图1.

图 1 高速列车座椅的部分样本Fig.1 Part of samples of high speed train seats
1.4 高速列车座椅静态舒适度计算
对获得的每个座椅样本的每一项人机几何参数舒适度进行评分,并计算该样本该项所有评分的均值;然后再根据座椅人机几何参数的权重计算出每一组座椅的静态舒适度评分, 即21组座椅中每一组座椅静态舒适度评分表示为

式中:wi为高速列车座椅人机几何参数的舒适度权重;
x为高速列车座椅样本组数(x= 1,2,···,21);
y为参与评价的被试人数(y= 1,2,···,p);
Dxiy为舒适度问卷调查中第x组样本中关于座椅人机几何参数i的第y个人的舒适度评分.
2 基于BP神经网络的舒适度评价模型
2.1 神经网络构建
利用MATLAB 神经网络工具箱中的newff函数来构建BP神经网络,并进行数据训练和验证.神经网络的训练需要较多的自带输入和输出的样本,样本的有效性和数量决定了网络训练的有效性.
神经网络输入参数为座椅样本的座高、座深、座宽、靠背高、靠背宽、容膝距、靠背倾角、座间距这8个座椅人机几何参数测量数据.神经网络的输出为该座椅样本的静态舒适度评分.
将不同座椅样本的人机几何参数测量数据和对应座椅样本的静态舒适度导入神经网络,设定和调试神经网络训练参数,并用不同于训练样本的座椅人机几何参数测量数据和对应座椅静态舒适度,对训练好的神经网络进行验证.
2.2 神经网络数学公式获取
为便于将训练得到的有效神经网络广泛用于高速列车座椅舒适度评价的预测,可将构建好的神经网络模型转化为可搭载于数学运算软件或者编程软件的数学表达公式.提取神经网络层级间权值和不同层阈值并代入式(5)、(6),构建神经网络的数学公式,实现高速列车座椅人机几何参数测量数值到座椅静态舒适度评分的输出.
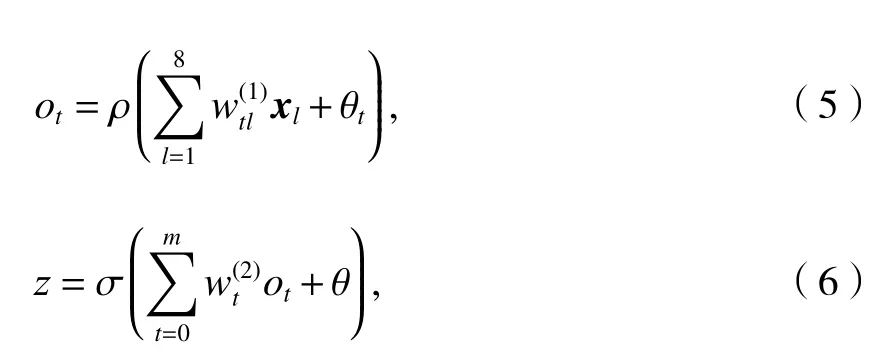
式中:xl= (x1,x2,··,x8)为输入变量;z为网络输出结果;ρ为隐含层传递函数;σ为输出层传递函数;θt为隐含层的神经元阈值;wtl(1)为输入层到隐含层的权值;θ为输出层的神经元阈值;wt(2)为隐含层到输出层的权值;m为隐含层节点数.
3 实例研究
3.1 数据获取
以文献[3-21]调研数据和相关高速列车座椅舒适度实车调研数据为例,挑选23组不同高速列车座椅样本的人机几何参数测量数据,以及每项参数对应的舒适度评分.通过专家对高速列车座椅8项人机几何参数相对重要性进行打分,构建模糊判断矩阵,通过式(1)计算得出高速列车座椅8项人机几何参数权重,见表2.

表 2 座椅人机几何参数舒适度权重Tab.2 Comfort weights of seat ergonomic parameters
通过式(2)、(3)计算得出λmax= 8.517;CCI=0.074;CCR= 0.052,且满足一致性检验标准CCI<0.1,CCR< 0.1,即判断矩阵一致性检验通过,座椅人机几何参数舒适度权重有效.
通过式(4)计算得出每一个座椅样本的静态舒适度.
3.2 神经网络构建
通过上述操作,获得包含高速列车座椅人机几何参数测量数据和对应座椅静态舒适度评分的有效数据23组,将其中的21组数据作为神经网络训练样本,将剩下两组样本(CHR2型一等座和二等座的座椅)[3]作为验证样本.
采用BP神经网络,隐含层的传递函数为logsig,输出层传递函数为purelin,最大迭代次数为10 000次,学习效率为0.1,目标误差为0.
比较11次不同隐含层和不同节点数训练结果误差均值和均方误差(表3),1个隐含层时13个节点数的误差均值和均方误差最小,2个隐含层时9个节点数的误差均值和均方误差最小.且1个隐含层13个节点数的误差均值和均方误差较2个隐含层9个节点数的误差均值和均方误差小,所以BP神经网络训练采用1个隐含层13个节点数.同时检验网络训练是否存在过拟合现象,以保障网络模型的泛化能力.通过网络训练检验可知,该网络训练不存在过拟合现象.

表 3 不同隐含层下不同节点数网络训练误差均值、均方误差Tab.3 Mean error and mean square error of network training with different hidden layers and numbers of nodes
如图2所示,神经网络训练样本达到21组时,训练误差为0.197 × 10-3,11次训练误差均值为2.13 ×10-3,均方误差为 6.091 × 10-6,达到理想的精度.
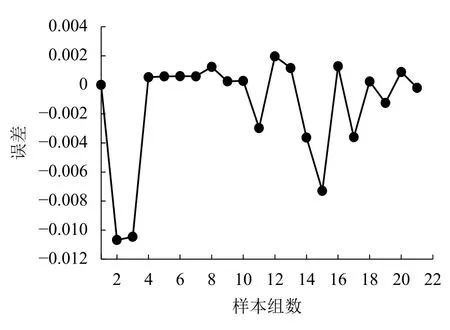
图 2 网络训练误差Fig.2 Network training error
3.3 神经网络验证
通过训练的神经网络对两组验证样本进行验证,见表4,一等座/二等座验证输出值跟实际评分的绝对误差相对较小,为-0.167/-0.072,相对误差百分比也较小,一等座为3.07%,二等座为1.42%.鉴于此,认为构建并训练的神经网络有效,并通过对比回归分析误差发现该预测精度较高.
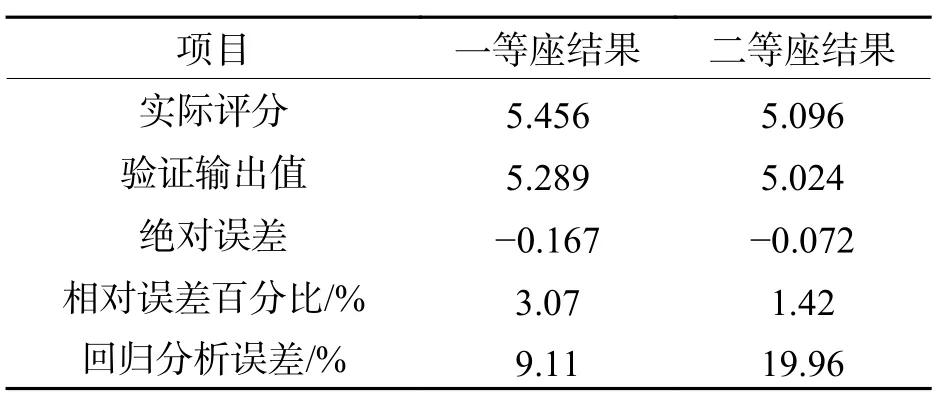
表 4 BP神经网络验证结果Tab.4 Verification results of BP neural network
3.4 神经网络数学公式表达
网络中输出层传递函数选用purelin,因此σ(n)=purelin(n)=n;

将式(5)、(6)和上述相关参数代入Mathematica等数学运算软件构建座椅静态舒适度评分的数学公式,通过输入座椅变量xi,直接得到座椅静态舒适度评分的输出值y,从而完成高速列车座椅人机几何参数测量数据输入到座椅静态舒适度评分输出的神经网络预测评价过程.
4 结 论
(1)提出了神经网络预测高速列车座椅舒适度的方法,该方法可以通过对座椅人机几何参数测量数据的输入直接得到舒适度评价输出,避免进行大量的问卷调查和统计分析,节省时间和成本.
(2)通过实例研究,构建了通过高速列车座椅人机几何参数测量数据来预测高速列车座椅舒适度的神经网络模型,并用CHR2一、二等座座椅样本验证了该神经网络对高速列车座椅舒适度预测精度较高.
(3)通过权值、阈值的提取,将训练好的神经网络转化为可搭载于数学运算软件的数学表达公式.
后续研究将增加座椅指标作为网络输入,并且增加训练样本,进一步完善基于人机几何参数的座椅舒适度评价模型.进而研究曲面参数跟主观舒适度的关系,构建完整的座椅舒适度模型.
