成层结构性软土一维非线性固结半解析分析

夏长青，胡安峰，付 鹏，崔 军，谢康和，周禹杉

（1.浙江大学滨海和城市岩土工程研究中心，浙江 杭州 310058；2.浙江大学软弱土与环境土工教育部重点实验室，浙江 杭州 310058）

结构性是天然软土的重要特征之一，形成的原因主要是土颗粒的排列方式、胶结作用、触变硬化等[1-2].结构性软土在被压缩时，会发生明显的结构屈服现象，软土地区的工程设计往往基于扰动或重塑土样所得到的参数进行计算，这将会低估土体在发生结构屈服前抵抗变形的能力，造成一定程度的经济浪费.若仅认识到在较低应力状态下其所呈现的低压缩性特点而忽视土体在结构破坏后的高压缩性，将会产生巨大的安全隐患.因此，在软土地基处理工程中，土体结构性是不可忽视的重要因素之一.

结构性软土的固结问题已经得到了国内外学者的广泛关注.沈珠江[3]认为原状土向重塑土转化的过程中土体变形模量应不断变化.王军等[4]采用分段式固结系数与渗透系数表征结构破坏前后土体性质的变化，但其推导得到的固结解析解仍属于线性固结理论范畴.Xie等[5-6]和Hu等[7]基于线性固结理论，考虑了软土的结构性与成层性，推导得到了近似解.曹宇春等[8]和刘洋等[9]采用有限差分法分别对结构性软土两折线模型和双对数非线性模型进行了求解分析.Karim等[10]将结构性土的粘弹塑性本构模型用于有限元计算中，以此预测路堤基础的长期沉降.Ozelim等[11]假设结构性土体为一维套筒式双弹簧固结模型，并利用结构破坏系数对破坏前后渗透系数变化作出了新的解释.

此前对于结构性地基的研究都不能同时考虑实际工程中地基的成层性和固结非线性的特征，而且大都采用有限差分法进行求解，求解过程冗繁且不够精确.因此本文综合考虑固结过程中软土的渗透性与压缩性的非线性变化以及不同深度处自重应力和结构屈服应力的变化规律，采用结构性土三折线压缩模型建立变荷载作用下的成层地基一维固结控制方程，采用半解析的方法进行求解分析，最后讨论了荷载变化、结构性等因素对固结性状的影响.

1 问题描述和模型建立

1.1 问题描述

采用如图1所示的成层饱和均质软土地基模型，根据底面是否透水分为单面排水和双面排水两种工况.荷载q(t)由q0开始逐渐增加，历时tc后达到最终荷载qu.其中若q0=qu，则为瞬时加荷；若q0=0，并保持加荷速率不变，则为线性加荷.其余假设同太沙基一维固结理论.

图 1 成层结构性软土地基模型Fig.1 Model of multi-layered structured soft soil foundation

1.2 模型建立

大量的室内压缩试验表明[12]，在e-lgσ′ 坐标下e为孔隙比；σ′ 为有效应力，结构性较强的原状土，其圧缩曲线常常表现为3段.当有效应力未达到结构屈服应力时，土体压缩性较小，将发生部分结构损伤的弹性变形；当有效应力增大至结构屈服应力后，土体结构开始发生破坏，压缩性急剧增大；最后土体结构被完全破坏，压缩性趋近于重塑土.据此建立结构性软土压缩模型如图2 所示.

图 2 三折线压缩模型Fig.2 Trilinear compression model

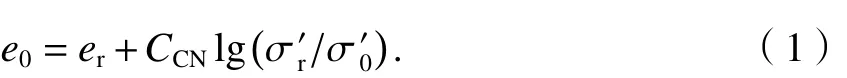
根据三折线模型，对成层地基任意第i层土，可得其孔隙比为

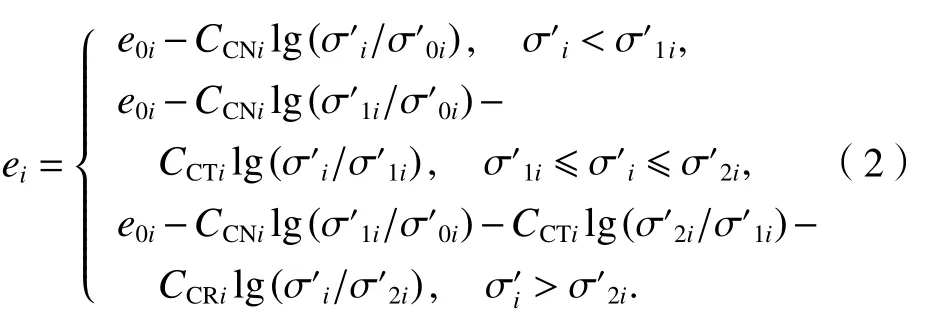
式中：i为原状土层的序号.

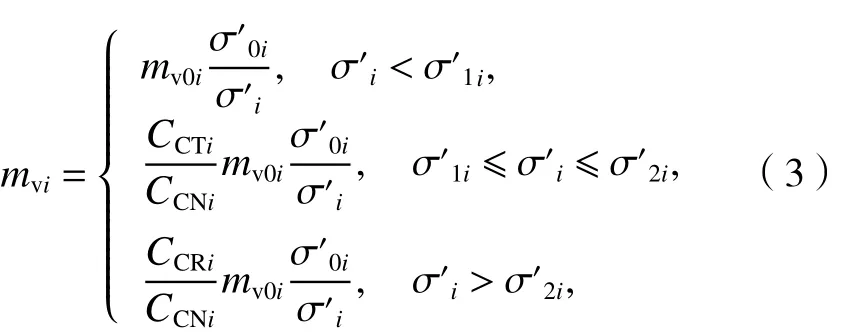
式中：mv0i为任意第i层的初始体积压缩系数，

如图3所示，当应变小于20%且初始孔隙比小于2.5，原状土孔隙比与渗透系数之间的关系可用elgkv模型描述[13]，其中：kv为渗透系数；kvr为参考点的渗透系数；kv0为初始渗透系数；Ck为渗透指数，e0-er=Ck（kv0-kvr）.Zeng 等[14]和 Horpibulsuk 等[15]都通过大量的渗透试验发现，无论是原状土还是重塑土，其孔隙比与渗透系数之间的关系是一致的，即与其所处的状态无关.

由此可推导得到三折线压缩模型第i层的渗透系数：

式中：kv0i为第i层土体初始渗透系数，Cki为第i层土体渗透指数.

试验表明，结构屈服应力的大小随地基深度的增大而增大[16]，其计算关系式如式（5）所示.该式与实测数据拟合较好.

式中：K1、K2为通过试验测得的常数.

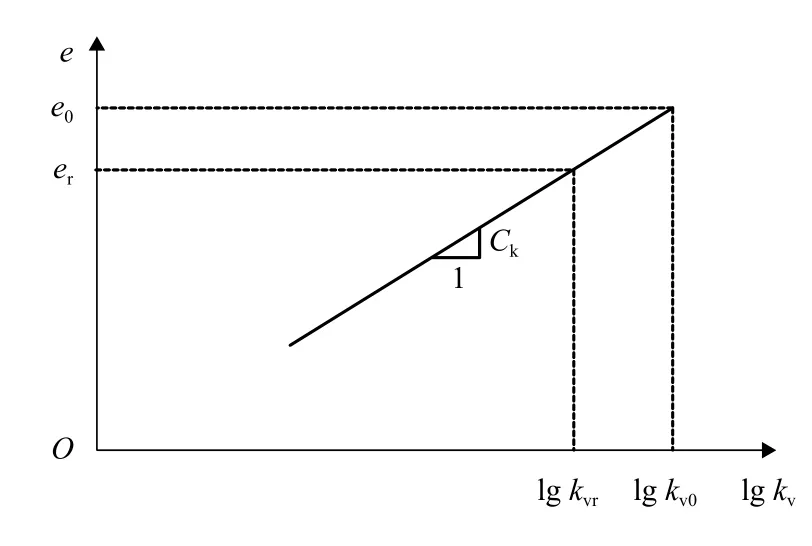
图 3 渗透模型Fig.3 Permeability model

1.3 固结过程描述

图4所示为单面排水固结的过程.随着荷载的增加，由于地基顶部超静孔隙水压力消散更快，结构屈服应力较小，有效应力将最先达到结构屈服应力，土体结构开始发生破坏.随着固结的进行，进入结构破坏阶段的土层逐渐增厚.当顶部有效应力增长至转折应力大小时，土体开始进入结构破坏后阶段，地基中将出现两条移动边界，从顶部向底部移动，若最终荷载较大，整个土体结构将完全发生破坏.

图 4 单面排水固结过程Fig.4 Consolidation process of single-drainage situation

图5所示为双面排水固结的过程，此时由于底部超静孔隙水压力消散更快，土体能更早进入结构破坏阶段，随着底部发生结构破坏的土层逐渐增厚，将形成一条向上移动的边界，而顶部土体与单面排水过程相同，形成另一条向下移动的边界.随着固结的进行，顶部和底部的有效应力先后达到转折应力，将形成两条移动边界并向中间移动，最终荷载较大时，土体将完全进入结构破坏后阶段.这种工况较单面排水更为复杂，本文将作主要研究，单面排水情况可以与此进行类比简化.

图 5 双面排水固结过程Fig.5 Consolidation process of double-drainage situation

2 问题求解与验证

2.1 解答

如图6所示，将厚度为H的成层地基离散为n层薄层，任一薄层厚度为hj，j为离散后薄层的序号，j=1,2,···,n，由于薄层厚度较小，同一薄层可认为参数相同，即体积压缩系数为mvj，渗透系数为kvj，薄层顶部和底部到地表距离分别为zj-1、zj.在离散过程中，移动边界同时也被划为某一薄层的边界.

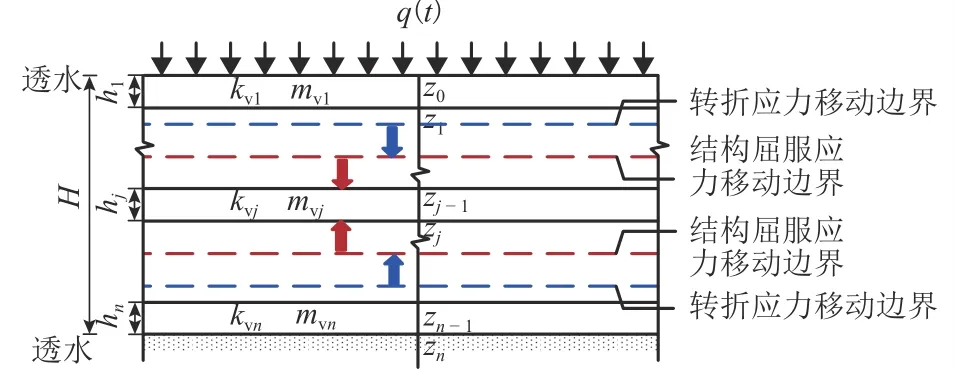
图 6 空间离散Fig.6 Schematic diagram of spatial discretization

同时将时间离散为微小的时间段，如图7所示，任一时间段k初始时刻为tk-1，终止时刻为tk.此时荷载也随之被离散，在时间段k内，荷载增量Δqk=qk-qk-1，由于时间微小，此时在该时间段内可看作瞬时加荷Δqk.

通过以上操作，在时间段k内，可利用成层地基线性固结解析解[17-18]进行求解.

图 7 时间和荷载离散Fig.7 Schematic diagram of temporal and loading discretization

则在时间段k内第j薄层的体积压缩系数和渗透系数为

则固结系数为

在时间段k内，控制方程为

式（7）、（8）中： γw为水的重度；cvjk为时段k第j薄层土的固结系数；ujk为时段k第j薄层土的超静孔隙水压力.

边界条件表达为

层间连续条件为

其中，j=1,2,3,···,n−1.

初始条件为

式中：

根据已有的成层地基一维线性固结解析解[18]，其解答为

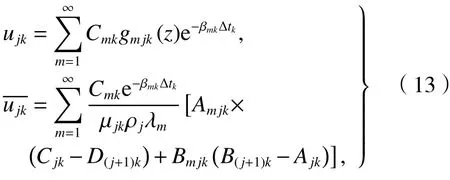
式(13)中：

λm为特征[方程]S(n+1)kSnk[S(n−1)k···S2kS1k=0 的正]T根，其中：

根据有效应力原理，有效应力为

则时间段k内第j层土按应力定义的平均固结度为

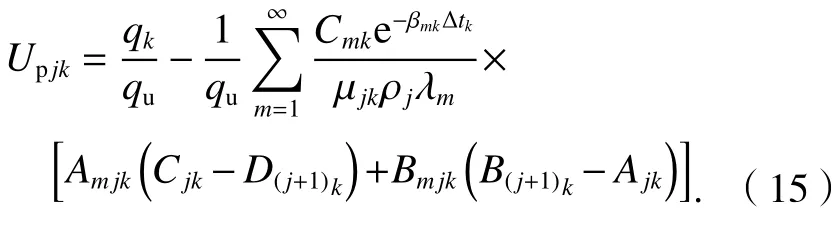
整个成层地基在时间段k内按应力定义的平均固结度为

时刻k第j层土压缩量为

于是在时刻k地表沉降为

地表最终沉降为

在时刻k按沉降定义的平均固结度为

2.2 验 证

为了验证该解法的可靠性，将编程计算得到的结果与成层地基一维非线性固结半解析解[19]进行对比，达到最终荷载时对应的时间因子Tvc= 0.032，最终荷载qu= 100 kPa，其它计算参数如表1所示.表中：Cc为压缩指数；γsat为土体饱和重度.由于取结构性土压缩时各阶段压缩指数相同，即结构性土虽发生结构破坏，但破坏前后土体性质没有发生变化，如图8所示.此时计算结果完全退化为不考虑结构性时的成层地基一维非线性固结解，证明了本文方法的可靠性.

表 1 对比验证计算参数Tab.1 Calculation parameters for verification

图 8 对比验证Fig.8 Verification by comparison

图 9 加荷速率对固结度影响Fig.9 Influence of the loading rate on the degree of consolidation

3 固结性状分析

以某4层具有较强结构性的饱和软土地基为例，双面排水，分析变荷载、结构性等因素对固结性状的影响，各层计算参数如表2所示.

表 2 4层地基计算参数Tab.2 Calculation parameters for four layered soils

3.1 变荷载对固结性状的影响

图9所示为加荷速率不同最终荷载相同情况下地基平均固结度的变化情况.可以看出，随着加荷速率的增大，超静孔隙水压力消散和沉降发展的速率均随之增大.由于考虑了结构性，当加荷速率相同时，在固结前期Up＞Us，而在固结后期Us＞Up.这是因为在固结前期，土体压缩性较小，所以沉降发展缓慢.

图 10（a）、（b）、（c）分别为最终荷载不同，但加荷速率相同时Us、地表沉降和Up的变化情况，图中，Tv为时间因子.由于最终荷载大小不同，导致土体结构最终破坏的程度也不同，如本例中qu=50 kPa时，结构未发生破坏，qu=1 40 kPa及以上时结构完全发生破坏.图10（a）中：固结前期，最终荷载越小Us越大；固结后期，最终荷载越小Us则越小.当最终荷载较小时，结构未发生破坏，此时沉降发展的速率始终较大，但压缩性较小，导致最终地表沉降量也较小（图 10（b））.图 10（c）中：Up的变化与图10（a）中Us的变化相似，Up随着最终荷载的增大而减小；在固结后期，最终荷载增大，Up也随之增大.

3.2 结构性对固结性状的影响

在进行结构性对固结性状影响的分析时，取最终荷载qu= 200 kPa，瞬时施加，与不考虑结构性的非线性固结理论进行对比，其中不考虑结构性时，压缩指数取结构破坏后阶段的值，其他计算参数如表1所示.

图11（a）为结构性对固结度变化的影响情况.可以看出，结构性对Us的变化影响较小，而考虑结构性会导致在固结前期Up显著增大，后期两者差值逐渐减小.这是由于结构性土固结前期压缩性小，孔隙较大，超静孔隙水压力消散的更快，后期两者压缩性接近，超静孔隙水压力消散速率也接近.图11（b）为结构性对地表沉降变化的影响情况.考虑结构性时，计算得到的沉降始终较小，原因仍与固结前期结构性土压缩性较小有关.图11（c）所示为结构性对土体超静孔隙水压力分布的影响情况，从中可以看出，考虑结构性时，超静孔隙水压力始终较小，孔压消散更快.

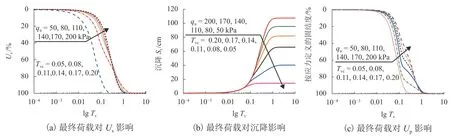
图 10 最终荷载对固结性状影响Fig.10 Influence of the ultimate load on the consolidation behavior

图 11 土体结构性对固结性状影响Fig.11 Influence of structural properties on the consolidation behavior

4 结 论

本文基于半解析的方法对结构性软土成层地基一维非线性固结问题进行了求解，其可靠性通过与已有理论对比获得证明，最后分析了变荷载和结构性对固结性状的影响，研究结论如下：

（1）最终荷载相同加荷速率不同时，考虑结构性的软土地基中超静孔隙水压力消散和沉降发展的速率均随加荷速率的增大而增大；在相同加荷速率下，固结前期Up＞Us，而固结后期Us＞Up.

（2）加荷速率相同最终荷载不同时，按沉降定义和按应力定义的平均固结度在固结前期均随着最终荷载的增大而减小，而在固结后期，变化情况相反.

（3）虑结构性会导致在固结前期Up值显著增大，后期与不考虑结构性的计算值相比两者差值逐渐减小，而Us值始终较为接近.此外考虑结构性所计算得到的沉降值始终较小.