横向偏位对截面不对称槽形PC梁受力的影响
2019-12-16朱利明邢世玲
朱利明 ,唐 俊 ,邢世玲
(南京工业大学交通运输工程学院,江苏 南京 210009)
预应力连续梁顶推法施工是通过水平液压千斤顶施力,借助滑道、滑块实现梁体升起、前移、下落、滑块退回4个步骤使梁体到位的方法[1],具有对桥下交通干扰小的优点,在跨越铁路线的桥梁中被广泛使用[2].在顶推过程中,由于多点顶推水平千斤顶出力不均匀和不同步等原因[3],混凝土梁的实际中线与理论中线会有横向偏差[4],现行《公路桥涵施工技术规范》对顶推过程中桥墩轴线与桥梁轴线的相对横向偏位规定值或允许值仅为10 mm[5],多点顶推的纠偏工序耗时较长,过小的限位阈值直接导致纠偏频率的增加,大大延长施工时间,增加施工成本.国内顶推施工均对《铁路桥涵施工规范》有关条例做适当修改,文献[6]根据计算将纠偏阈值定为50 mm;文献[7]依托实测数据发现主梁最大偏位可达到25 cm;文献[8]依托工程“昆明市南连接线高速公路工程五标段连续梁桥”,现场测得每个循环结束后梁体的横向偏位,将纠偏阈值定为50 mm.
相比对称梁截面,不对称开口截面对步履式顶推液压与电气控制同步性精度要求更高,梁体偏位会进一步影响液压同步性[9],形成恶性循环,增加桥梁顶推施工的安全隐患[10].因此,本文以天津第二大街跨津山铁路立交工程为背景,建立有限元模型研究横向偏位对不对称截面槽形梁变形和受力的影响.
1 工程背景
天津第二大街跨铁路桥主桥上部采用3跨(27 +27 + 38)m 预应力混凝土连续槽形梁,左右两幅,梁高4 m.单幅梁体宽16.6 m,梁底板净宽11 m,外侧悬臂板长3.0 m.槽形梁采用纵横向预应力体系,梁体前端安装25 m前导梁,后端安装13 m后导梁,采用步履式顶推施工横跨泰达站铁路线和津山铁路铁路线就位.浇筑0#~5#墩为永久墩,在铁路泰达站东侧铁路范围之外设置施工临时墩L1#~L10#,2#墩和3#墩之间设置L11#临时墩.开始顶推时,前导梁过L1#墩2.8 m;顶推48.8 m后梁体处于最大悬臂状态,此时前导梁和槽形梁前端共悬臂38 m,4#墩墩顶截面为4#墩支点截面,最大悬臂处槽形梁总体布置及4#墩支点截面如图1所示;顶推就位后,前导梁前端位于0#墩上,整个顶推施工梁体共前进127.8 m.

图 1 最大悬臂处桥型布置及4#墩支点截面图(单位:cm)Fig.1 Bridge arrangement at the maximum cantilever and the fulcrum section of the No.4 pie (unit:cm)
2 有限元数值模拟
采用通用有限元软件ANSYS模拟槽形梁在顶推过程中发生横向偏移时的受力情况.模型全长130 m,包括前导梁25 m,主梁92 m,后导梁13 m.由于横截面为不对称槽形截面,采用杆系单元难以准确反映其受力情况,故采用实体单元SOLID65来模拟混凝土槽形梁,导梁采用板单元SHELL63模拟,导梁间横向联系用梁单元BEAM189模拟,预应力钢束采用杆单元LINK8模拟[11-12].相关材料参数取值如表1所示.
利用参数数组、循环等命令建立几何模型,并进行网格划分.有限元模型网格划分与计算精度和效率密切相关,因此采用六面体扫掠划分.预应力的施加采用实体力筋法,力筋单元和实体单元用耦合自由度节点的方法联系,预应力的施加采用初应变的方式实现.梁体偏位通过滑道与槽形梁的相对移动来模拟,具体实现时采用槽形梁固定不动,通过滑道的移动来实现二者的相对移动[13].有限元模型如图2所示.

表 1 结构材料参数Tab.1 Parameters of structural materials

图 2 ANSYS有限元模型Fig.2 ANSYS finite element model
3 横向偏位对槽形梁受力和变形的影响
3.1 梁体未偏移时受力状态
选取最大悬臂状态(前导梁前端刚好未达到3#墩)为最不利状态[14],最不利截面为4#墩支点截面.为方便描述梁体的位移和应力,定义路径如图3所示:横截面行车道板上缘记为路径1,横截面行车道板下缘记为路径2,通过路径1和路径2来描述4#墩支点截面横向受力情况;选取左边梁下缘与左滑道接触处为路径3,右边梁下缘与右滑道接触处为路径4,通过路径3和路径4描述梁体纵向挠度变化规律.图中横截面以行车道板中点为桥中心线,向右为横向正方向,向上为竖向正方向,反向为负.
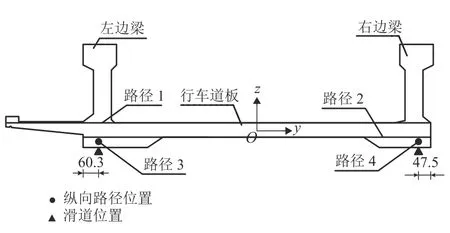
图 3 路径布置示意(单位:cm)Fig.3 Layout of route arrangement (unit:cm)
在自重和预应力荷载作用下,各个桥墩左右侧支反力如图4所示.

图 4 桥墩支反力Fig.4 Bridge pier support force
由图4可知,槽形梁横向截面不对称且滑道位置未能按重心对称方式设置,使得梁体左右受力不均衡,有人行道悬臂侧支座承受更大的梁体重量,梁体侧偏.梁体未偏移时,位移和应力如图5所示,截面应力受拉为正.
由图5可以看出:由于槽形梁横截面不对称,行车道板横向应力分布不对称,人行道上缘出现拉应力,主梁与行车道板结合处有应力较集中;行车道板左侧上缘应力为-2.47 MPa,右侧上缘应力为-1.91 MPa,右侧上缘应力较左侧小22.8%;行车道板左侧下缘应力为-6.91 MPa,右侧下缘应力为-8.68 MPa,右侧下缘应力较左侧应力大25.6%.
槽形梁左右边梁竖向和横向挠度变形不一致,竖向挠度和横向挠度最大处位于导梁前端.右边梁最大竖向变形挠度为111.58 mm,左边梁为106.32 mm,右边梁最大竖向变形较左边梁大5.26 mm;右边梁最大横向变形为5.29 mm,左边梁为5.00 mm,右边梁最大横向变形较左边梁大0.29 mm,梁体截面发生了横向畸变.
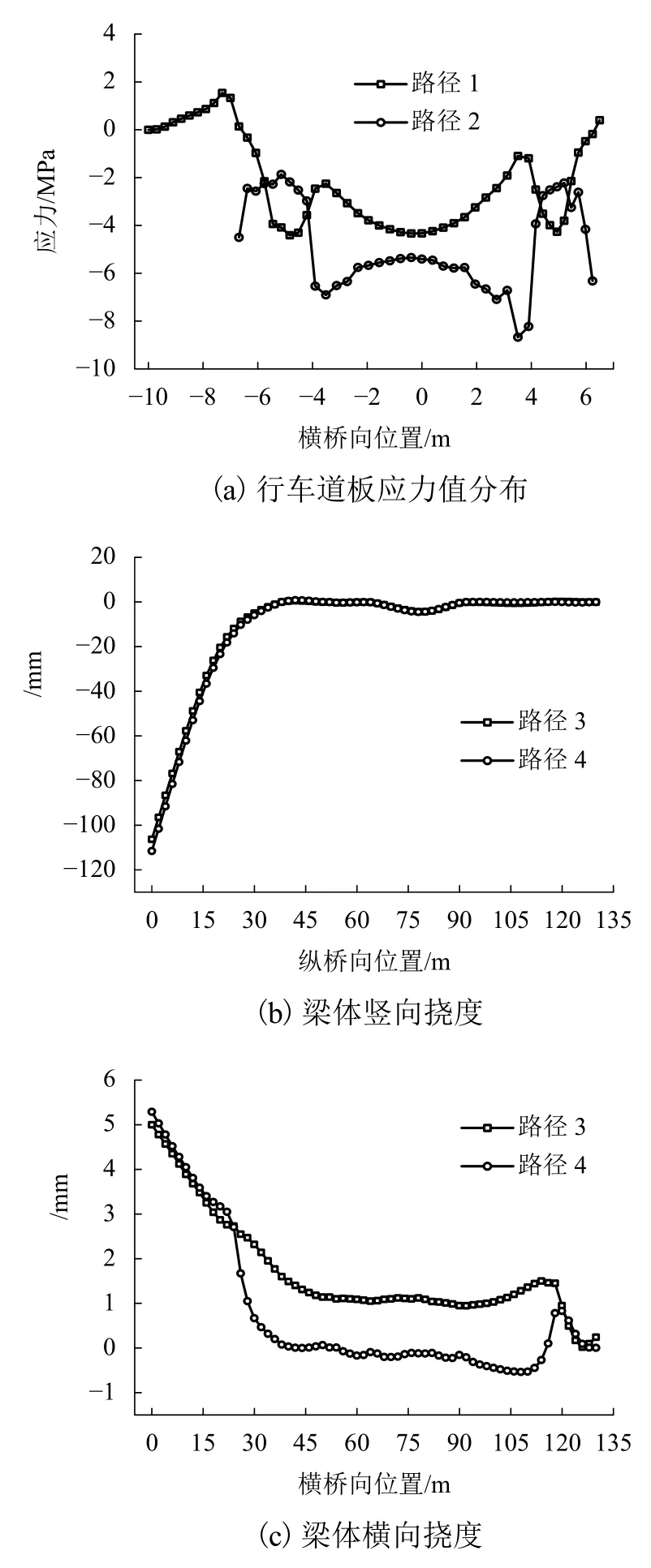
图 5 正常状况下梁体受力状态Fig.5 Force state of the beam in normal conditions
3.2 横向偏位方式的影响
多点顶推时需满足顶推力大于摩擦力和桥梁纵坡坡率之和的情况,梁体才能移动,即
自控逆变器输出电压在电机本体的定子绕组中产生电流,三相电流合成的电枢磁动势是按六步跳跃式步进转动的。例如,SaSbSc=(1 0 0) 表明A桥臂的上边导通,B、C桥臂的下边导通,此开关状态下电枢磁动势空间矢量F应转到A相轴正方向上。若将此开关状态下电枢磁动势空间矢量所对应的逆变器输出电压用u1(1 0 0)表示(下标1代表第1种状态),那末,与8种开关状态对应的逆变器输出电压ui(SaSbSc),下标i=0,1,2,…7,统称为电压空间矢量。
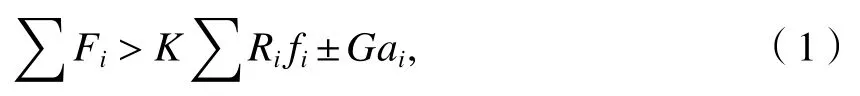
式中:K为安全系数,K取1.5~2.0;Fi为第i个桥墩千斤顶所施加的力;Ri为第i个桥墩滑道的瞬时支反力;fi为各支点相应的摩擦系数;G为梁体总重量;ai为桥梁纵坡坡率,上坡时顶推为“+”,下坡时顶推为“-”.
由图4可知,各桥墩左右支座支反力不同,而同一支座处的桥梁纵坡坡率是相同的.由式(1)可知同一桥墩左右侧的顶推力不同.而顶推力的不同加剧梁体受力的不均衡,会使得梁体在顶推过程中有横向偏位,造成梁体结构受力不平衡和落梁问题,施工过程中必须严格控制横向偏移量.
本文顶推装置的竖向千斤顶采用QF630-80型液压千斤顶,高度32 cm,外径35 cm.导梁前端下部宽40 cm,当最大悬臂工况下横向位移超过175 mm时,循环顶推之后导梁重心在千斤顶平面之外,落梁不稳,无法继续进行顶推施工.梁体偏位的方式主要有平动偏位和以不同桥墩为旋转中心的旋转偏位,如图6所示(以向右偏位为例).根据安全施工要求,限制导梁前端的最大偏移量D2,当以L2#及其左侧桥墩为旋转中心时,L6#墩处横向偏位D3大于4#墩处偏位距离D1,不符合以小偏位距离为限位装置安装距离的要求,故当梁体以L3#墩为旋转中心发生横向偏位时,4#墩支点截面有最大可偏移量D1.
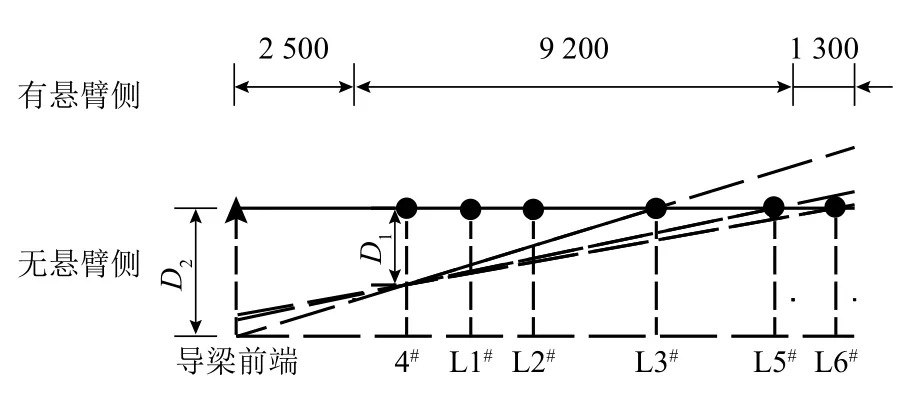
图 6 同侧梁体偏位方式(单位:cm)Fig.6 Schematic diagram of deflection of beam body at the same side (unit:cm)
满足施工要求的导梁前端最大横向偏位距离为175 mm,而由图5可知,在梁体未偏位时导梁前端已有5.29 mm的横向挠度,故拟定最大悬臂状态时旋转偏位导梁前端D2值为165 mm,此时对应4#墩支点截面横向偏位值D1为96 mm.为了获取最不利偏移方式,以图7所示4#墩支点截面为控制截面,研究4#墩支点截面偏位距离D1= 96 mm时,不同偏位方式对梁体受力的影响,具体工况如表2所示.

图 7 两侧梁体偏位方式(单位:cm)Fig.7 Schematic diagram of deflection of beam body on both sides (unit:cm)

表 2 横向偏位工况Tab.2 Transverse deflection conditions
在自重和预应力荷载作用下,各工况梁体发生偏移后的应力和挠度变化如图8所示.

图 8 不同偏位方式引起梁体受力差值Fig.8 Force difference between beams caused by different deflection modes
表3为各工况下4#墩支点截面行车道板左侧和右侧应力对比情况.表4为各工况下边梁变形挠度情况.
分析图8及表3、4可以看出:
(2)同一偏位方向不同偏位方式引起的竖向挠度增值基本相同,而不同偏位方向对其影响有所差别.以不同方向偏位时左右侧导梁前端竖向挠度差值不一致,梁体向右偏转时左右导梁前端竖向挠度差值约为5.3 mm,梁体向左偏转时差值约为5.2 mm.

表 3 行车道板左右侧应力对比Tab.3 Stress comparison between two sides of carriageway slab

表 4 导梁前端挠度值对比Tab.4 Comparison of vertical deflection values in front of guide beams mm
(3)相较旋转偏位,平动偏位引起的梁体横向挠度变化值幅度较大,平动左偏时距槽形梁梁体前端55 m处横向偏位挠度变化值为0.06 mm,而旋转左偏时为0.02 mm.
(4)4#墩支点截面横向偏位96 mm时,偏位方式引起的梁体受力变化值较小,导梁前端横向偏位均在满足安全落梁的施工要求范围内.
3.3 两点限位装置的力学参数
由图8及表3、4的分析可以得出,在满足安全落梁的施工要求条件下,整体横向向右平动偏位96 mm是梁体受力最不利偏位工况,且以最不利工况偏位引起的梁体受力变化值较小,结构安全,则顶推施工过程最大可偏位距离为96 mm.梁体发生最大偏位距离时,各支墩水平限位力如图9所示.
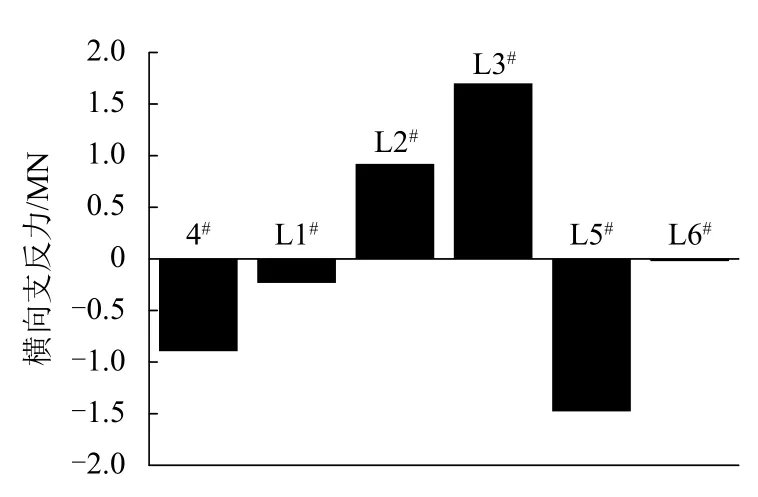
图 9 横向支反力Fig.9 Lateral reaction force
顶推过程中需要在安装顶推装置的支墩上设置侧制导架限位装,其包括3个组成部分:箱形钢结构的侧制导架底座、箱形钢结构的侧制导架立柱以及立柱上焊接的侧制导架限位板,限位板上可设置高阻尼块.由于两点限位平面上为静定结构,根据胡克定律:

式中:k为常数,是物体的刚度系数;xi为第i个桥墩横向偏位距离;Ni为第i个桥墩水平限位力.
由图9可知,最大横向限位力为1.7 × 106N,最大横向偏位96 mm,则阻尼块的最小刚度系数为18 ×103N/mm.
4 结 论
本文以世界首例顶推施工的不对称截面槽形梁为背景,建立有限元模型,研究了梁体横向偏位对截面不对称槽形PC梁受力变形的影响,得出以下结论:
(1)由于截面不对称且滑道位置未能按重心对称的方式设置,故槽形梁出现同一桥墩处左右侧支反力不等、两侧腹板整体竖向挠度不一致的问题,且若人行道不不布置横向预应力,则会出现横向拉应力,产生裂缝,故需将横向配筋延伸至人行道.
(2)针对单侧悬挑人行道的不对称截面形式,滑道安装位置偏向了悬臂侧,故未偏位情况下,无悬臂侧腹板相对有悬臂侧受力和变形都偏大.据此,以满足安全落梁的最大横向偏位距离为限值,梁体向无悬臂侧平动偏位是最能加剧横截面受力变形的不对称的方式,为最不利偏位方式.
(3)对比梁体未偏位时受力状态,以满足安全落梁的最大横向偏位距离平动偏位后,梁体受力变化值较小,结构受力安全,则认为满足安全落梁的最大横向偏位距离即为梁体可偏位的最大距离,并可将横纠偏阈值可适当放宽至此值,并以此计算出阻尼块的刚度系数.
