超重车模型及多-单车道荷载效应

刘 浪，陈东军，任青阳

（1.重庆交通大学省部共建山区桥梁及隧道国家重点实验室，重庆 400074；2.重庆交通大学土木工程学院，重庆400074；3.中建新疆建工路桥工程有限公司，新疆 乌鲁木齐 830002）

近年来，日常交通中大量涌现的工业重车，特别是当中的超重超载车辆，给现有公路桥梁带来极大的安全隐患，甚至导致桥梁结构开裂破坏和倒塌.例如，我国在2000年—2012年间由于超重车通行导致的桥梁倒塌事故就有17起[1].无独有偶，类似的桥梁倒塌事故同样发生在美国和哥伦比亚等国家[2-3].超重车属于特殊类别车辆[4]，产生的荷载效应远高于桥梁设计规范规定值，且其荷载特性与普通车辆存在显著差异，因此对这类车开展专项研究十分重要且必要.

不少学者曾通过数值模拟或现场荷载试验的方法对超重车进行研究[5-6]，由于当时缺乏先进的数据采集技术，早期的研究中鲜见超重车荷载特性及分布特征等内容.随后，因动态称重系统的广泛应用，又出现了大量与超重车相关的研究，并通过概率分析和可靠度理论与桥梁安全评估相结合[7-10].在以往的研究中，超重车均以车辆总重为判别标准，然而根据作者的前期研究，总重是影响车辆荷载效应的重要因素而非决定因素，如果车辆荷载空间分布合理，即便是重载，也不至引起过大的结构应力和变形[11].

为了更好地了解超重车荷载特性和代表性参数概率分布，特别是多车道多辆超重车并行时，给桥梁结构造成的荷载效应，本文收集了来自美国加州历时3 a的（weight-in-motion，WIM）数据，以加州许可荷载车模型为参照提取实测超重车数据，对典型超重车进行了特性分析，并分别对多车道和单车道超重车纵横向行驶情况开展研究.

1 超重车定义

目前，各国的超重规定不一.除美国外基本都以车辆总重或轴重不超过某上限值为标准.这样规定的优点是简单方便，适用于车辆过站例行检查.但在进行车辆荷载特性及桥梁结构反应分析时，宜考虑车辆荷载构成和分布对桥梁结构的影响.研究表明，总重是影响桥梁结构安全的重要因素但非决定因素，如果车辆荷载空间分布合理，即便总重较大也不至引起过大的应力和变形，可以安全通行[12].据此，美国国家公路与运输协会（American Association of State Highway and Transportation Officials，AASHTO）和各州交通厅分别制定了超重标准.例如加州交通厅根据州内重工业发展情况，制定了州许可荷载（permit truck）标准[13]，给出了相应的车辆模型如图1所示，模型由5辆不同轴数卡车组成，即5、7、9、11、13轴车各一辆，每辆车的轴间距均为5.5 m，除第一个轴重为115.6 kN外，其余轴重均为213.5 kN.对不同跨长，选产生最大荷载效应者作为标准.可见，加州超重模型的核心要义是“产生最不利效应”.鉴于文中所收集WIM数据来自美国加州I-50公路桥梁站点096，以及切合车辆荷载空间分布的研究目的，本文将以加州许可车辆模型为超重标准.

图 1 加州许可荷载模型Fig.1 Permit truck model issued by Caltrans

2 超重车荷载特性分析

本文通过美国加州交通厅收集了加州I-50公路桥梁096站点历时3 a的WIM数据，站点位处交通要道，为双向8车道.考虑同向行驶情况，4车道共记录了7 378 224辆车，以年为单位，对原始数据进行预处理，剔除其中存在问题的记录后共有6 311 122辆有效车辆数据，详尽的数据处理规则及方法可参考文献[11].首先分别计算出加州超重模型和实测 WIM车辆在规定跨长内（10、20、30、···、100 m）产生的最不利荷载效应，将相同跨长内荷载效应较加州超重模型大的车辆逐一提取出来，作为实测超重车WIM数据.下面对最终获得的近2 000辆超重车进行荷载特性分析.限于篇幅，文中图2仅列出2011年所记录超重车特性分析直方图.图 2（a）～（d）依次为超重车总重（gross vehichle weight，GVW）、轴重（axle load，AL）、轴距（axle distance，AD）和车辆行驶速度（speed，SPD）分布情况.从图中可以看出，4个超重车特性参数均呈现单峰值分布，其中总重主要集中在500～550 kN，轴重集中于80～90 kN，轴距集中于2～3 m，行驶速度主要在90 km/h.总体上看，通行频率最高的车辆为2轴和5轴车，其次是3轴和4轴车，2轴车虽然出现频率最高，但几乎没有超重现象，5～10轴车超重较为明显，以5轴车超重最为突出，其重量主要集中在350～400 kN，说明多轴长货车超重较为突出.图2（a）充分说明按照加州超重模型提取的超重车并非总重起主导作用，而是体现在重量的分布上，即总体呈现单个轴重大而轴距较小的分布情况.从年超重率来看，该站点超重车通行较多，最大超重率约为12%.

图 2 超重车荷载特性Fig.2 Characteristics of overloaded trucks

3 超重车模型分析

本文所收集的WIM数据按照车轴数来分，可分为从2轴车到11轴车共10种类型，其中2轴和3轴车未出现超重现象，10轴和11轴仅有少量超重车出现，其中超重频率最高的为5轴车和9轴车.为进一步定量分析超重车辆荷载，现将轴重和轴距这两个重要参数视为随机变量，对提取的超重车进行参数统计分析，并绘制于表1中.由于10轴和11轴车样本数量过小，故仅列出4～9轴车的情况.其中5轴超重车最多，占到所有超重车数量的38.2%，其次，7、4、9轴超重车相对较多，分别占19.1%、17.4%和14.9%，仅有少量6轴和8轴超重车出现.总体上，表中列出的6种超重车均表现为首个轴重相对较小而轴距较大，从轴距的计算结果可以看出绝大多数5轴、7轴、8轴和9轴超重车属于拖挂车，即采用3 + 2、5 + 2、5 + 3和5 +4的典型工业重车形式.下面对数量最多的5轴挂车进行轴重分布类型分析，图3为5轴车第1～5轴轴重的概率分布情况，分别记为AL5-1～AL5-5.其中2、5轴服从极值分布，其余3轴服从正态分布.统计轴重的均值μ和标准差σ如图3所示，单位：kN.

表 1 超重车模型及其特性参数统计Tab.1 Schematic overloaded truck models and their statistical parameters

图 3 5轴超重车轴重分布Fig.3 Distributions of axle loads of 5-axle overloaded trucks

4 超重车多-单车道荷载效应计算

4.1 多-单车道荷载效应定义

数据采集站点为同向4车道桥梁，必然存在多辆车并行的情况，即在两个垂直方向——同车道纵向及毗邻车道横向的并行.如果桥梁的计算跨径相对较长，那么此类并行现象会更为突出[14].作者曾在超重车辆荷载研究前期提出了基于马尔科夫链随机过程理论的多车道车辆荷载并行效应计算方法，考虑同跨内多辆车并行引起的叠加荷载效应，建立了相应的计算模型和公式，研究结果表明，随着桥梁计算跨径增大，多辆超重车并行概率增大，且造成的叠加荷载效应也显著增大[15].为进一步对比多车道与单车道荷载效应间的差异，现对多车道的叠加荷载效应和单车道荷载效应分别作如下定义：

式中：Li_total为第i个荷载工况（车队）引起的叠加效应，Li1、Li2、Li3和Li4分别为该荷载工况（车队）在1～4 车道引起的荷载效应；D1、D2、D3和D4为 4 条车道对应的分布系数[16-17]；Lj_onelane为单车道第j个荷载工况（车队）引起的荷载效应.

4.2 多-单车道荷载效应计算

首先建立车队研究单元，利用WIM数据记录的车辆行驶速度和到达时刻，计算出车辆间的车头距 = 到达时刻差 × 前后两辆车平均速度，再通过时序和行驶车道记录还原各辆车在桥面的分布位置，顺次将N辆车组合为一个车队，根据桥梁跨径计算长度不同，N可变.针对文中采集数据的桥梁情况，将N取为21，以保证在同一跨内并行的所有超重车均在车队之列.以第1～21辆车组建的第1个车队为例，选取中间第11辆车为主车，确定其距桥跨端部的距离，其余车辆则按照车头距依次排放于桥面.考虑多车道时，计算整个车队通过桥梁造成的叠加荷载效应；计算单车道时，仅考虑主车所在车道（主车道）纵向行驶车辆造成的荷载效应.由此，即完成了第1个荷载工况（车队）的加载.然后，将主车顺次后延一辆组成一个新的车队，按照同样的方式计算出相应的荷载效应.以此类推，计算出记录中不同车队造成的荷载效应，再通过排序获得其中的最不利荷载效应.

根据上述计算模型，本文自行编制了基于车队的多-单车道荷载效应影响线计算程序，建立了采集数据桥梁的模型.该桥梁为预应力混凝土简支梁桥，其横截面如图4所示，共设定10～100 m的11个常见中小单跨跨径，站点为同向4车道，故式（1）中主车道荷载分布系数为：主车道1.00，2车道0.45，3车道0.15，4车道0.05[16-17].程序依次读入提取的超重车WIM数据组建车队，并分别计算每个车队引起的多车道叠加荷载效应和相应的单车道荷载效应.

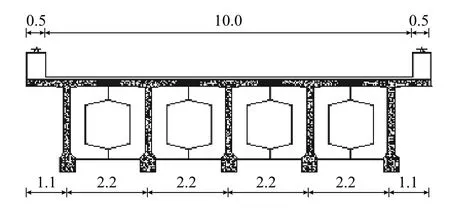
图 4 预应力混凝土梁桥横截面（单位：m）Fig.4 Cross-section of prestressed concrete girder bridge (unit：m)

4.3 多-单车道荷载效应与中美规范对比

现对11个跨径计算所得的多-单车道荷载效应排序，将其中的最不利跨中弯矩和支座剪力与中美桥梁设计规范进行对比，其中中国按照《公路桥涵设计通用规范》 JTG D60—2015[18]公路-I级荷载（后简称JTG2015）计算，美国按照AASHTO Standard Specifications for Highway Bridge Design[19]HL-93汽车加车道均布荷载（后简称AASHTO）计算，结果如图5所示，图例中的数字表示数据年份，M表示多车道，S表示单车道.

图 5 多-单车道荷载效应与中美规范对比Fig.5 Comparison of load effects of multiple-one lane and values specified in JTG and AASHTO

由图5可知，多车道叠加荷载效应较单车道以及中美规范值都大得多，而单车道荷载效应与规范值相近或略高一点.

表2中详尽列出了各跨长对应的多车道与单车道荷载效应之比，其中跨中弯矩最大比值为2.05倍，平均比值为1.65倍；剪力最大为2.05倍，平均为1.70倍.上述结果表明，超重车并行引起的叠加荷载效应较为显著，其计算值远大于现行中美规范值，对于有重型车辆频繁通行的多车道桥梁设计和评估，应考虑重车荷载特别是重车并行引起的叠加效应.

图6为WIM数据中所提取引起最不利荷载效应的超重车并行过桥实景，限于篇幅，下文仅列出了两个典型例子：图6（a）为两辆5轴车横向并行，两者车头间距为0，图6（b）为两辆9轴车横向并行，两车车头距亦为0.从轴距分布来看，4辆车均属拖挂车，采用3 + 2和5 + 4的工业车形式，其共同特点为拖挂部分轴重很大而轴距很小，车辆主体部分亦存在相似情况.

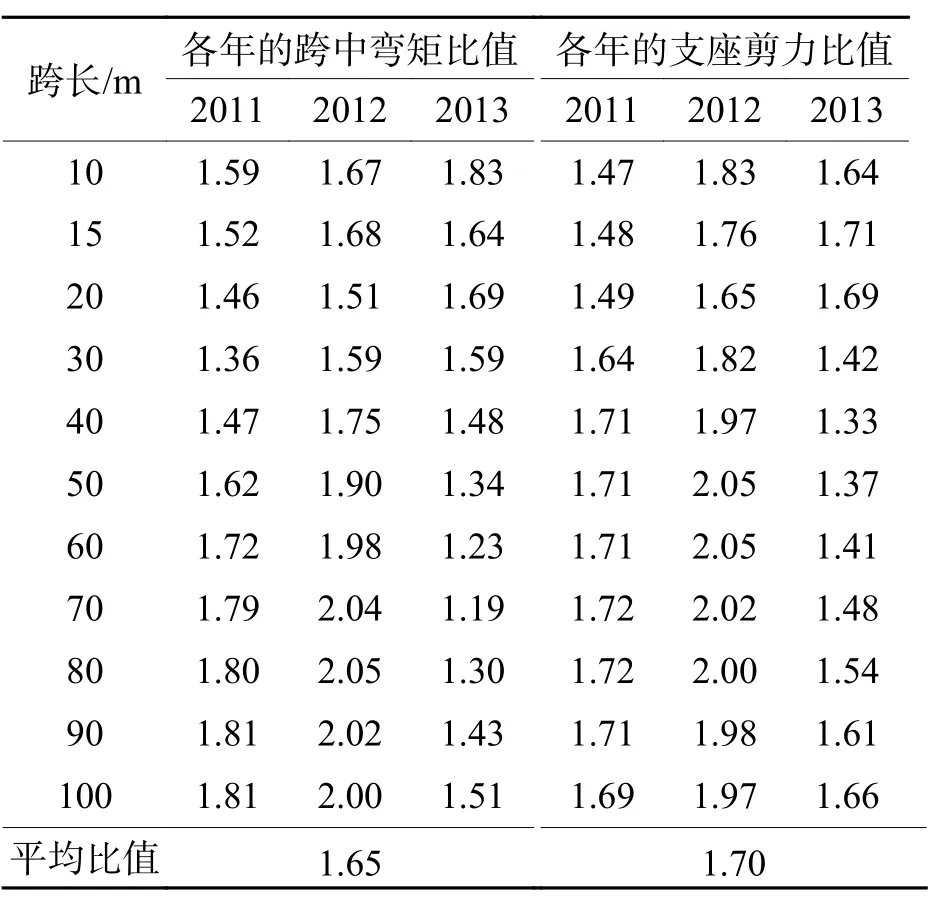
表 2 多-单车道荷载效之比Tab.2 Ratios of load effects of multiple lanes to one lane

图 6 典型超重车并行过桥实景Fig.6 Scenarios of multiple overloaded trucks moving on lanes

5 结 论

（1）超重车总重GVW、轴重AL、轴距AD和车辆行驶速度SPD均呈现单峰值分布，总重主要集中在500～550 kN之间，轴重集中于80～90 kN之间，轴距集中于2～3 m之间，行驶速度主要在90 km/h，总体呈现单个轴重大而轴距较小的分布情况.

（2）2轴和3轴车未出现超重现象，10轴和11轴仅有少量超重车出现，超重频率最高的为5轴车和9轴车.大多数5轴、7轴、8轴和9轴超重车属于拖挂车，5轴车轴重服从极值或正态分布.

（3）多-单车道荷载效应与中美规范的对比表明，多车道叠加荷载效应较单车道以及中美规范值都大得多，单车道荷载效应与规范值相近或略高一点.其中多-单车道跨中弯矩最大比值为2.05倍，平均比值为1.65倍；剪力最大为2.05倍，平均为1.70倍.

参考文献：

[1]FU Zhongqiu，JI Bohai，CHENG Miao，et al.Statistical analysis of the causes of bridge collapse in China[C]//Proceedings of Forensic Engineering:Gateway to a safer tomorrow.Reston：ASCE， 2012：75-83.

[2]DIAZ E E M， MORENO F N， MOHAMMADI J.Investigation of common causes of bridge collapse in Colombia[J].Practice Periodical on Structural Design and Construction， 2009， 14(4)： 194-200.

[3]孙莉，刘钊.2000～2008年美国桥梁倒塌案例分析与启示[J].世界桥梁，2009(3)： 46-49.

[4]MOSES F and GHOSN M.Calibration of a Bridge rating formula for overload permits[C]//ASCE Structures Congress， Bridges and Transmission Line Structure.[S.l.]： ASCE, 1987： 1245-1251.

[5]ZHANG Jianren， PENG Hui， CAI C S.Field study of overload behavior of an existing reinforced concrete bridge under simulated vehicle loads[J].Journal of Bridge Engineering， 2011， 16(2)： 226-237.

[6]VIGH A， KOLLAR L.Routing and permitting techniques of overweight vehicles[J].Journal of Bridge Engineering， 2007， 12(6)： 774-784.

[7]韩万水，闫君媛，武隽，等.基于长期监测的特重车交通荷载特性及动态过桥分析[J].中国公路学报，2014，27(2)： 54-61.HAN Wanshui， YAN Junyuan， WU Jun， et al.Extraheavy truck load features and bridge dynamic response based on long-term traffic monitoring record[J].China Journal of Highway and Transport， 2014， 27(2)： 54-61.

[8]HAN Wanshui，YUAN Yangguang，HUANG Pingming， et al.Dynamic impact of heavy traffic load on typical T-beam bridges based on WIM data[J].Journal of Performance of Construction Facilities，2017，31(3)： 1-14.

[9]HAN Wanshui， WU Jun ， CAI C S， et al.Characteristics and dynamic impact of overloaded extra heavy

trucks on typical highway bridges[J].Journal of Bridge Engineering， 2015， 20(2)： 1-11.

[10]李全旺，李春前，孙健康.基于结构可靠性理论的既有桥梁承载能力评估[J].工程力学，2010，27（增刊2）：142-151.LI Quanwang， LI Chunqian， SUN Jiankang.Reliability-based capacity assessment of existing bridges[J].Engineering Mechanics， 2010， 27 (S2)： 142-151.

[11]刘浪.基于WIM的公路桥梁车辆荷载特性分析[D].上海：同济大学，2014.

[12]ROGER D T.Overload truck wheel load distribution on bridge decks[R].Michigan：Michigan Department of Transportation， 2009.

[13]CALTRANS.California amendments to AASHTO LRFD bridge design specifications.4th Edition[S].California：California Department of Transportation，2008.

[14]尤吉.基于WIM卡车数据的公路桥梁承载力评估[D].上海：同济大学， 2009.

[15]刘浪，唐光武，刘海明.考虑多车道行车效应的车辆荷载外推方法研究[J].福州大学学报（自然科学版），2017，45(2)： 222-225.LIU Lang， TANG Guangwu， LIU Haiming.A study on extrapolation method for vehicle load on highway bridges with multiple lanes[J].Journal of Fuzhou University (Natural Science Edition)，2017，45(2)：222-225.

[16]FU G K， LIU L， BOWMAN M D.Multiple presence factor for truck load on highway bridges[J].Journal of Bridge Engineering， 2013， 18(3)： 240-249.

[17]AASHTO.LRFD bridge design specifications[S].5th ed.Washington D.C.： AASHTO， 2010.

[18]中华人民共和国交通运输部.公路桥涵设计通用规范：JTG D60—2015[S].北京：人民交通出版社，2015.

[19]AASHTO.Standard specifications for highway bridge design[S].17th ed.Washington D.C.： AASHO， 2002.