初中数学课堂教学“设问关键点”策略研究
2019-12-16浙江省杭州市余杭区临平第三中学余咏娟
浙江省杭州市余杭区临平第三中学 余咏娟
一、问题的提出
课堂提问是数学教学中互动反馈的有效手段,是启发式教学的有效形式,要把数学课上好、上出彩、上高效,不仅要有完整清晰的教学设计,还要有有效的问题设计与之相呼应。美国教学法专家斯特林·G·卡尔汉认为:“提问是教师促进学生思维、评价教学效果以及推动学生实现预期目标的基本控制手段。”如果在课堂中没有高效的数学问题,没有循序渐进的设问,课堂就会显得比较单薄,显得没那么有灵气;教师与学生的沟通会就会显得呆板,没那么生动;学生在课堂会也会学得比较机械,思维的深度会也会受到很大的影响。
有效的问题能使学生产生困惑,同时促使他们积极思考,从而发现新问题,并主动去解决新问题。所以,数学课堂教学应从问题开始,精心设计问题。在教学中要充分了解学生的数学知识能力水平,提出的问题要恰到好处,问题既不过分难,又不过分简单,提出问题的方式要引起学生的兴趣和好奇心,语言要有情趣,内容要有较丰富的直观背景,要不断引导学生多思、多问、多动手,促使学生的注意、记忆、思维高度凝聚,让他们在注意力最集中、思维最活跃的状态下进行尝试和创造性学习。因此,笔者认为课堂问题的设计必须遵循一定的策略。
二、数学课堂中问题设计有效性具体操作中的几点策略
1.课堂中设计有层次的问题,优化学生数学学习过程
问题的呈现应该有一定的层次,这样有利于学生对问题的认识和对知识的不断领悟,能激起学生思维的波澜涌动。这样的问题设计也符合维果斯基的“最近发展区理论”,该理论认为:学生的学习状态有两种水平,一种是目前已达到的水平,一种是潜在可能达到的水平,这两种水平之间的距离就是最近发展区。教学中,我们的问题设计应该符合这样的状态,不要把问题拔得比较高,这样不利于学生的学习,最好做到跳一跳能达到的状态,这就需要老师在课堂中设计不同层次的问题把难度分解。
例如:某商场将进价为2000 元的冰箱以2400 元售出,平均每天能售出8 台。为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施。调查表明,这种冰箱的售价每降低50 元,平均每天就能多售出4 台。如果你是市场调研员,你将建议冰箱销售价定为多少,使得商场获利4800 元?尽可能多?说明理由。
为帮助学生解决问题,我们将问题分解,并设计出4 个小问题,层层深入。
问题1:如何理解冰箱销售量与销售定价之间的关系?


问题2:如何理解商场每天销售冰箱获得利润与销售定价之间的关系?


于是发现,冰箱销售利润与销售定价之间满足二次函数的关系。任取三个点的坐标值,代入二次函数关系式,可求出两个解析式。
问题3:要使这种冰箱的销售利润平均每天达到4800 元,每台冰箱的定价应为多少元?


问题4:商场每天能获得5000 元的利润吗?5200 元呢?试用所学知识进行说明。
根据上面问题中的式子中,令y=5000,y=5200,看所得到的方程是否有解来说明,或者是利用二次函数的最大值来说明。
通过这样四个问题的分解,学生对这个习题有了系统的认识,进一步了解了方程与函数的关系。在求解的过程中解决了新问题,有利于突破二次函数在利润问题中的应用,把低层次的知识变为高层次的知识,如此循环往复,可以使学生把数学的思想方法应用于现实中去。
2.在关联点处设计深度的问题,新课一气呵成
在学习新的知识时,学生要把新授课中的关联点前后连接起来才能形成思路,但是学生往往在这些关联点处出现思维障碍,不易形成连贯的思维。教师若能在受阻关联点处设置合理的问题,引导学生由一个关联点迈向另一个关联点,新学的知识就会一气呵成。
例如:证明命题“三角形的三个内角的和等于180°”是真命题。

已 知: ∠A、 ∠B、 ∠C为△ABC的三个内角,求证:∠A+∠B+∠C=180°。
学生很快就找到方法,过A点作直线MN∥BC,很快就证得。
问题1:你怎么想到“过A点作直线MN∥BC”?
问题2:还有其他转移方法吗?
学生:作射线BD,过C点作CE∥AB,如上图,∵CE∥AB,∴ ∠1= ∠A, ∠2= ∠B, 而 ∠C+ ∠1+ ∠2=180 °,∴∠A+∠B+∠C=180°。
问题3:我们是否把顶点放在B处?我们可以通过作平行线把我们想要的角放在我们想要的位置,转化为一个平角。
问题4:这个平角是否可以放在BC边的任何位置呢?又该如何实现角度的转移?
问题5:你们还有其他的思路吗?本题解决问题的主要方法或数学思想是什么?
其实我们发现平角的顶点可以放在任何位置,它们共同的思路就是利用平行线的性质把三个角进行转移。本题的三个思维关联点是:(1)添加平行线;(2)平角顶点的任意性;(3)提炼转化思想。问题1 引导学生认识平行线是转化角的工具,初步体会转化思想的应用。问题2、3、4 以作平行线为手段,把平角的顶点放在C点,B点,BC边的任意位置,最后放在平面中的任意位置,到此,学生思维火花四射。
新课内容的关联点并不多,如能在关联点处精心设计问题,则可以起到画龙点睛的作用,让学生举一反三,对数学思想与方法做到心领神会,融会贯通。
3.在发散点处设计合理的问题,做到数学思想方法的统一
在数学课堂中,教师要准确把握问题的发散点,并在发散点设计合理的问题,这样可以达到以一当十的练习效果,有利于培养学生的发散性思维和创造性思维。通过对发散点的确立以及问题的追问,有利于学生对这类问题的深入了解,促使学生去归纳和整合,优化自己的知识结构。
例如:已知梯形的上底为8,下底为15,一腰长为6,则另一腰a的取值范围为__________。
分析:这个题目的难点是取值范围和作图,其实范围问题的核心还是腰a的值的几何刻画与代数刻画。我们很快发现,代数刻画按目前知识做不到,这样自然想几何刻画,那我们马上联想到几何长度的范围在三角形中有,这里自然就有几种画法了。
问题1:是否可以考虑作辅助线?
本题的发散点:在梯形中如何去作辅助线,然后找到合理的三角形和最基本的四边形(平行四边形,正方形、矩形)?
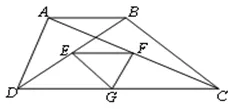
问题2:你们能否用这个添辅助线的方法解决下面这个问题:如图,梯形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点。已知梯形的两底差是6,两腰和是12,则△EFG的周长是______。
首先我们应该让学生聚焦在周长上,我们很快发现两条已经是中位线了,还有一条不是,那就要找三角形让它也变成中位线,那连接BF就可以,学生就非常清楚了,现在再来总结这条辅助线的特点,学生永远就不会忘了。
问 题3:在 梯 形ABCD中,AD∥BC, 对 角 线AC⊥BD, 若AC=12,BD=9,则梯形的面积为_______,中位线为______。

对于第一个问题,我觉得先应该引导学生思考梯形面积的求解的通法,学生会发现问题无法求解,这时老师可以适时引导学生进行转化。首先会想到割,因为对学生的思维来说这样比较容易思考。
问题4:两个三角形△ABC与△ADC的面积分别为多少?我们可设OD为a,那么通过代数的运算就解决了。
问题5:如果用补的思想,平移AC到D,梯形面积会变成什么?变成三角形面积,问题进一步简化。
在发散点设计有效问题,让学生在平面几何问题中通过这样的思考,会加深印象,进一步感受到割补法的魅力与转化思想的重要性,学生会自然而然地感受到里面的数学本质。
4.在拓展处设计合理的问题,加强知识梳理的能力
很多的数学问题中存在拓展点,教师可以对一个基本问题进行巧妙引导,把学生的思路引向问题的拓展点,并在拓展点处设问,挖掘思维的深度,这样学生思维的条理性和创造性得以培养。通过典型例题找准拓展点,进行适度的拓展预设,不断地就拓展点对学生进行追问,既有利于知识的梳理,又可以查漏补缺,达到拓展提升的目的。
问题1:做这题你的主要方法是什么?你有怎样的收获?
分析:这个问题以函数为背景,综合考查了四边形、方程、函数、分类讨论等相关知识与核心思想方法,能较好地考查学生综合运用解析几何的能力。然而反观原题,总给人一种意犹未尽之感。其实我们对这样的问题可以创新和开发出很多新的问题。
我们可以发现这些问题的两个拓展点:直线的形式发生改变,直线由定直线变成了动直线或是另外曲线;双曲线的形式发生改变。

(1)当点A的坐标为(4,2)时,点B的坐标;
(2)当yB=2yA,点H是BG的中点时,证明G是HC的中点,并求出双曲线的解析式。

(1)求抛物线的函数解析式;

(1)求b的值;
(2)求B的坐标;
(3)点P为抛物线上的一动点,当-2<x<4 时,求使得四边形AODP为菱形的点P坐标。
问题5:当曲线发生改变时,解决这类问题的数学思想方法发生改变吗?
通过这些问题的拓展,可以让学生感受到这类问题的本质,进一步掌握解析几何的共同点,从几何中找到合理的方程。同时,通过问题跟进式的探究学习,可以为课堂节省很多时间,同时也不减少课堂容量,使得探究不再是难事,进一步提高课堂效率。还可以让学生参与问题的编拟,让学生进行再次发现问题、提出问题及解决问题的探究尝试,理解这类问题的实质,从而进行“再创造”。
课堂问题的设计是一门教学艺术,有效问题的设计有利于学生数学概念的生成、理解,有利于学生对例题和习题的求解、归纳、延伸等,有利于数学思想方法的提炼。我们必须重视课堂问题的设计,最大限度地提升课堂教学的有效性。
