基于安装误差的导引头隔离度测量值修正
2019-12-14周永恒崔少辉
周永恒,崔少辉,方 丹
(陆军工程大学石家庄校区,河北 石家庄 050003)
0 引 言
红外成像导引头是引导导弹完成对目标的搜索、识别与跟踪的高精度传感器。但受发动机和空气阻力影响,导引头在制导过程中弹体始终处于剧烈抖动,从而导致导引头光轴发生偏移和摆动,甚至丢失目标[1-2]。因此,保持视轴稳定是导引头光电探测系统实现目标识别跟踪的基础,实现隔离度的准确测量对红外成像导引头性能的评估鉴定具有重要意义。
目前国内外对导引头隔离度测试方法研究较多,但对隔离度测量值误差的研究还比较少见。国外对导引头隔离度测试的研究主要集中于仿真测试实验室的建立,如美国20世纪70年代建立的“自动红外成像导引头性能评估实验室(AIISPES)”[3],该系统能够对包含隔离度在内的导引头主要性能参数的进行准确测量。到2007年,美国空军电子战评估中心(air force electronic warfare evaluation simulator,AFEWES)[4]已研发出拟真程度高、红外对抗模型齐全的红外导引头半实物仿真测试系统。与此同时,英国、荷兰、加拿大等国家的相关部门也建立了相关实验室来开展红外导引头的测试工作[5]。
国内主要集中于测试理论与测试方法的研究,朱华征等[6]、李富贵等[7]对平台导引头隔离度及隔离度寄生回路测试方法进行研究,提出了等效回路测试的方法,可获得较高的测试精度;但该方法仅适用于导引头伺服系统的开发阶段。孟令东[8]、张安峰[9]等基于光-电-机-算相结合的方法来实现对光电稳定系统稳定精度的测试,可为系统评价提供有力依据;但测试设备复杂,难度较大。目前红外导引头隔离度的主要测试方法是利用三轴转台来模拟弹体的扰动,使其按照一定的频率与幅值振动来进行隔离度的测试[10-11];该方法需将红外导引头安装于转台内框,不可避免地会引入安装误差,使得模拟弹目视线运动与理想弹目视线运动不重合产生附加误差,这些误差直接影响导引头隔离度的测量结果[12]。随着导引头精度的提升,对导引头隔离度的要求也越来越高,如不考虑安装误差影响所得测试结果无法满足测试精度要求。
本文基于多体建模理论建立了导引头安装误差模型,分析了由安装误差导致的导引头隔离度测量误差,并给出了隔离度测量误差的补偿方法。
1 导引头隔离度测试及其系统
隔离度是导引头的一个重要指标,表征导引头对弹体抖动的隔离能力。这里将隔离度 γ定义为红外导引头输出视线角速度与弹体转动角速度之比。
红外成像导引头半实物仿真测试系统主要包括五轴飞行转台、红外目标模拟器、视频分析仪及记录系统、总控与测评系统、实时数字接口、分布式通信系统,如图1所示。红外导引头安装于五轴转台的内框,导引头回转中心与转台回转中心重合,模拟导弹飞行过程中俯仰、偏航、滚转三个自由度的扰动;红外目标模拟器架设于外框,产生目标模拟信号,导引头接受目标辐射信号,并通过伺服系统控制导引头光轴始终指向目标;综合控制台用于仿真系统的控制、管理和集成,并实时采集转台和导引头输出视线角速度数据。
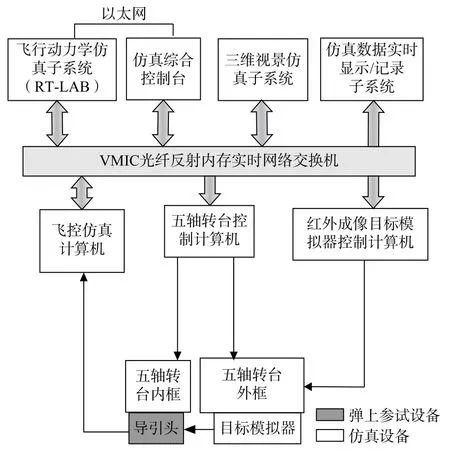
图1 导引头半实物仿真测试系统框图
隔离度测试原理如下:测试过程中,目标保持静止,导引头处于目标跟踪状态;给转台内三轴输入幅值为A,频率为弹体自振频率的正弦信号,模拟弹体飞行过程中的扰动;由于导引头隔离度的存在,导引头产生视线角速度输出,则隔离度计算公式为:
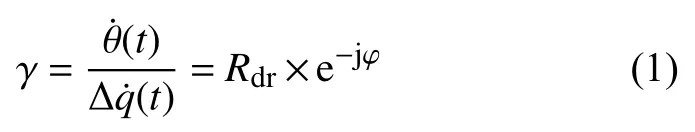
其中,Rdr反映了隔离度的幅值特性,φ反映了隔离度的相位特性。
2 导引头安装误差分析及建模
2.1 导引头安装误差分析
在五轴转台内三轴上建立转台基准坐标系(惯性坐标系)O-x0y0z0,转台安装基面坐标系O-x1y1z1,导引头体坐标系O-x2y2z2以及视轴坐标系O-x3y3z3。转台基准坐标系以转台回转中心为坐标原点O,Ox轴指向目标初始位置,Oy轴沿垂线向上,Oz轴与其他两轴垂直并遵循右手定则。
理想情况下,导引头体坐标系O-x0y0z0与转台安装基面坐标系O-x1y1z1应当完全重合。但由于安装误差的存在,实际导引头体坐标系与理想体坐标系坐标原点之间存在位置偏差,且对应的各个轴系间存在角度偏差。设红外目标模拟器到转台回转中心的距离为R,r为导引头回转中心与转台回转中心的安装位置偏差,则安装误差示意图如图2所示[13]。
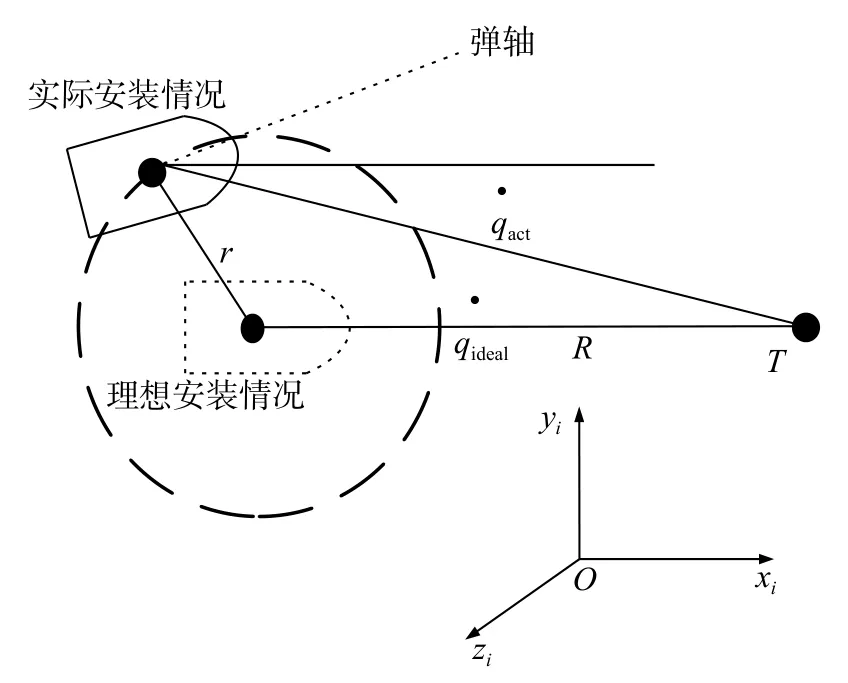
图2 导引头安装误差示意图
2.2 误差运动转换矩阵
转台系统可以抽象为多体系统,多体系统利用特有的低序体阵列来描述复杂系统。设转台基准坐标系为0体,则有转台安装系为1体,导引头体坐标系为2体,视轴坐标系为3体。对每个低序体分别建立体坐标系和运动参考坐标系,转台的运动可以等价于体坐标系相对于其运动参考坐标系平移和旋转[14]。
根据刚体旋转理论,各体序间的相对变换关系可由齐次坐标变换法来求得[15]。以导引体坐标系与转台安装基面坐标系为例。设由导引头安装误差引起的导引头体坐标系与转台安装基面坐标系间的轴系误差分别为 δx、δy、δz,则对应旋转矩阵为:
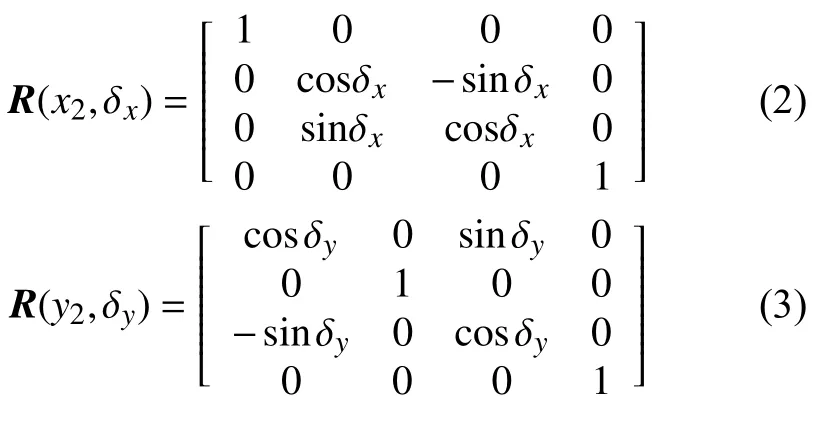
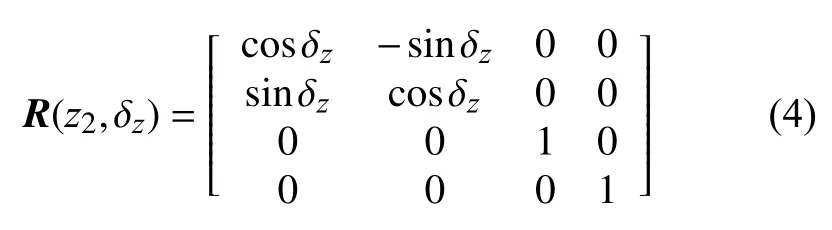
令:Tα=R(x2,δx)R(y2,δy)R(z2,δz),则Tα为导引头体坐标系到转台安装基准面坐标系的旋转变换矩阵。设导引头体坐标系原点在O-x1y1z1中的位置偏差向量为P(∆x,∆y,∆z),对应的平移变换矩阵为:

则导引头体坐标系到转台安装基面坐标系的变换矩阵为:T=Tr·Tα。
2.3 导引头安装误差建模
理想情况下,导引头体坐标系与转台安装基面坐标系重合,设转台回转中心到目标模拟器的距离为R,定义视轴在视轴坐标系内的指向矢量Q=(R,0,0)T,设t时刻下导引头理想视轴偏航角为qλ,俯仰角为qγ,则理想视轴指向在转台安装坐标系的指向向量Qideal=(qxi,qyi,qzi)T为:
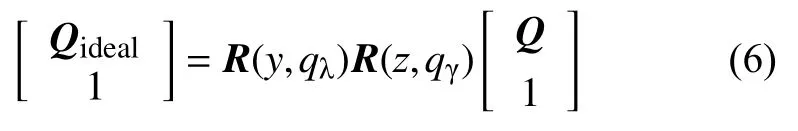
设此时三轴台内框、中框、外框的转角分别为γ(t)、φ(t)、θ(t),则理想视轴在转台基准坐标系中的指向向量可表示为
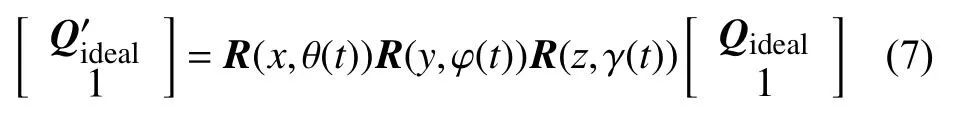
t时刻下导引头理想方位角与俯仰角为:
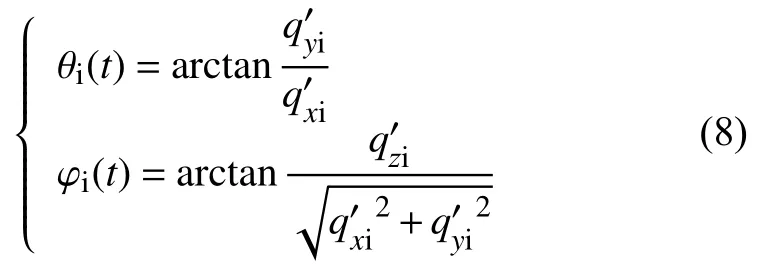
但由于红外导引头通过工装固定于转台的内三轴,将不可避免会引入安装误差,使得导引头体坐标系与转台安装基准坐标系不重合。当转台转动时,导引头也随之旋转相应角度,导引头体坐标系与转台安装基面坐标系的相对位置不发生改变,则t时刻下导引头实际视轴指向向量在转台基准坐标系下可表示为
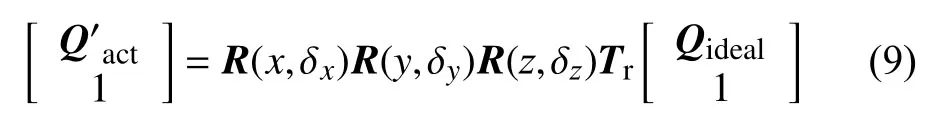
δx、δy、δz为导引头体坐标系与转台安装基面坐标系间的轴系误差,则可得转动后导引头视轴的实际方位角与俯仰角为:
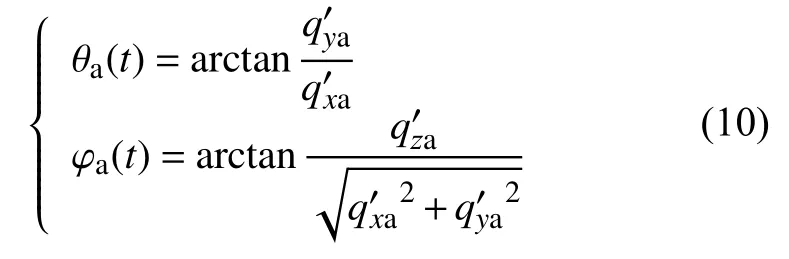
则由安装误差引入的视线角速度测量误差为:
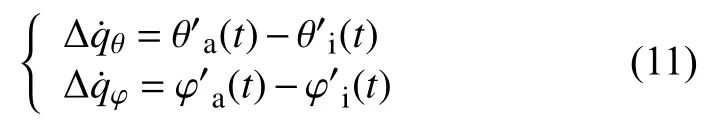
3 仿真分析
以俯仰方向隔离度测量为例,利用所建立的误差模型对导引头安装误差所引入的隔离度测量值误差进行仿真分析,设安装误差位置为 0.01m,导引头体坐标系与转台安装基面坐标系间的轴系误差为δx= 0.74°、δy= 0.2°、δz= 0°。设正弦扰动信号频率为 2 Hz,幅度为 1°,数据采集时间为1 ms。图3 和图4分别为干扰信号扰动角速度以及由安装误差引起的导引头视线角速度误差,可以看出由安装误差引入的视线角速度均方根误差为 0.002 12 (°)/s,此时由安装误差引起的隔离度均方根误差为0.019%。
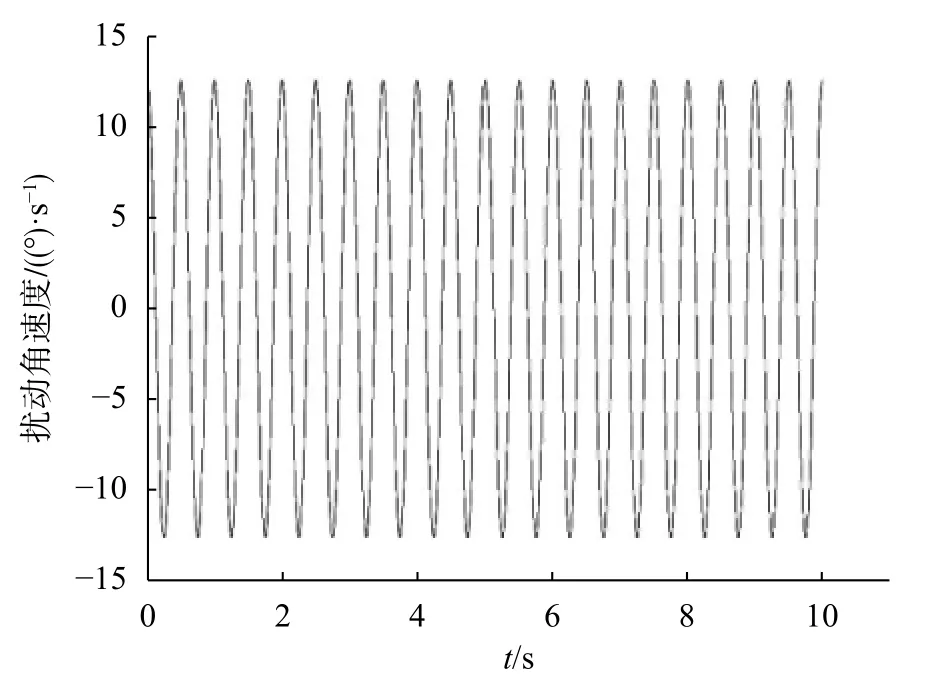
图3 扰动信号角速度
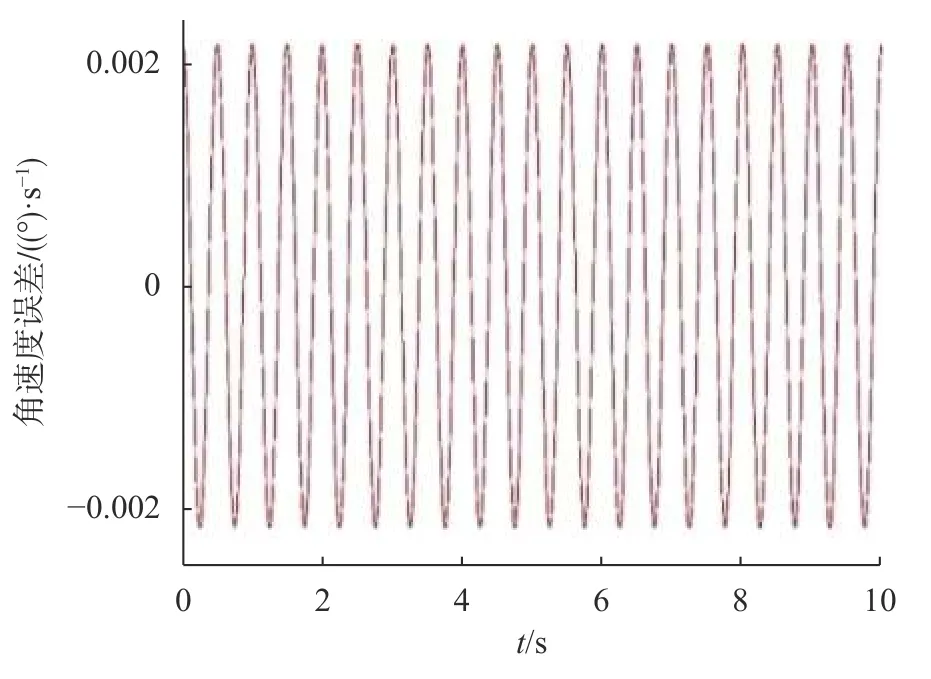
图4 安装误差引起的视线角速度误差
令导引头安装位置误差由 0.01m开始逐渐增大到 0.1m,此时由安装误差导致的最大视线角速度仿真误差以及隔离度误差如表1所示。
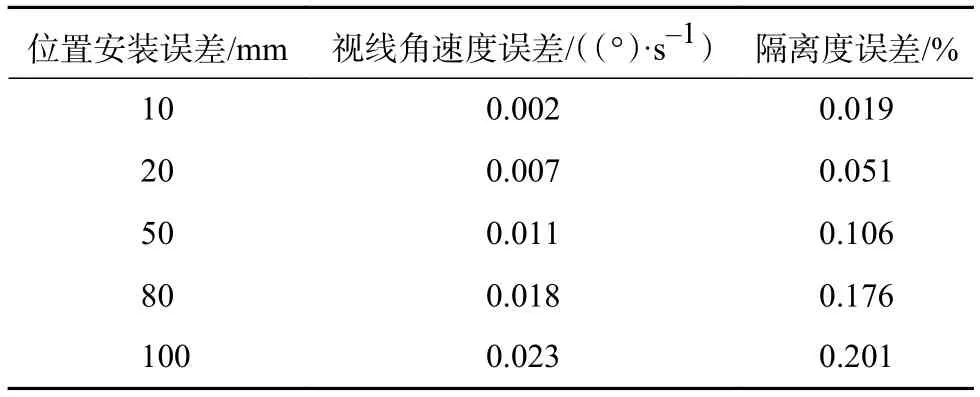
表1 安装误差引入的测量误差
由表中数据可知,位置偏差增大,引入的导引头视线角速度仿真误差越大,从而导致隔离度测量值误差增大。由于高精度导引头的隔离度要求一般在1%~2%,如不严格控制安装误差,必将极大影响隔离度指标的测试精度。必要时,需利用误差模型对安装误差引起的到隔离度测量误差进行补偿。
4 半实物仿真测试
本文采用某型号红外成像导引头进行半实物仿真测试。将其通过夹具安装于五轴转台的内三轴,此时可测得红外成像导引头实际安装误差为 0.062m,导引头体坐标系与转台安装基面坐标系间的轴系误差为 δx= 0.78°、δy= 0.26°、δz= 0.02°。
安装好后,采用第1节所述方法对其进行隔离度测试,导引头开机,转台寻零复位,令导引头锁定目标。
控制五轴转台内三轴的俯仰轴按照2 Hz、1°的频率和幅值进行扰动,系统数据采样时间为1 ms,并实时记录导引头输出视线角速度。
测试结果如图5所示,采用低通滤波器剔除导引头输出视线角速度中的噪声和毛刺,可求得导引头视线角速度为0.131 (°)/s,伺服系统隔离度为1.034%。
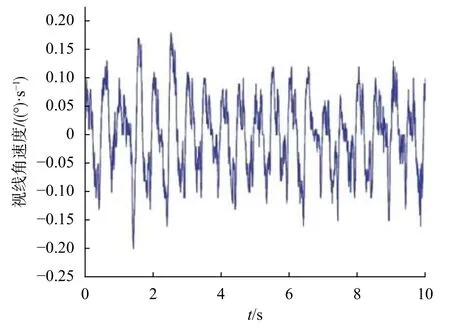
图5 导引头输出视线角速度
利用本文提出的安装误差模型可以求得导引头视线角速度输出误差如图6所示,得隔离度测量值的均方根误差为0.129%,误差百分比达到12%,已经无法满足高精度的测试要求。比较图5和图6可知导引头输出视线角速度与由安装误差引起的视线角速度在相位上不存在滞后,因此可认为由安装误差引起的视线加速度测量误差正向叠加到导引头输出角速度上,从而导致隔离度变差。这里得到的由安装误差引起所的视线角速度误差为复数,并与导引头输出角速度存在明确的相位与幅值关系,因此可直接相减。补偿后导引头视线角速度如图7所示,补偿后隔离度为0.902%,因此可采用本文建立的误差模型提高半实物仿真测量系统测量精度。
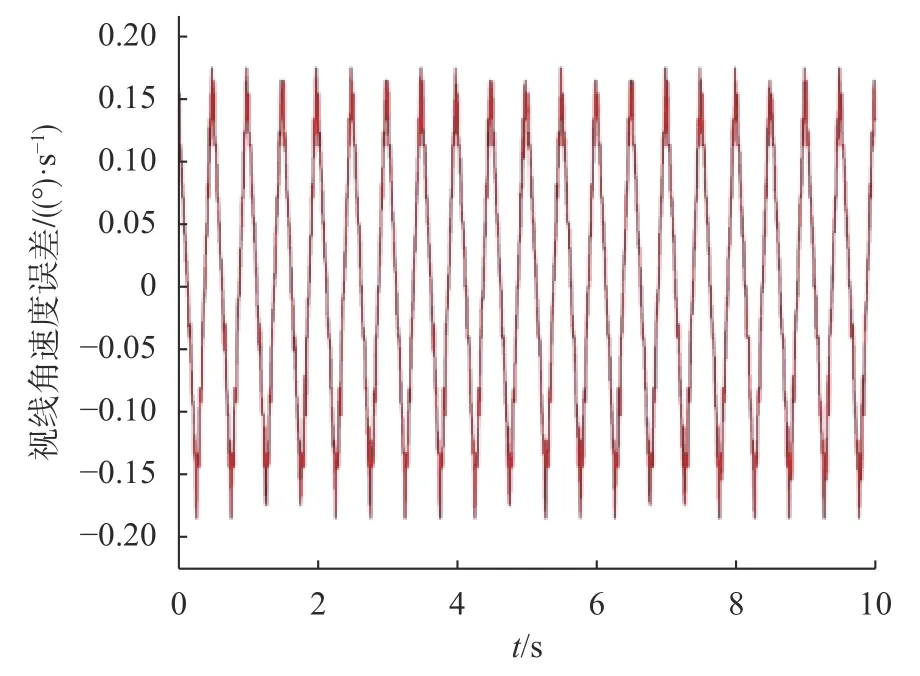
图6 安装误差引起的视线角速度误差
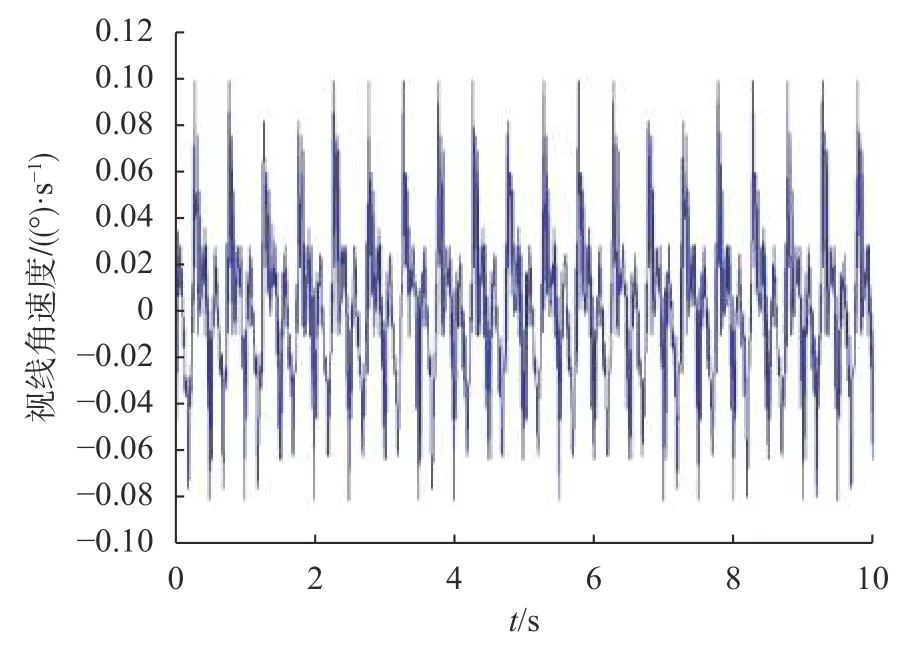
图7 补偿后导引头视线角速度
5 结束语
本文分析了由红外导引头安装误差引入的隔离度测量值误差,运用多体建模理论建立了误差模型。定量分析了安装误差对红外导引头隔离度测试的影响,并给出了一种补偿方法。仿真和半实物仿真实验结果表明,方法可有效补偿由安装误差引起的系统测量角速度偏差,提高导引头隔离度测量精度,且重复性好,测试效率高。这对解决红外导引头高精度指标测量问题具有指导意义,为在实验室条件下红外导引头关键战技性能指标的测试评价提供应用借鉴。
