基于PLS-SVR的电站锅炉NOx排放特性建模

马 宁，董 泽

(1.华北电力大学河北省发电过程仿真与优化控制工程技术研究中心，河北 保定 071003;2.华北电力大学控制与计算机工程学院，北京 102206)

0 引 言

随着对环境保护的要求越来越严格，减少污染物排收放已经成为燃煤电站面临的重要问题。其中，氮氧化物(NOx)是众多排放物中危害较大的污染物，也是导致全球变暖的因素之一[1]。因此，控制和减少电站锅炉NOx排放是十分必要的。燃烧优化技术是降低燃煤锅炉NOx排放的一种经济有效的方法。通过调整锅炉的给煤量、挡板开度、二次风量等可调参数，可以达到降低锅炉NOx排放的目的[2]。这种技术的基础是建立一个精准的NOx排放模型。然而，火电厂锅炉NOx生成机理复杂，各变量之间存在严重的耦合关系，因此，很难建立精确有效的NOx机理模型。基于数据驱动建模方法可以很好地克服复杂系统建模难题。近年来，建立燃煤电站锅炉NOx排放模型一直是众多学者关注的问题。牛培峰等[3]利用风驱动算法优化超限学习机参数对锅炉NOx排放模型进行优化，在一定程度上克服了超限学习机的不稳定性，取得了良好的预测效果。刘芳等[4]采用人工神经网络建立NOx排放模型，并实现了在线优化。然而，神经网络存在模型训练时间较长和“过拟合”现象。而支持向量机是一种以结构风险最小化为原则的建模方法，可以克服神经网络的不足。周昊等[5]提出一种利用核心支持向量机(CVM)建立基于大数据电站锅炉NOx排放预测模型。Si等[6]将改进的SVR应用于锅炉以及SCR脱硝的整体在线优化并取得了良好的效果。然而，影响锅炉NOx排放的因素众多，其中如给煤量、一次风量和二次风量等参数之间存在一定的相关性。若将这些变量直接作为模型的输入因子，势必会造成输入信息冗余，影响模型泛化能力。因此，在建模之前，对输入变量进行特征提取是很有必要的。

基于以上分析，本文提出一种基于PLS与SVR结合的电站锅炉NOx排放特性模型，即PLS-SVR模型。此模型利用PLS提取输入变量中的特征信息，将提取的特征信息作为SVR模型的输入，并以某1 000 MW超超临界机组现场运行数据为基础，建立了NOx排放PLS-SVR预测模型。

1 偏最小二乘和支持向量回归

1.1 偏最小二乘

偏最小二乘(PLS)是一种多元统计技术，通过将自变量与因变量之间的高维数据空间投影到相应低维空间，可以获得自变量与因变量之间的正交特征向量，再建立自变量与因变量之间的线性回归关系。与主元回归相比，PLS不仅有效地克服了常见的线性问题，而且在选择特征向量时还强调了自变量对因变量的解释[7]。

对于给定的自变量X=[x1,x2,…,xP]∈RN×P和输出变量矩阵Y∈RN×1，其中N是样本数，P代表输入变量维数。输入输出变量都经过归一化处理。经过 PLS 特征提取后的输入变量为T=[t1,t2,…,tA]，其中A为提取主成分个数，t1是由x1,x2,…,xP以线性组合的形式得到，称为第一主成分，其与输入变量X和输出变量Y的相关程度最大。经过对第一主成分回归后的残差项可以计算第二主成分t2，由此方法，可以得到所需的A个主成分，具体步骤[8]如下：

1）选择输出向量作为输出得分向量：u=Y；

2）计算输出权重向量w，并将向量单位化：wT=uTX/(uTu),w=w/||w||；

3）计算输入得分向量t：t=Xw；

4）计算输入负荷向量p：pT=tTX/(tTt)；

5）计算回归系数b：b=uTt/(tTt)；

6）计算残差矩阵：E=X-tpT,F=Y-bt；

7）用X和Y替换E和F，重复1）～7）直至残差项达到精度要求。

1.2 支持向量回归

支持向量机（SVM）是近年在机器学习、神经网络和模式识别等领域应用最广泛的算法，也是数据挖掘领域的十大经典算法之一，具有良好的应用背景[9]。SVM的基本思想是将原始线性不可分的训练数据集通过非线性方法映射到一个高维特征空间，使其变得线性可分，然后在该特征空间中找到一个具有最大分离距离的超平面。结构风险最小化的应用使得支持向量机具有更好的泛化能力。SVM开始用于解决分类问题，后来有学者将损失函数引入其中，这样SVM就可以用来处理回归问题。

支持向量回归（SVR）的具体实现方式为,首先将给定的数据集映射到高维特征空间，然后利用特有模型将样本映射到特征空间中，方程式为

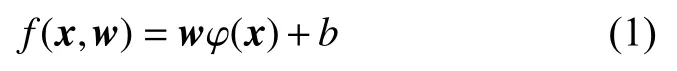
其中：w是加权向量，b代表偏差值。分类问题的核心是确定一个超平面将空间中的变量分离，而回归问题的关键是建立一个包含空间粒子变量最多的约束通道，这也是保证支持向量回归具有良好的泛化能力和预测效果的关键。本文选择径向基函数作为支持向量回归的核函数，径向基函数因其良好的应用效果被学者们广泛应用，其表达式为

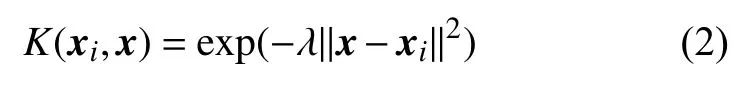
在使用径向基函数时，也要选取适当的 λ以及惩罚因子C和损失函数宽度。

2 电站锅炉NOx排放的PLS-SVR建模

2.1 锅炉介绍和数据准备

本文以某1 000 MW超超临界机组的直流锅炉为研究对象。该锅炉高度 65.5 m,截面 32.08 m×15.67 m,锅炉采用π型布置、单炉、改进型低NOxPM(污染最小)主燃烧器和MACT(三菱先进燃烧技术)型低NOx分级送风燃烧系统并具有双反向切线燃烧模式。水冷壁为内螺纹管垂直上升方式。

从电厂SIS（实时监控系统）数据库中获得锅炉运行约 31 h 的 1 867 组数据。采样间隔为 1 min，此采样周期已被证明是用于建立NOx排放模型的合适的数据采样间隔[10]。根据锅炉的基本知识和工程师的经验，确定了23个输入变量，包括机组负荷、6个磨煤机的给煤量、6个磨煤机一次风量、2个燃尽风开度、6个二次风挡板开度、二次风总流量和总风量作为NOx模型的输入，模型的输出是NOx排放量。所选择的变量及其范围列于表1中。由于所选工况下煤种相同，所以煤质特性并未被引入到建模变量中。通过调查，在正常运行条件下，机组在700～1 000 MW范围内波动，因此采样数据能够满足机组NOx排放建模的要求。

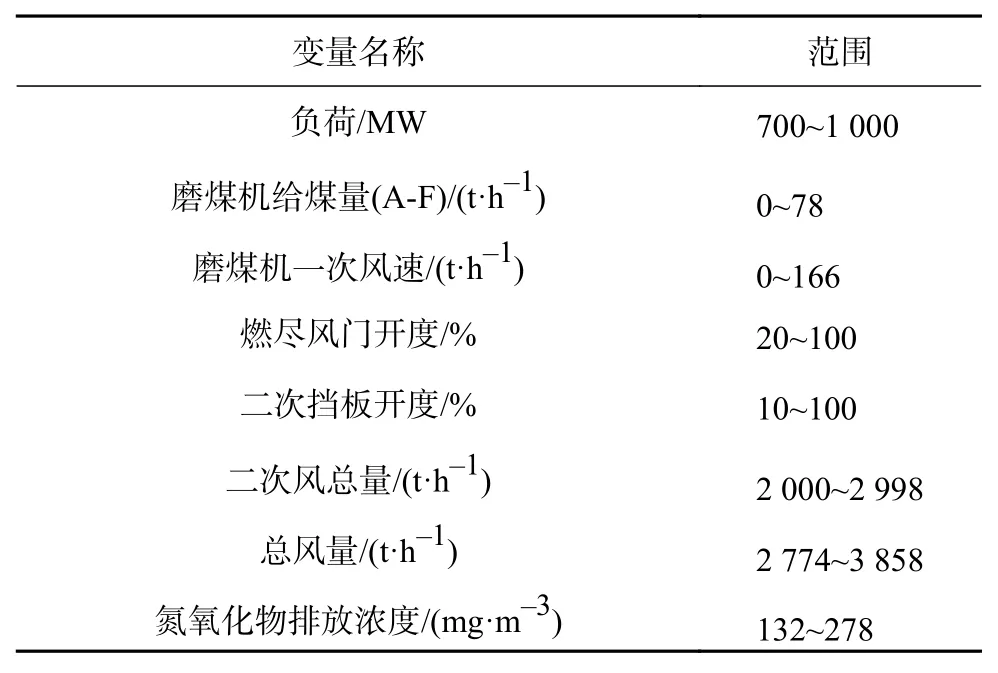
表1 各变量变化范围

2.2 建模过程

由于机组负荷、磨煤机给煤量和二次风流量等变量之间存在耦合关系，本文采用PLS提取输入变量的特征以减少变量维数和输入变量间的耦合，由PLS提取的特征矩阵代替原始输入样本作为SVR模型的输入。建模流程如图1所示。

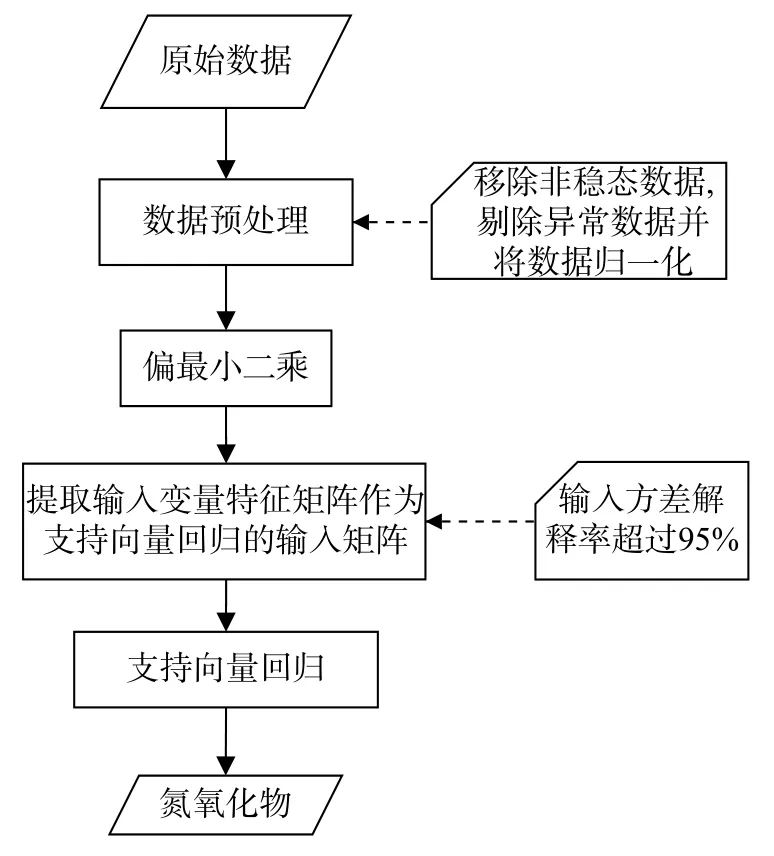
图1 PLS-SVR模型建模流程图

由图可知，在建立混合PLS-SVR模型之前，先对原始采样数据进行数据预处理。为了获得稳态条件下NOx排放模型，首先筛除机组负荷调整过程中的数据，然后将所有粗大值和异常值剔除。如图2所示，将剩余1 400组稳态数据分成两组，其中1 000组数据为训练集，用于训练PLS-SVR混合模型；其余400组数据作为测试集，用于验证模型。最后，为了消除各输入变量范围差异而引起的误差，将所有数据归一化，处理后的数据范围均在[-1,1]之间，模型输出结果将会反归一化。

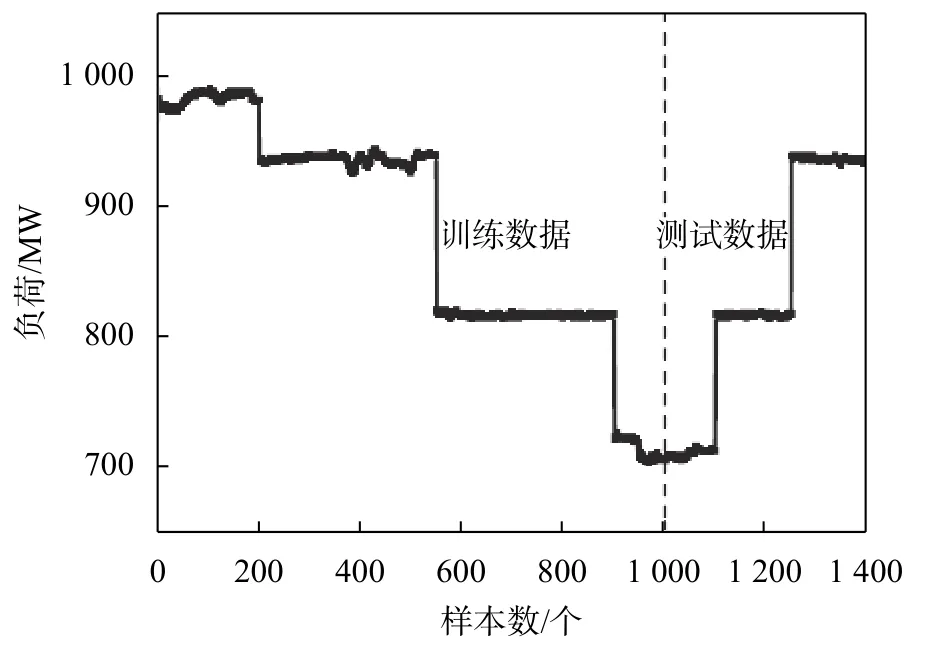
图2 采样周期内的机组负荷变化

经过数据预处理之后，利用PLS对输入变量进行特征提取，提取的主成分个数取决于各主成分对原始变量的累积解释率，具体地来说，假设当提取的主成分个数为A时，因变量中有95%的方差信息被解释，则不需再提取主成分。最后将提取后的特征向量矩阵作为SVR的输入，完成对NOx排放的PLS-SVR建模。此外，采用粒子群寻优算法（PSO）对SVR参数进行搜索并采用5倍交叉验证策略提高SVR建模精度。

3 电站NOx排放的PLS-SVR建模结果及对比分析

3.1 电站NOx排放的PLS-SVR建模结果

PLS-SVR混合模型通过PLS提取输入变量的特征信息来消除变量之间的耦合关系，减小输入维度，降低模型的复杂性。由此可见，PLS提取特征信息的过程是模型建立的基础，对于PLS-SVR混合模型的性能具有重要影响。图3为提取的主成分个数和各主成分的解释率。其中，提取的第一主成分的解释率达74.3%，前5个主成分累积解释率已经超过95%，因此此次建模过程中用于SVR模型输入的主成分个数为5。该结果也证明了未经特征提取的输入变量之间存在较强的耦合关系。

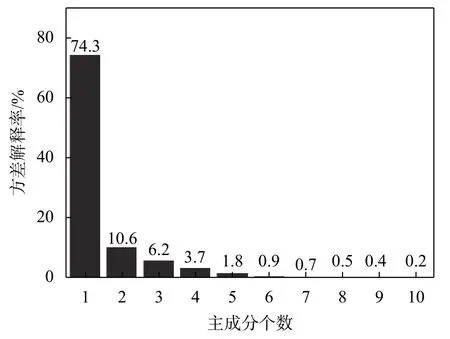
图3 主成分个数及其解释率

为了验证模型的泛化能力和预测性能，本文采用均方根误差（RMSE）和平均相对误差（MAPE）作为性能评价指标，计算公式如下：

其中，yi为实际值，yi′是模型的预测值，n为样本数量。PLS-SVR模型对训练样本和测试样本的预测结果如图4所示。从图中可以看到，无论对于训练样本还是测试样本，PLS-SVR模型的预测值曲线与实际值曲线的变化趋势一致，且能保持较小误差。图5给出了PLS-SVR模型对于训练样本和测试样本预测的误差曲线，从中可以看出，除个别工况点，PLS-SVR模型的预测值与实际值数据非常接近，误差范围控制在[-10,10]之间。这表明本文所建模型具有较好的预测能力。对于400组测试样本数据的模型精度为RMSE=4.072，MAPE=1.55%。整个建模过程耗时185 s。由以上实验结果可知，PLSSVR模型具有很强的辨识预测能力，能够对电站燃煤锅炉NOx排放浓度进行精确预测，且具有较好的实时性。

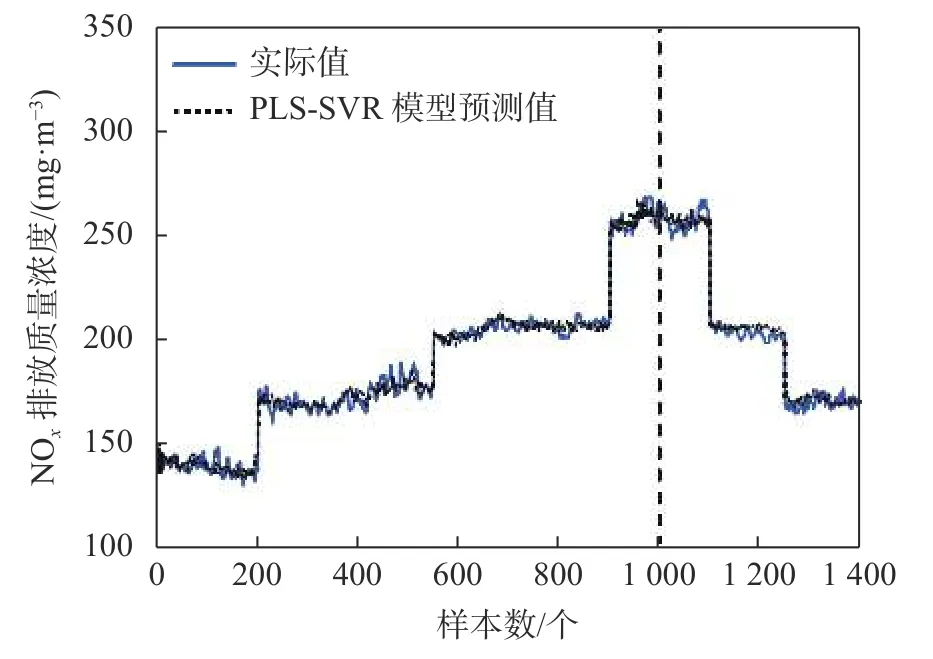
图4 PLS-SVR模型的预测结果

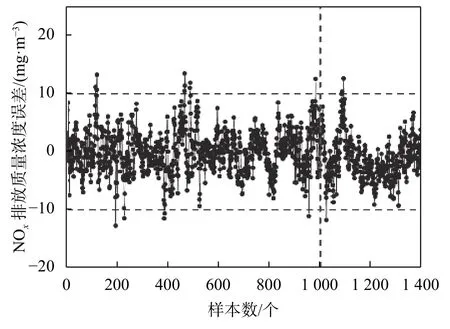
图5 PLS-SVR模型的预测误差图

3.2 模型比较

为了进一步验证PLS-SVR模型的性能，采用相同的训练样本和预测样本分别建立了SVR模型和人工神经网络（ANN）模型进行对比。与前文相同，在建模之前，先将数据归一化。ANN模型是具有单个隐含层的神经网络模型，其隐含层节点数的确定采用如下公式：

其中，l为隐含层节点数，n为训练样本个数。ANN模型的性能很大程度上依赖于模型内部参数，如输入层与隐含层之间的权值，这造成了ANN模型的随机性。为了得到精确的ANN模型，本文进行了400次重复的训练，整个建模过程耗时2 507 s。与PLS-SVR模型不同，单一SVR模型是将预处理过的输入数据直接作为SVR模型的输入，同样利用PSO算法优化SVR内部参数并采用5倍交叉验证策略提高SVR建模精度。表2给出了3种模型对于测试样本数据的预测结果和各自建模耗时。

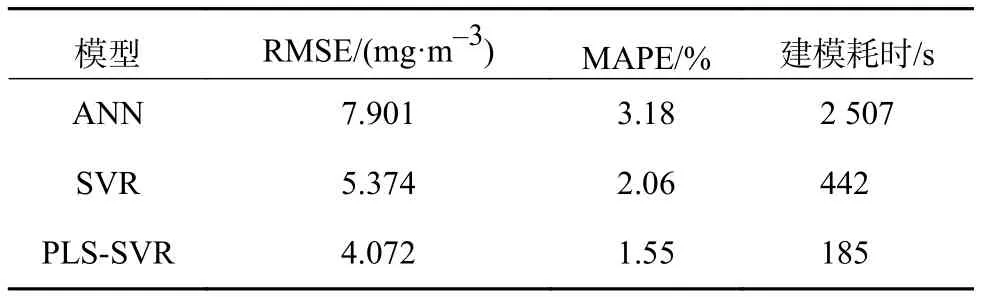
表2 3种不同模型NOx预测结果对比

通过表2中的计算结果可以看出，ANN模型的建模精度最差，对于测试样本的均方根误差为7.901 mg/m3,且耗时较长。单一SVR模型的预测结果为 5.374 mg/m3,低于 PLS-SVR模型的预测精度。此外，单一SVR模型的建模耗时也明显大于PLS-SVR模型，由此可以证明，本文所提出的PLSSVR模型通过PLS提取输入变量的特征信息降低了模型复杂度，提高了建模精度和建模效率。

4 结束语

影响锅炉NOx排放的变量众多且存在一定的耦合相关性，PLS能够有效地处理相关性问题，因此本文建立了基于PLS与SVR结合的锅炉NOx排放预测PLS-SVR模型。该模型通过PLS方法对输入变量进行特征提取，将提取的信息作为SVR的输入量。通过实际数据对PLS-SVR建模的有效性进行了验证并于与ANN模型和未经特征提取的SVR模型结果对比，结果表明PLS-SVR具有较强的的学习和泛化能力，PLS对输入变量的特征提取在提高模型准确性的同时降低了模型复杂度。