促进高阶思维发展的习题变式策略探究

浙江杭州市上城区时代小学 唐彩斌

山东烟台市芝罘区鲁峰小学 慕振亮

我国著名教育改革专家顾泠沅教授于1990年和2007年两次做了教学目标的大样本测试，对布鲁姆的教学目标分类进行了批判性的建设。 根据教学目标分类的层次性、分类的连续性与等距性，把认知目标及其对应能力表现水平描述为大致等距的四层次框架，分别是“操作、了解、领会和探究”四类目标，并给出了具体描述，形成了指向四个数学水平层次的框架。

在笔者组织的大样本区域小学数学质量监测的过程中，有一个发现：学生对于操作、了解类的低识知水平目标达成度较好，对于领会和探究类的高认知水平目标相对不足。 也就是说：我们常在低水平的层次高频训练，却在高阶思维水平层次低频发展。 适当降低这种低阶思维水平的“高频训练”，让学生有更多机会、更多时间去经历“高阶思维水平”的挑战，应该成为教学改进的方向。 也恰如郭华教授的观点：基于挑战、基于探究，是实现深度学习的主要途径之一。

那么，逐渐地从水平一“操作”、水平二“了解”向水平三“领会”、水平四“探究”过渡，这个转变的过程需要一种重要的策略就是“变式”。 《华人如何学数学》曾系统总结了中国特色的变式教学，把它视为“促进有效的数学学习的中国方式”，2020年国际数学教育大会将在上海举行，届时华东师范大学博士生导师顾泠沅教授将做大会报告， 可以预见“变式教学”将再一次被国际数学教育界聚焦。

那么，在新时代背景下，在国际视野下，作为一线的小学数学教育工作者，我们到底可以在实践层面如何更好地践行“变式教学”就变得更有意义，本文选择习题设计的小切口，提出几种常见的实践策略，努力将“变式”的思想付诸实施。

一、从直接变间接

思维具有两个基本特点，一个是概括性，一个是间接性。 在小学数学的习题设计中，由原来标准样式中的条件， 直接告知的条件改为间接条件，让学生在解决问题的过程中，自觉主动地把间接的条件变成直接的条件，沟通“间接”与“直接”之间的关系，从而解决问题。

比如，求长方形的周长。 已知：长方形的长是15厘米，宽是10厘米，周长是多少？ 这是一个标准样式的问题，学生的通过率在95%以上。把“宽为10厘米”改为“宽比长短5厘米”，问题变为：长方形的长是15厘米，宽比长短5厘米，周长是多少？ 就有学生会列式“（15+5）×2”求周长，因为在部分学生的认知水平里，求长方形的周长就是形如“（□+□）×2”可以求得的。 这就是水平一阶段，模仿性的操作，学生甚至不明白算理也在“依葫芦画瓢”。

除了把直接的条件改为间接的条件，间接性还表现在，将给出的信息转变成解决问题真正需要的条件。

比如有一条竖直的线段长20厘米， 以每秒5厘米的速度向右平移，1分钟后线段扫过的部分有多大？ 面对这个问题，需要学生自己识别“是求周长还是面积”？ 如果是求“面积”，那么是一个“什么图形的面积”？ 表象地思考出是一个长方形，那么还需要进而思考：“这个长方形的长是多少，宽是多少？ ”更有细节处还需要把1分钟转化为60秒，比起“一个长方形， 长300厘米， 宽20厘米， 面积是多少平方厘米”，间接的程度越高，对学生形成的挑战也越大。但是本着发展学生的空间观念和运算能力，以及综合解决问题的能力来说，显然，越是有挑战的问题学生的收获会越大。

二、从正向到逆向

20世纪80年代，赵裕春教授和张天孝老师等在全国组织了小学生数学能力的大规模检测。 当时就提出小学生重要的数学能力， 其中有一条就是：可逆性思考。 逆向思维的培养也是当下学生的一种重要思维素养。

记得笔者在英国访学期间，经常在英国的中小学听课，英国老师的课堂是这样的：7+6=？ ，8+4=？ ，9+7=？听着挺简单，突然提问：□+□=13。瞬间，学生的思维开放了。 这就是正向变逆向的最简单运用。还记得有一次笔者和美国的一位教师一起交流，他提到了数学课上的选择题，67+26，正确的答案是多少呢？ 学生说93，雷夫说：是的，正确答案是93。 那么，这个选择题的其他选项可以怎么填呢？ 可能是什么答案呢？ 学生补充说83，因为我有时会忘记“进位的”；马上又有学生补充41，因为有时会把加法看成减法的。 没想到明明知道了答案的选择题，逆向追问，也可以蕴含多种不同思考，依然有很好的教学价值。

在计算教学中， 带余数除法的正向习题，如13÷3=□……□，49÷8=□……□；正向变逆向，被除数和除数已知变未知，答案未知变已知，如□÷□=5……3，反而可以引发学生更多思考。

在图形与空间领域，绝大多数教师都有下面的教学感受：要求三角形的面积，正向题：三角形的底是15厘米，高是10厘米，面积是多少？ 逆向题：三角形的面积是150平方厘米，高是10厘米，底是多少厘米？ 显然，逆向题的挑战更大，正确率会降低10%。

最令人印象深刻的是应用问题，正向题：科技书有20本，故事书比科技书的2倍还多2本，故事书有多少本？ 逆向题：科技书有20本，比故事书的2倍还多2本，故事书有多少本？ 在逆向问题解决中，更需要学生的结构化思考以及更加复杂的推理，在这个过程中， 自然能增强学生更强的逻辑思维能力。

三、从封闭到开放

有学者研究，我们一般将数学开放性问题主要分为3类：（1）给出的问题条件是开放的；（2）问题的解题过程是开放的；（3）问题的最终结果是开放的。当然， 开放题也可以是这3种类型的综合情况。 比如，（1）条件开放题：问题的条件不完备或满足结论的条件不唯一：两个数相加为20，这两个数是多少？（2）结论开放题。 在给定条件下，结论不唯一：寻找13元6角的硬币组合？ （3）解题策略开放题。 思维策略与解题方法不唯一：围着火炉一圏，一次可以烤10个红薯，烤熟一个要5分钟，两面都烤熟才完全烤熟，现在烤15个红薯，至少需多长时间？ （4）综合型。在条件、结论、策略中至少有两项是开放的：一个长方形，剪掉一个角，剩下的部分还有几个角？

最为经典的开放题，是日本学者介绍的。 有一块长4米、宽3米的园地，现要在园地上辟出一个花圃，使花圃的面积是原来的园地面积的一半，问如何设计？ （日本开放题）：

教学中让学生尽可能多设计不同的图案并且独特、新颖，这就需要充分调用已有的知识和经验，突破原有的认知和思维定式。 显然这样的解题过程和最后的结果体现了数学开放题不同的开放类型，不同的开放程度能让不同能力和兴趣的学生得到不同的发展。 给予了学生表达自己数学观念的机会，使学生懂得了思维是一个过程而不是选择一个简单的答案， 开放题推动学生对问题的深层次理解，鼓励学生用不同的方法表示一半。 不同年级的学生都可以参与，并且可以有不同的表现。

笔者在教学“三角形面积练习”时，设计了一道开放题。

有两个正方形ABCD和FECG， 边长分别为8厘米和4厘米，G是CD的中点，E在BC边的延长线上。选择三个不同的三角形（非直角三角形）计算出面积。（最大的、最小的、中等大小的）

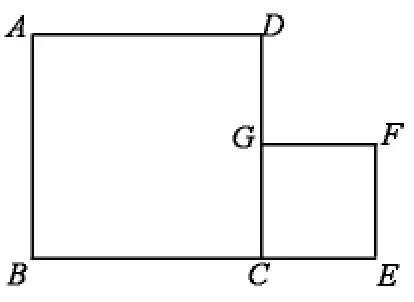
学生的作品中有简单的，有复杂的，低起点，人人可以参与，高落点，挑战性的三角形蕴含其中。 在找最小的三角形中，学生连起来三角形AGE,除了用整体减去部分来计算面积以外，还激发学生用“等积变形”的策略来解决，连接AC，AC∥GE，三角形GEA与GEC，同底等高，面积相等，而三角形GEC的面积方便可得：4×4÷2=8（平方厘米）。 一个问题情境中，引导学生深度思考，获得不同的发展。 提供这样具有适度开放性的问题情境，让学生可以从不同角度展开思考，进而提出不同的数学问题，培养思维的灵活性和发散性。

四、从单一到综合

从教学设计的角度来说，今天学的是A，练习的时候不能总是AAA,而是应该出现一个B，这样反而能加深对A的认识。学习周长之后，可以把面积结合起来；学习了进位加法之后，可以把退位减法结合起来；学习了归一问题后，可以把归总的结合起来。综合不是原有单一问题的简单罗列和堆砌，而是有机地融合。 比如，用一条长24米的篱笆，围出一个长方形花园。 要围出尽可能大的花园，长和宽分别可能是多少？面积是多少？此题中，既考查了学生对长方形周长的理解，也考查对面积的应用，这与传统意义上的已知边长求周长和面积相比，更加能提升学生的综合素养方面的能力。

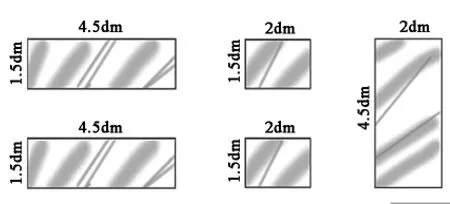
比如，用下面五块玻璃做一个鱼缸，这个鱼缸的底面积是多少？ 它能装多少升的水?(玻璃的厚度不计)

传统单一的问题都是直接提供长方体长、 宽、高的长度，求长方体的表面积和体积各是多少？ 这种问题就是平行叠加的“综合”，即A是A，B是B，将A和B融合起来综合考虑， 对于发展学生的思维能力助益不少。 单一的罗列变深度的融合，考虑问题的方面多了，筛选有用信息的层面高了，可以更好地锻炼学生的空间思维能力。

五、从静态到动态

从静态到动态，从变化到不变，要常常盯准变化之中不变的东西。 正是这些不变的东西，把变化中的不同镜头联系起来，从静态中衍生动态，在变化、变式过程中认识变化过程的本质，帮助我们去解决各种变化的问题。 要实现从静态到动态的变化， 对同一类数学问题我们不妨采用变换条件、变换问题、变换内容、变换形式、变换位置、变换叙述方式、变换解题思路等组成一道或几道新题让学生练习。

比如，在下面4个图形中，画出A向对边的高。

这4个三角形，问题都是画高，图（1）是标准图形图（2）（3）（4）变换了位置或形状，这是图（1）的变式练习，学生容易犯错。 通过把三角形移动顶点位置或变化形状， 通过标准图形生长出变式图形，在不断的变化中看到不变， 发现高概念的本质属性，深度理解垂直的两条线的位置关系，发展学生的空间观念。

比如，新图形的表面积有变化吗？

拿走一个小正方体，表面积比原来增加了还是减少了？

一个完整的长方体拿走一个小正方体，变化的不仅仅是体积单位，还有表面积的变化。 虽然从数量上看有变化，但变化是有规律可循的，前三种变化更多的是基于拿走不同位置的角块而实现学生思维从静态到动态的转变和思考。 从形式上看可以是多样的，而最后一种体积没有变化，但是表面积仍旧发生改变，变化的是物体的位置和面积，不变的是物体的体积。

六、从数学到生活

数学源自生活，又与生活处处相关，比如，某单位的围墙是正方形，外边长是200米，由石砖砌成，高度为3米，甲、乙两人分别从两个顶点出发，沿着外墙按逆时针方向步行， 如果甲每分钟走75米，乙每分钟走65米， 那么至少经过多少时间甲能看到乙？ 先按照追击问题来思考，距离差=一条边÷速度差=200÷（75-65）=20（分钟）。 这类问题的设计，就不同于传统的追击问题， 也不同于生活中简单的看见。 问题如此创设，挑战就增加了不少，思考空间增长很多。

比如，在教学“植树问题”时补充不是植树的植树问题：建德白沙大桥，全长约390米，在桥的两侧栏杆上每隔3米就有一头石狮子，桥头桥尾呼应，形态各异。 桥上一共有多少头石狮子？ 结合实际生活解决数学问题，学生常常疏忽“桥的两侧”。 联系了生活，提高了数学层面的挑战。

核心素养的一端连着现实世界，一端连着完整的人，在数学学习过程中，我们也要努力创设各种现实问题，引导学生在现实生活中应用数学解决问题，提升综合素养。