直击真疑问，力求真理解——“乘加（乘减）混合运算”教学设计之思考

浙江嘉兴市海盐县向阳小学 庄迎春

人教版二年级下册第五单元“混合运算”例2，是教学类似“7+4×3”的含有两级运算的计算课。 学生在学习本课前， 有过较长时间的两步计算式题（同级运算）的学习经历，即按从左往右的顺序进行计算，对此留下了深刻的印象。 强烈的思维定式，导致学生在本课学习中得知这类式题竟然要先算右边的乘法时，心里就涌出了一个巨大的问号：这是为什么呢？

教学中，很多教师这样告诉学生：“这是数学家规定的，先乘除，后加减。 ”然后组织学生根据规则进行强化巩固。 这样的教学，当场看似效果也挺好，但是随着时间的推移，学生根深蒂固的习惯就会消磨教师的“告诉”，到了三年级甚至到高段，学生还会出现运算顺序出错的现象。 笔者对辖区内一所城镇小学和一所农村小学的491名三年级学生进行了专项测试，结果如下表：

?

由测试数据可见，②④⑤题的运算顺序错误率是0， 而①③⑥题的运算顺序错误率都在20%左右，且学生的错误都是按从左往右进行计算。 这样高的错误比例，不禁让我们思考：先乘除后加减，学生为什么“记不牢”呢？

我们进行了分析，觉得以下两个原因也许是主要的。

图1

原因一：按教材编排顺序开展教学，使得学生对新知的形成感知不够。

教材（图1）的编排是从情境引入，学生读图后，看懂了每块跷跷板上有4人，有这样的3组，另外还有7人在观看。 此时，若要学生计算总人数，他们根据对情境的理解， 就已经想到了4和3是要相乘的，然后再和7相加。 因此，无论学生是列成4×3+7，还是在教师引导下列出7+4×3， 他们都已经默认了算式中需要先算乘法再算加法的。 如此一来，学生没有很好地感知到新知与旧知的差别，更没有深刻地经历新知形成的过程，知识的建构自然不到位。

原因二：告诉式的教学方法，使得学生对数学规定印象不深。

也许是教师们认为“先乘除后加减”的数学原理不适合小学生探究，或者认为理解其原理并不是本课的教学重难点，因此很多教师采用最简单的方式，直接告诉学生：“这是数学家规定的。 ”这样的做法，忽视了学生的认知规律，使得学生对这个规定产生的强烈疑问，缺乏一个释放、释疑的该有过程及深刻经历，以至于对数学规定印象不深，时间一长，难免就会遗忘。 简而言之，学生缺少了一段难忘的学习经历。

基于以上思考，笔者认为，本课的教学，教师应在学习过程的设计和教学方式的运用上动更多的脑筋， 要使学生对新旧知识产生强烈的认知冲突，暴露并聚焦对新知的真实疑问，开展积极主动的思考和探究，最终实现对数学规定的真正理解。 为此，笔者设计了如下教学环节：

课始， 出示两级混合的计算式题4×3+2和2+4×3，让学生独立计算，组织反馈。 第一小题学生都是先算4×3=12，再算12+2=14；第二小题2+4×3则出现两个不同的答案18和14。

师：一个算式怎么会有两个不同的结果？ 你们是怎么算的呢？

生1：2+4等于6，6×3等于18。

生2： 我是先算4×3， 再算2+12， 所以结果是14。

师：两位同学的算法不一样，谁的对呢？

生3：计算题都是从左往右算的，所以先算加法的对。

生4：我爸爸说要先乘除后加减的，所以等于14的对。

生5：我妈妈也说过要先算乘法。

……

师：同学们说的好像都很有道理，到底谁的对呢？ （学生都急切地看着教师）

师：老师告诉你，先算右边的乘法才是对的，从左往右算是错的。 （学生哗然）

师：同学们有什么想问的吗？

生（齐）：为什么要先算乘法？

师： 你们是不是都有这样一个大大的疑问啊？（学生频频点头）

设计意图： 由两道两级运算式题的计算引入，直接把学生对“2+4×3”的不同算法暴露出来。 然后放手让学生阐述各自的观点， 引发双方的激烈辩论，学生在争议中达到矛盾的聚焦：到底先算什么？接着，教师“郑重”地告知正确的方法，引发学生迸出真问题——为什么要先算乘法？ 整个环节，不断造势，步步紧逼，促使学生产生想探索原理的强烈愿望。

图2

出示情境图（图2），按（1）→（2）→（3）→（4）的顺序，分四步呈现完整的图，领着学生口头列式，逐步得出算式2+4+4+4。 （师板书）

师：答案等于多少啊？

生：等于14。

师：完全正确。 同学们能把这个算式再列得简单些吗？

学生独立列式，反馈。 绝大部分学生都列成4×3+2，学生说理。

生1：3个4相加可以列成4×3，再加2，就是4×3+2。

师：原来的加法算式中，2在最前面，你的算式中2到后面去了，看起来有点不一样。 有没有不同的列法？

图3

生2：2+4×3。 （有少数学生这样列）

师：这样对不对呢？

生：其实就是3个4和2换了一下位置，道理是一样的。 （师根据学生的解释适时板书，如图3，学生都认可这个算式）

师：这两个算式应该怎么进行计算呢？

随着学生回答，教师在黑板上形成板书如下：

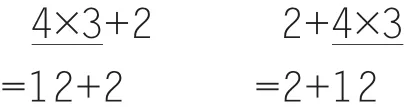
师：咦，乘法在前的先算，乘法在后的为什么也要先算呢？

生1：因为这两个算式的意思，都是2和3个4相加，所以都要先算3个4。

生2：其实2放在前和放在后是一样的，只是交换了位置，所以都先算4×3。

师：是的，有加有乘的混合运算中，乘法表示的是几个相同加数的和，它是一个整体，当然要先算。（板书：先乘再加）2+4×3的正确答案就是14。

设计意图：主题图上的信息依次呈现，引着学生口头列式， 可以让学生感受此类式题的原始状态，理解它的意义。 学生在计算中，自然会根据之前对乘法的掌握，主动选择用乘法进行优化，进一步增强“乘法比加法高级”的认识。 让学生列出与原来加法式子更“匹配”的乘法算式，目的是强化学生对2+4×3本质含义的理解。 通过计算以及之后的说理、沟通，学生真正地理解了不管乘法在前还是在后都应该先算的道理。

出示：1+5×3，3+2×4，2+3×3

请学生用递等式进行计算，反馈校对。 再选择1+5×3进行深入探究。

师：你能自己举个例子，用画图的方法表示出1+5×3的意思吗？

学生独立尝试，小组交流，展台展示作品（图略），交流。

生1：有3张5元的纸币，还有一个1元的硬币，一共有多少元？

生2：教室里有3排桌子，每排有5张，前面还有一个讲台。 教室里一共有多少桌子？

生3：老师分给3位同学每人5粒糖，手里还剩1粒，一共有多少粒糖？

……

设计意图：让学生用画图表征乘加混合算式的意义，这是一个变式的练习——逆向思考，目的是让学生调用已有能力，结合新课所学，更理性更深刻地建构“先乘后加”。 学生举出了丰富多彩的例子，通过展示与交流，更加直观、更加多元地支撑了学生对数学规定的理解。 由此，数学知识得以真正掌握，学习难点得以有效突破。

师：通过刚才的学习，我们知道了乘法和加法混合，要先算乘法，那么乘法和减法混合，应该先算什么呢？

图4

生1：我觉得还是先算乘法。

生2：我也认为先算乘法，再算减法，因为乘法比加法高级，肯定也比减法高级。

师分步出示（如图4， 棒棒糖是一根一根出现的），同步引领学生列出连减算式20-6-6-6。

……（教学展开略）

设计意图：由乘加两级混合向乘减两级混合顺向迁移，符合学生的学习心理。 教师设疑，学生猜测，在主题图的推进下，学生再次强烈地感受到乘法与减法在一起也要先算乘法的道理。 如此的学习，使学生对知识的应用（迁移），不是简单的机械模仿，而是更加深刻的理解和内化。

在小学数学教学中，类似于本课的规定性知识的教学内容还有很多。 作为教师，要站在学生的角度来看待学生心中的真问题，尽量避免简单化的说教或灌输。 教师要设法让学生提出自己的真问题，然后直击真问题，以合适的材料和形式，引领学生从数学本质的层面去理解这些规定背后的道理，使得规定性的知识成为学生水到渠成的认同。 我们相信，这样的教学，不仅能让学生更好地掌握知识，还会有效促进学生能力的提升。