学生提问，引之有方

浙江嘉兴市海盐县行知小学 俞 亚

在培养学生提问能力的过程中，首先是要让学生“敢提问”，这往往取决于教师是否给予学生提问的机会，简称“教师是否有意识”。 而真正让学生进一步做到“会提问”“善提问”，教师还需从意识层面上升到策略层面。

那么，如何引导，才能让学生有疑而问、问出精彩呢？ 我们尝试了以下几种方法。

一、释放已有认知，让问题在“深层猜想”中产生

在引导学生提问时，“见课题提问”是最常用的一种方法，它能快速将学生的求知欲由潜伏状态转入活跃状态，也是让学生提问的最简单有效方式。

有时候，我们也可以在出示课题后，不急于提问，而是先让学生尽情释放已有认知，积极调动知识储备，让思维得到充分展开，然后再来提问。

例如，教学“认识负数”一课时，出示课题“负数”。

师：见过负数吗？你在哪里见过？能写一个负数吗？ （让学生在自己的本子上写几个负数）

学生上台板书：-2，-1.5……

师：会读这些负数吗？ ……看来你们已经见过负数，也会读写负数。 那关于负数你还有什么问题想问吗？

生1：有负整数、负小数、负分数，有没有负百分数呢？

生2：为什么生活中会有负数呢？

生3：为什么要叫“负”数呢？

生4：负数是怎么来的？

……

我们发现，当教师设置了一个让学生释放已有认知的环节，延迟“见课题提问”之后，学生提出的问题就跳出了“是什么”“有什么用”等这一类概念课常有的普适性问题，从而出现了如对“负百分数”的联想、对“负”这个字的追问以及对负数来源的思考等一系列有价值的问题。

二、巧设矛盾冲突，让问题在“认知失衡”中产生

心理学家皮亚杰认为：“个体的认知发展是在认知不平衡时通过同化或顺应两种方式来达到认知平衡的，认知不平衡有助于学生建构自己的知识体系。 ”在数学学习中，教师要善于根据学生的认知特点和心理特征，提供能触发学生旧知与新知之间矛盾的材料， 打破其原有知识结构的平衡状态，促使学生表达心中疑惑，主动探究，重获平衡。

例如，在教学“三角形的内角和”一课时，学生基本都已经知道三角形的内角和是180度， 于是教师有意制造矛盾冲突，引发学生提问：

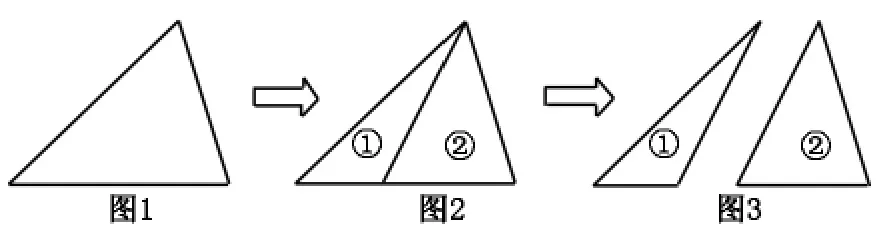
师：老师在这个三角形中（图1）添一条线，分成两个三角形，①号和②号（图2）。 现在将它们分开（图3），请问①号三角形内角和几度？

（学生有说90度的，也有说180度的）

师：那么，②号三角形呢？（学生有坚持说180度的，但已“底气不足”）

师：现在，你有什么问题想问的吗？

生1：为什么一个三角形的内角和是180度，分成两个三角形后，它们又都是180度呢？

生2：如果再分成更小的三角形，每个三角形的度数还是180度吗？

……

面对一节学生都已知道结论，看似没什么好上的课，教师没有遵循常规的教学方法，而是巧妙设置了一个让学生产生矛盾冲突的情境，触发了学生的认知困惑，学生的问题自然产生。 正是有了这样的疑问， 学生的学习才从被动验证变成了主动探究，课堂也从无趣变成了有趣。

三、梳理研究片段，让问题在“承上启下”中产生

心理学研究表明： 问题如果是经主体意识形成，就意味着主体更愿意花费劳动，通过自己的努力，获得问题的解决。 在课堂的推进过程中，当我们一个阶段的研究已取得初步的成果之后，往往需要向更深层次迈进。 这时，如果能激发学生进一步研究的兴趣，让其主动提出深入探究的问题，那是再好不过了。那么，如何引导呢？“梳理研究片段”的方法值得一试。 例如，“分数与除法”一课：

课堂围绕着学生提出的“分数与除法有什么关系”这一问题研究得出了一系列研究成果：

这时，教师小结梳理：同学们，刚刚我们通过画图、分饼等方法，得到了这么多的除法算式与分数之间有着相等的关系。 观察这些算式，你有什么发现？

师： 看来同学们已经发现了分数与除法的关系，那么，真的是这样吗？ 请你再仔细观察我们研究得出的算式，你还有什么疑问吗？ （停顿片刻）

生1：刚刚我们研究的都是小的数除以大的数，那么，大的数除以小的数，也会是这样的关系吗？

在上例中，如果教师没有梳理引导,分数与除法的关系研究也就止步于商是真分数的情况。 但是，我们看到，当教师梳理了研究片段，引导学生观察多个算式后，学生开始注意到了被除数与除数的大小关系，基于学习经验，他们马上想到了结论的确立还需要多角度验证， 于是，“如果被除数大于除数，结论是否还成立”这一困惑应运而生。 而对于这个问题的研究，让分数与除法关系的建立得到了全面的验证，“假分数”的理解也水到渠成。

四、捕捉对比材料，让问题在“聚焦本质”中产生

人们认识客观世界，把握客观事物规律，要通过探求事物与事物之间的异同，寻找事物之间错综复杂的内在联系来实现， 这就需要对事物进行比较。 在数学学习过程中，组织异中求同的比较，则有利于挖掘和显露知识的共性，使学生的理解深刻化与概括化。 引导学生提问，我们也可以从“比较观察”入手，尤其是学生的思维痕迹往往是非常好的对比材料，我们应该及时捕捉。

例如,数学拓展课《九宫的秘密》一课中，在学生尝试之后， 黑板上呈现以下几种学生摆出的九宫（如图4）。

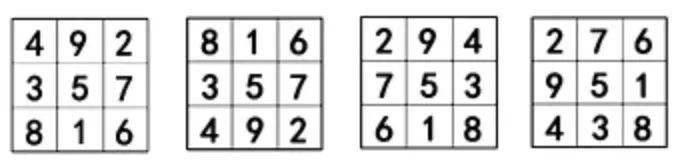
图4

经过教师引导，学生观察比较，讨论得出将第一幅图“上下对调”“平移变换”“逆时针旋转一次变换”等方法，就是后几幅图。 此时，教师组织学生提问。

师：看了这些方法，发现它们是可以相互变换的，现在你又有什么想法吗？

生1：那么如果顺时针旋转，不知道能不能也变成符合要求的九宫呢？

生2：如果旋转两次，可不可以呢？

生3：如果先上下交换，再旋转，是不是还对呢？

……

教师安排学生操作，检验交流，学生发现果然还有多种不同的摆法。

上例中， 教师通过呈现多种做法的对比材料，让学生的提问更有针对性， 也更聚焦于方法的本质。 另外，我们发现，在利用这种方法引导学生提问时，学生若能面对同伴的作品，则更能激发相互追问与解答的兴趣，也更能主动地对知识本质进行深入剖析，最终掌握知识内涵。

五、展示教材结论，让问题在“深度质疑”中产生

教材是学生学习的内容载体。 在平时的教学中，一般我们为了激起学生对新知更大的新鲜感与好奇心，总是特意创设一些情境引导学生步步深入、环环相扣地展开学习，而很少让学生翻开书本阅读教材上的内容。 其实，有时候，呈现教材上的一些结论或图示等，也能激发学生提出好的问题。

例如，《比的认识》一课，在教学这一课时，事先笔者让学生进行了预习。 在交流完学生已了解的内容之后，笔者出示了教材页面上的结论（图5），组织学生观察和思考。

图5

师：同学们，对于教材上的话你都理解了吗？你还有什么疑问吗？

生1：比的后项到底可不可以是0呢？

生2：不可以，因为你看上面不是说了吗？ 比的后项就相当于除法中的除数，除数是不能为0的。

生1：可是不对呀，我见过比的后项有0的。 足球比赛中，就有2∶0！

……

展示了教材上的结论，学生聚焦到了“比的后项可以是0吗”这个问题，他们自然能根据比与除法的关系理解比的后项不能为0，但同时生活经验也促使他们产生了深深的疑问：“为什么比赛中比的后项是可以有0的，而数学中的比的后项却不可以为0？ 比赛中的比跟数学中的比到底有什么不一样？ ”后续辨析区别的过程，不正是对数学中比的意义真正理解的过程吗？ 于是，课堂就围绕着学生的疑问而深入展开。

以上几种引导学生提问的方法，仅是我们在实践过程中摸索出的粗浅做法。 除了这些方法外，肯定还有更多的引问方法，我们将在后续的研究中进一步去探索与积累。