加强数学实验 促进深度学习

摘要：深度学习关注学生全身心积极参与、体验成功、获得发展。数学实验调动学生各方面的经验，促进学生手脑并用展开探索发现过程，是促进小学生数学深度学习的有效方式。数学实验教学要增强趣味性、凸显挑战性，通过具体的活动引发学生的高阶思维并持续加以运用，引导学生对实验过程和所获得成果的反思，在数学思想感悟和理性精神培育上也能获得发展。

关键词：数学实验;深度学习

中图分类号：G623.5 文献标志码：A 文章编号：1673-9094（2019）11A-0060-05

20世纪70年代，深度学习的概念引入教育领域，之后，相关研究成果不断丰富。对小学数学来说，这样的界定较为贴切：所谓深度学习，就是指在教师引领下，学生围绕具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程[1]。数学实验这个概念进入小学数学的时间也不长，但小学数学历来重视动手操作，鼓励学生手脑并用、学用结合，这些学习方式是数学实验的雏形。现在，一般认为，数学实验是在教师的引导下，学生运用有关工具，通过实际操作，在认知和非认知因素参与下进行的一种发现数学规律、理解数学知识、验证数学结论的数学活动[2]。

数学实验是小学生学习数学的重要方式，也是促进小学生数学深度学习的重要路径。通过数学实验，在教师的引导下，学生全身心深度参与具有探索性、挑战性、开放性的学习活动，在解决问题的过程中形成高阶思维技能、数学思维方法，获得数学活动经验，通过积极反思、自我评价将这些技能、方法、经验内化为自身的素养，提升能力，提振信心，获得发展。

一、数学实验引导学生全面投入，在情智互促中积极参与

人的深度学习是一种整体的学习状态，是学习者全身心投入的过程……它既是一个信息加工的过程，同时还是一个充满着情感、意志、精神、兴趣的过程[3]。数学实验正是这样的一个过程，它通常以一个具有趣味性或挑战性的问题为起点，引导学生动手实践、自主探索、合作交流，情感与智慧相互促进，全身心地投入数学学习活动，深度參与有意义的学习过程。

1.增强数学学习的趣味性，促进思考

兴趣是最好的老师，想让学生全身心投入学习，在学习起始阶段，想方设法激发学生的兴趣是一种十分有效的策略。当然，兴趣不仅应在学习起始阶段发挥作用，它应贯穿于学习过程始终。同时，学习过程也应不断强化并努力将其提升为持久的兴趣、长远的意志。数学实验的材料直观形象、可操作，能刺激学生的感官，诱发学生兴趣和思考，基于这些材料提出恰当的问题，使学生不由自主地参与观察、猜想、操作等活动，乐此不疲地展开数学思考。

比如四年级第一次学习“可能性”，教师出示两个不透明口袋，告诉学生，每个口袋里都放着两个球，形状、大小、材质都一样;指名一位男生、一位女生为代表，各用一个口袋做摸球游戏;每人每次从各自的口袋中任意摸一个球，摸出后放回，每人摸10次，谁摸到红球次数多，谁就获胜。游戏开始，学生注意力高度集中，男、女生都希望己方的代表能摸出红球。5次后，有的男生开始说，“不公平，我们口袋里都是黄球”，后来这种声音越来越多。游戏结束，男生、女生都迫不及待地说自己的猜想，“男生的口袋都是黄球，不可能摸出红球”“女生口袋都是红球，一定摸出红球”。教师打开口袋，验证了学生的猜想并提出问题：“口袋里怎样放球，才是公平的？”学生们说：“放一个红球、一个黄球。”于是，教师让学生们进行小组摸球实验，每组的口袋放一个红球一个黄球，记录10次任意摸球的结果。摸球结束，各小组展示自己的实验记录，说发现、谈体会，“我们组10次摸球，5次红球、5次黄球”“我们组6次红球、4次黄球”“都是第一次摸球，5个组中有3个组是红球，2个组是黄球”“这个组中间连续4次摸到红球”……最后总结：“口袋里1个红球1个黄球，任意摸1个，可能摸到红球也可能摸到黄球，不能确定。”

可能性是概率知识的初步，是一个比较抽象的概念。摸球实验（包括开始的演示游戏和后来分组实验）创设了一个有趣的问题情境，将可能性的知识隐含其中。学生因好胜而投入，因好奇而思考，因体验而感悟，情智互促，最后所交流的内容很好地反映出他们已经初步建构起对可能性的认知与理解。

2.凸显数学学习的挑战性，增强信心

正如苏霍姆林斯基所说，在人的心灵深处，都有一种根深蒂固的需要，这就是希望自己是一个发现者、研究者、探索者。对学生而言，发现、研究、探索的过程，就是一种不断接受数学学习的挑战的过程。通过数学实验探索规律、验证猜想、获得发现，都是能体验“跳一跳，摘到桃”的兴奋感，获得对学习本身的好感、对自我发展的满足感，以及因教师、同伴赞赏而获得的自豪感。

比如一年级教学“9+4”时，教师展示情景图“盒子里有9个桃（盒子有10格，1格空着），盒子外面有4个桃”，启发学生提出问题“一共有几个桃”，并列出算式9+4。之前，学生能计算10以内的加法，这个题对学生来说有一定的挑战性。教师引导学生通过数学实验发现算法：发给每个学生一张画有10格（2×5格）的纸和一些圆片;学生用圆片代替桃子，像情景图那样放好;然后思考“怎样才能知道一共几个桃？”并进行操作。有的学生这样“数”：把格子里、外的桃合并起来，数出共13个;有的学生这样“数”：盒子里有9个，盒子外从10开始数，10、11、12、13，共13个;有的学生“移”：把盒子外的1个移到格子里，凑满10个，10和3合起来是13……通过交流，学生都“喜欢”第三种方法，并根据操作过程抽象出算法：把4分成1和3，9+1=10，10+3=13。

进位加算法的核心是“凑十”，算理的核心则是对位值制“十位上的1表示1个十，也是10个一”的理解。题目本身的情景提供了一个典型的实验场景，具有暗示与启发性。学生通过操作、思考，主动发现了算法，并从不同算法中比较出相对更优的方法。师生互动、生生互动中的相互欣赏、表扬、鼓励，这些都不断强化了学生的自信心。

二、数学实验促进学生思维进阶，在深度认知中体验学习成功

数学教育要重点培养学生学科核心素养，包括学生的价值观、必备品格和关键能力，而思维能力又是关键能力的核心。深度学习不能脱离学科内容而展开，更为重要的是，深度学习应确保学生能够彻底地理解内容知识并能够识别何时、如何和为什么运用这些内容知识去解决新的问题……其中，如何、为何与何时运用知识，表现为批判性、创造性、合作性地运用知识解决问题，体现了布鲁姆教育目标分类学中的高阶思维技能[4]。学习心理研究的成果表明，成功感是学生内部学习动机的重要因素。奥苏伯尔认为，“成就动机是学习动机的核心”，并将成就动机区分为认知的内驱力、自我提高的内驱力和附属的内驱力[5]。数学实验作为小学生学习数学的一种方式，使学生有机会充分参与数学知识的发生和发展过程。在这样的过程中，学生能运用与发展高阶思维，在问题解决中主动建构新的认知结构，实现深度认知，体验学习成功。

1.任务驱动，引发高阶思维

高阶思维是发生在较高认知水平层次上的心智活动或认知能力。一些旨在让学生解决具有开放性、挑战性任务的数学实验，能让学生在相关的观察、操作、试验、调整过程中保持注意力高度集中，展开如分析、综合、评价和创造的高阶思维活动。

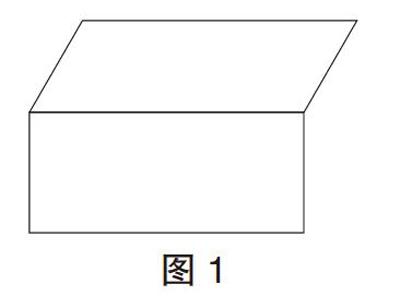
比如，五年级学习“多边形的面积”后，学生完成“动手做”的任务：画一条线段把平行四边形分成完全一样的两个部分。学生首先想到并画出平行四边形的对角线、对边中点的连线。接着，教师提高任务要求，“仔细观察，发现什么规律？还有其他画法吗？”有的学生发现这四条线段都经过同一个点（教师指出：这是平行四边形的中心），并提问：“会不会经过这个中心的直线都符合要求？”教师让学生试画并把分成的两个图形剪下来比较，发现完全一样。教师继续让学生完成任务：（1）用刚才的办法把长方形、正方形、正六边形分成完全一样的两个部分。（2）想办法把下面的组合图形（见图1）分成面积相等的两部分。学生很快解决了任务（1），对于任务（2），在教师指导下进行审题、讨论，反复试验、调整，也找到了方法，并总结出了相应的策略。

上述“动手做”的学习任务，具有开放性和挑战性。具体的材料、简洁的图形，有利于诱发学生在观察、操作中开展比较、分析、综合、概括等思维活动，在不断提出问题、解决问题的过程中，发现规律、提炼策略，促进思维进阶。

2.自主探索，运用高阶思维

如果说，任务驱动的数学实验更多是在教师主导下的学生所进行的，那么自主探索的数学实验更多是学生主体参与开展的。自主探索的数学实验，是小学生主动发现和提出问题，自主设计并实施数学实验，通过猜测、验证，凭借数学直觉创造性地解决问题。在自主探索的数学实验过程中，学生主动运用高阶思维，高阶思维的能力能得到巩固和加强。

比如，六年级总复习“图形的认识”中有这样一个题：把下面的正六边形分割成6个完全一样的图形。学生们尝试、交流，找到了两种分法：画出对边中点的连线，或者是对角线。教师用课件呈现了这两幅图（图2、图3），让学生观察，相互讨论能否有新的想法。稍后，一个学生举手发言：“对角线”的图，6个正三角形，“合”成3个平行四边形，每个平行四边形用另外的方法二等分。受到启发的其他同学纷纷动笔，又找到了2种分法（图4、图5）。教师问：“图3、4、5有联系，圖2、3之间的联系能看出来、想出来吗？”教室里安静了一两分钟，有人发言：“把对称轴“转”一下。”教师取出六边形教具和三根小棒，让学生在黑板上，先摆出图2的样子，再将小棒同时“转”动，到图3的样子。反复几次，学生恍然大悟：同时“转”三根小棒后停下来，得到6个四边形，是完全一样的。也就是说，有无数种的分法。教师用课件动画演示，停留后出现图6。

上述过程中，学生首先通过自主的动笔试验得到基本方法，对图形关系有了初步感悟，接着通过仔细观察、相互启发，由基本方法“变式”出新的方法，展现了一定的分析、综合与评价能力，最后通过展开空间想象、运用运动变化的思维对两种基本方法的联系进行深度发现，得到一般性的方法。这个过程中，学生借助实验的手段，对直觉思维的成果进行直观验证，具有创造的成分。

三、数学实验推动学生自我反思，在感悟内化中实现全面发展

以加德纳的多元智力理论为指导的全新的个性化的教学理念和最优的教与学的方式为我国素质教育的有效实施提供了良好的思路[6]，多元智力理论认为人具有“自我反省智力”，即个人认识、洞察和反省自身的能力。自我反省智力是学生实现深度学习的心理基础。小学数学中，这种自我反省智力，更多地表现为学生对学习的自我反思。有效的自我反思是建立在学生对所要反思的活动、事件、认知过程等有充分体验的基础上的，有了这个基础，学生不仅反思认识了什么，也反思是怎么认识的，同时强化伴随学习过程所产生的积极情感体验、态度养成，实现知识、能力与品格的深度协调与全面发展。

1.充分积累、感悟数学思想

小学生获得基本的数学思想主要靠感悟。《义务教育数学课程标准（2011年版）》指出，学生在积极参与教学活动过程中，通过独立思考、合作交流，逐步感悟数学思想。数学实验课的开展使学生的认知方式有所改变，学生需要参与教学活动，亲身体验数学知识发生、发展的过程，每个学生都可以自由地、大胆地猜想和实验验证，享受数学发现的喜悦、感知数学思想形成的生动历程[7]。小学生解决数学问题、感悟数学思想，既能加深对知识技能的理解和掌握，也能促进对数学知识、数学学习的正确认识。

比如，转化是一种重要的数学思想。小学数学中，多次让学生运用转化的方法解决问题、发现规律，逐步把握各种转化方法的本质，感悟转化思想。其中，又有多次是通过动手实验的方式进行的，并且每次实验都会引导学生回顾反思，突出对转化的认识，如五年级“多边形的面积”教学中平行四边形、三角形、梯形等的面积计算方法。学生面对新的问题，将平行四边形沿着高剪开拼成长方形、将两个完全一样的三角形拼成平行四边形、将两个完全一样的梯形拼成平行四边形，观察实验现象，思考转化前后图形的联系，推理得到新的面积计算公式。之后，教师都会引导学生回顾：“刚才是怎样得到平行四边形（三角形、梯形）的面积计算公式的？有哪些体会？”经过连续多次的活动参与和体会交流，到梯形面积的学习结束后，学生对转化思想的感悟达到一个新的高度，不仅初步体会到什么是转化，如何根据问题选择适当的转化方法，还将三种面积公式都置于转化思想的统领之下，增进对数学知识和数学学习的认识。

2.深度品味、升华理性精神

学生通过数学学习实现全面发展，与数学课程的学科特点、育人价值、基本任务相关。数学课程能使学生掌握必要的基础知识和基本技能，培养学生的抽象思维和推理能力，培养学生的创新意识和实践能力，促进学生在情感、态度与价值观等方面的发展。其中，“情感、态度、价值观的培养”是一个潜移默化的过程，即由理性思维逐步过渡到理性精神[8]。数学实验帮助学生丰富感性经验、强化直接经验，充分调动人的各种感官发挥作用，刺激大脑活动，引发学生的创新思考，对具体的数学知识、对普遍的数学学习产生深刻的、积极的认知并经历情感体验。

比如，五年级教学“小数的意义”，让学生通过小组合作实验的方式，依次探索三个问题：①一棵小树高0.7米，给你一根长1米的纸条，怎样表示出小树的长度？②如何在纸条上继续表示出0.73米的长度？③0.736米呢？对第一个问题，学生同桌合作，把纸条平均分成10份，1份是1分米，7份是7分米，是1米的7/10，是0.7米。教師顺势让学生认识0.1米到0.9米每个长度，并解释意义。接着学生探索第二个问题，把纸条上0.7米到0.8米之间再平均分成分10份，相当于把1米平均分成100份，1份是1厘米，73份是73厘米，是1米的73/100，是0.73米。同样的，教师也顺势让学生认识并解释如0.05米、0.74米等的意义。对第三个问题，有学生继续动笔，有学生则直接开讲，最后达成共识：0.73米和0.74米之间再平均分成10份，相当于把1米平均分成1000份，1份是1毫米，736份是736毫米，是1米的736/1000，是0.736米。经历了这一探索过程，学生对于小数的多元表征（比如：联系人民币的进率解释小数，把正方形10等分、100等分、1000等分来表示小数，把正方体10等分、100等分、1000等分来表示小数）、小数意义的归纳等感觉轻松、愉悦。更可贵的，最后教师问：“通过本课的学习，你有什么收获、体会？”学生答：“小数就是‘1不断平均分得到的;小数和分母是10的分数意义一样;只要需要，我们可以得到小数部分位数更多的小数……这样的认识，如果没有充分参与实验、操作、观察、思考、交流，是很难获得的;而这样的认识，恰恰是思维由感性到理性、由具体到抽象的过渡。经常经历此类活动，学生的理性精神将逐步得以发展。

总之，通过加强数学实验促进学生的深度学习，使教学过程中教师的主导作用与学生主体作用的发挥更加协调统一，让学生的学习更加注重手脑并用，更加凸显已有经验的激活与新经验的积累，促进学生整个人（包括情感与理智）积极投入学习，去尝试着发现得出新结论、学习难度较高的新技能、感悟更为一般性的新思想观念，获得学习成功的体验，实现品格与能力、情感与智慧的全面发展。

参考文献：

[1]郭华.深度学习及其意义[J].课程·教材·教法， 2016 （11）：27.

[2]董林伟，石树伟.数学实验工具：助力初中生数学学习的应然选择[J].数学通报， 2018（11）：1.

[3]吴永军.关于深度学习的再认识[J].课程·教材·教法， 2019（2）：54.

[4]张良.深度教学“深”在哪里？[J].课程·教材·教法， 2019（7）：35-36.

[5]皮连生.学与教的心理学[M].上海：华东师范大学出版社，2009：278.

[6] 钟启泉，崔允漷，张华.为了中华民族的复兴，为了每位学生的发展[M].上海：华东师范大学出版社， 2001：246.

[7]董林伟.初中数学实验教学的理论与实践[M].南京：江苏科学技术出版社， 2013：53.

[8]郑毓信.“数学深度教学”十讲之一——从“数学教育目标”讲起[J].小学数学教师， 2019（7/8）：10.

责任编辑：李韦

Mathematic Experiment and Deep Learning

LI Xin

（Wujiang Luxiang Experimental Primary School， Suzhou 215200， China）

Abstract： Deep learning pays attention to students wholehearted and active participation， experiencing success， and attaining development. Mathematics experiment can activate students all-round experience and promote their exploration and discovery with their hands and brains， which is an effective way to facilitate students deep learning in mathematics. Mathematics experimental teaching should strengthen interest and play up challenges. Besides， teachers may conduct concrete activities to trigger students advanced thinking continuously. Meanwhile， teachers should guide students to reflect on the experimental process and the achievements for their development in perceiving mathematics ideas and reasoning spirit cultivation.

Key words： mathematics experiment; deep learning

*本文系江苏省教育科学“十三五”规划2018年度课题叶圣陶教育思想研究专项“小学数学实验教学中儿童思维外显化的实践研究”（ YZ-c/2018/45）的研究成果。

收稿日期：2019-09-01

作者简介：李新，苏州市吴江鲈乡实验小学（江苏苏州，215200）校长，江苏省特级教师，中小学高级教师。