热连轧机轧制油对振动能量影响研究

裴令明

(马鞍山钢铁股份有限公司 安徽马鞍山 243021)

1 前言

某厂CSP轧机F3在轧制薄规格带钢时经常发生强烈的异常振动，导致轧辊产生振痕如图1所示。

改变轧制油的浓度[1]后发现振动信号有所变化, 为了对以上现象给与理论上的解释，利用有限元软件ANSYS建立了轧机有限元模型，应用功率流分析模块，研究在考虑润滑和不考虑润滑状态下轧机工作机座的振动能量变化。

图1 轧辊振痕照片

2 现场测试

测试所选钢种为Q235B、规格1250×1.8，分为7档浓度分别为：0.1%、0.15%、0.2%、0.25%、0.3%、0.35%和0.41%。测试结果如表1，0.1%浓度典型的PDA轧制力信号如图2所示。

为了更清晰起见，将表1制成图3所示。

表1 不同浓度下的轧制力

图2 浓度为0.1%时轧制力波形

从图3中看出：在轧制油浓度较小和较大轧制力作用下，很难形成油膜容易导致油膜破裂；当浓度继续增加时，油膜逐渐建立，故曲线先升高后下降。

3 轧制油浓度对刚度的影响

热轧轧制油是由基础油(矿物油)及部分油性剂和添加剂等组成。而矿物油的有效润滑温度范围一般为0-200℃[2]，含有大量冷却水的轧制油持续喷入轧辊与带钢的接触处完成冷却与润滑作用。

图3 轧制力随油浓度变化曲线

经四球机实验测得轧制油的最大无卡咬荷也即PB值为39kg。采用阿查得计算公式推算此力作用下的油膜厚度：

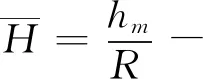
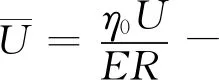
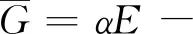
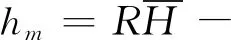
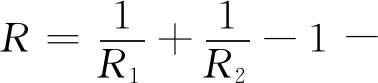
R1，R2-两接触体的曲率半径，cm；

η0-进口表面温度下的动力粘度，CP；

α=(0.6+0.965logη0)×10-3-压力粘度系数，cm2/kg；

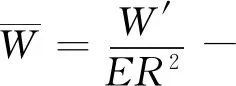
W′-接触点上总负荷；

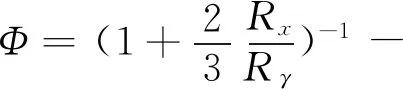
RX-沿运动方向的综合曲率半径；

RY-垂直运动方向综合曲率半径。

即当PB值为39kg时，油膜的厚度为0.01390μm，那么可以理解为当油膜厚度为0.01390μm时最大可承受39kg的力。此时可将油膜简化为一弹簧，那么此弹簧的刚度可理解为：

带钢的塑性变形刚度：

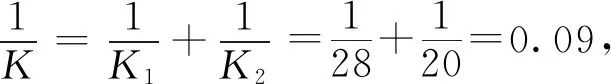
当带钢与轧辊间有润滑油进入时，为了方便分析，可将吸入的轧制油假设为弹簧，因此可把辊缝中的带材刚度和油膜强度形成的刚度看作一个整体。至此分三种情况来讨论轧机刚度的改变情况。

1)两工作辊直接接触，中间无带钢。

2)两工作辊间弹簧单元的刚度为20MN/mm。

3)两工作辊间弹簧单元的刚度为11.1MN/mm(加轧制油的状态)。

以轧辊最大尺寸建立的ANSYS模型如图4所示。

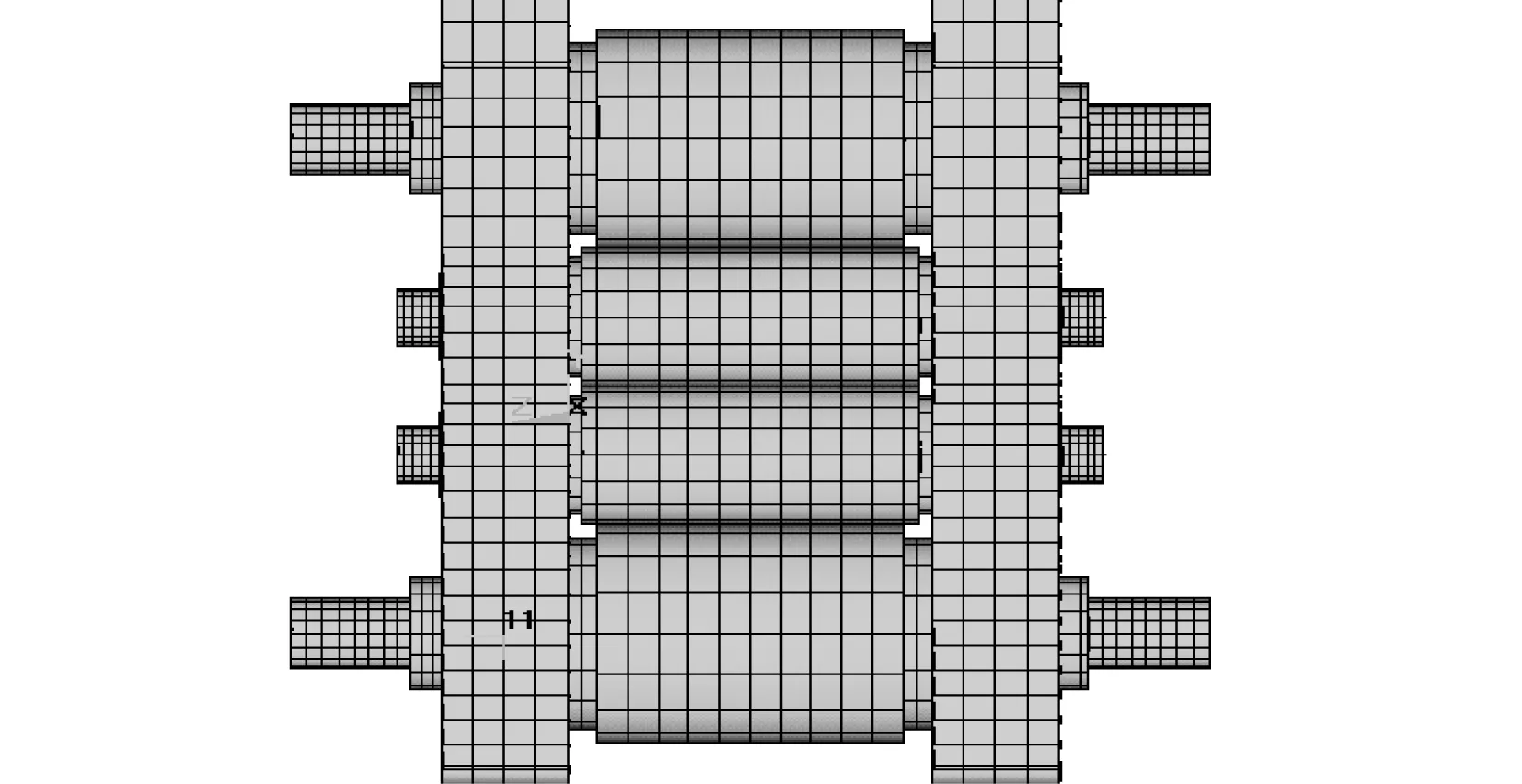
图4 无带钢轧机ANSYS图

对此进行模态分析，获得的前4阶固有频率如表2。

表2 三种情况下的固有频率(Hz)

由表1可以看出三种工况下的固有频率依次降低，第一种情况是两工作辊直接接触，接触的刚度可看作两工作辊接触刚度。第三种状态即加润滑油后的各阶固有频率比第二个只有带材状态要小2%左右，故得出轧制油可使轧机整体的刚度减小。

3 基于有限元的轧机功率流分析

振动功率流表示在单位时间内外力所做的功或结构耗散能量的能力[3]。

功率流法不仅考虑了传输结构上的力和速度两个值大小，也涉及到力和速度之间的相位关系，能有效地描述振动能量特性[4]。在弹性体中任取一点，则此点应力状态可用6个方向的应力分量来表示，即正应力σx、σy、σz和剪切应力τxy、τxz、τyz。取弹性体内任一微元来进行分析，其应力状态如图 5所示[3]。

在各种单元形式中实体单元是比较常见的形式，受到广泛应用。对实体单元来说，流经单位面积上的功率流为：

式中σn-法线n方向上的正应力，Pa；

τn1、τn2-1 和 2 方向上的剪应力，Pa；

vn*、v1*、v2*-法线n方向、1 方向和 2 方向上的复数速度的共轭，m /s2。

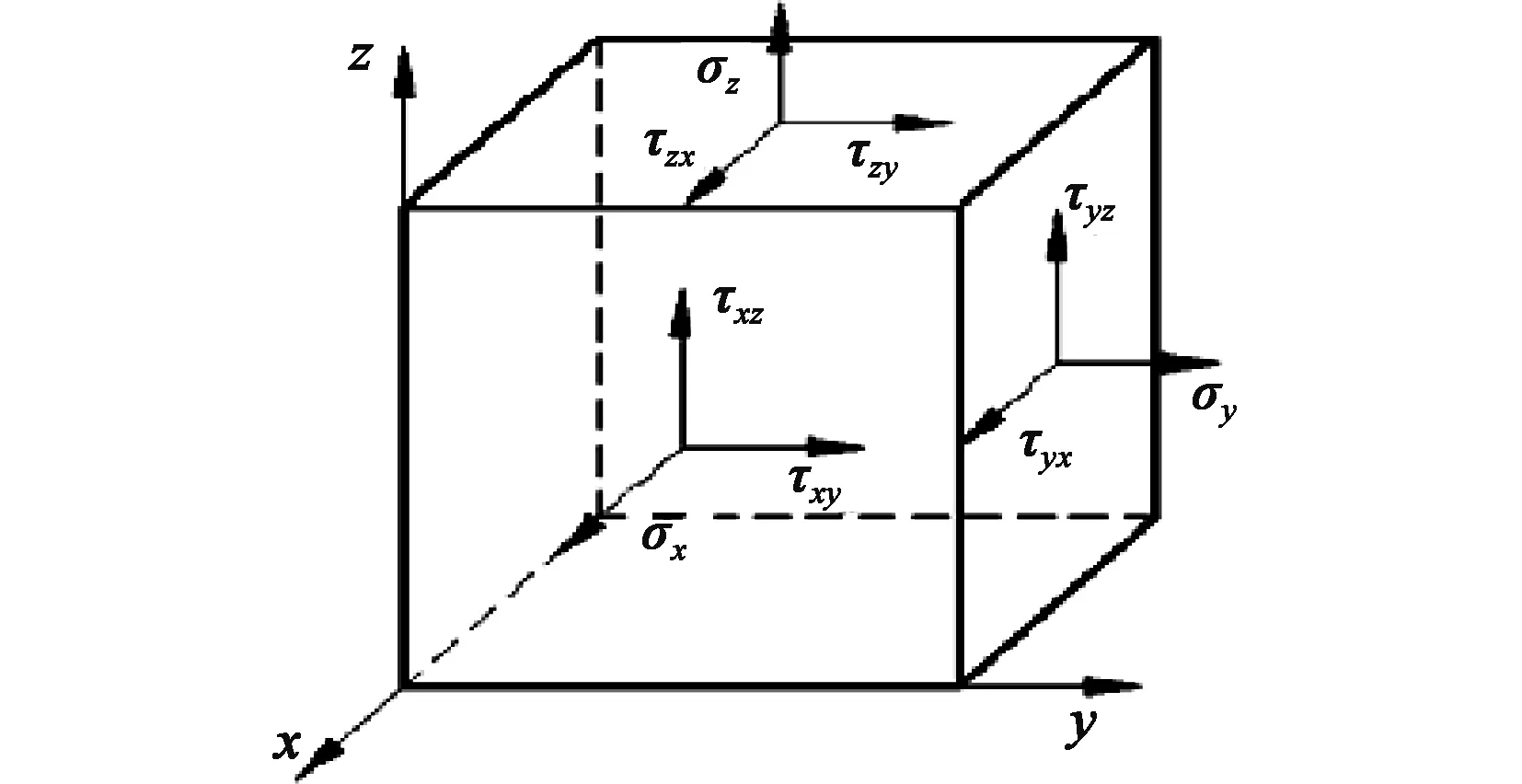
图5 弹性体应力形式

在实体单元上有x、y、z三个方向上的自由度，将单元功率流用应力和位移的有关参数表示为：

式中Px-x方向上功率流，W；

Py-y方向上功率流，W；

Pz-z方向上功率流，W。

据现场测试情况分两种情况来讨论能量。第一种情况：施加F=24000+400sinωt(kN)谐波，不考虑带钢和油膜刚度。

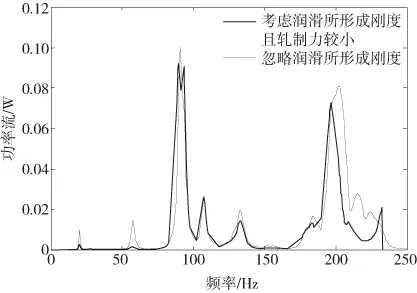
图6 上支撑辊轴承座功率流

第二种情况：施加F=25000+400sinωt(kN)，只考虑带钢刚度不考虑油膜刚度，选取和第一种情况相同节点号的位移和应力图形作功率流图 (为了便于比较将两图放一起)。

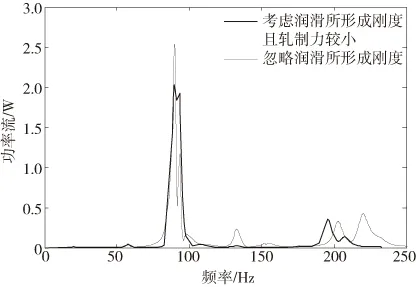
图7 上工作辊轴承座功率流

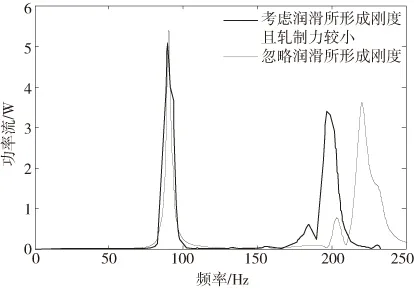
图8 下工作辊轴承座功率

结果表明：考虑油膜厚度情况和只有弹簧单元情况相比固有频率有所增大，而功率流的峰值和系统固有频率最大值所在频率相同，故第二种情况下峰值向高频方向移动，如图6-图9所示，并且当浓度增大时，功率流的峰值有不同程度的降低。

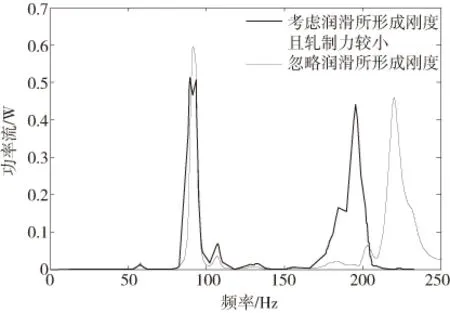
图9 下支撑辊轴承座功率流

4 结论

1)适当增大热轧轧制油浓度，可形成油膜降低轧制力。

2)所形成油膜刚度与带材刚度串联降低轧机刚度。

3)较低的轧制力和刚度使各个部件上功率流所代表的能量都有不同程度的降低，且有润滑时峰值所在频率较小。