辊系偏移距影响下的轧机非线性振动特性

凌斌辉 赵前程 凌启辉 邢洪羽

(1：湖南科技大学机电工程学院 湖南湘潭 411100；2：长沙矿山研究院 湖南长沙 410012；3：本溪钢铁(集团)有限责任公司矿业南芬露天铁矿 辽宁本溪 117014)

1 前言

近20多年来，随着热连轧机装备水平的不断提高，轧机出现了多种不同的振动现象，从而使轧机振动研究变得更加复杂。在轧制薄规格高强度带钢过程中，经常呈现轧机颤振、带钢表面振纹、轧辊表面印痕等多种不同、不确定性、不明原因的现象[1]。轧机振动不仅使带钢表面出现振痕，造成带钢厚度公差超出允许范围，也会在工作辊和支承辊的表面产生振纹后又加剧振动，进而影响后续轧制[2]。严重时引起堆钢和断带，造成废钢，同时还会损坏轧机机械和电气零部件，进而引发严重生产事故，严重地影响设备效能的发挥和连续生产，降低带钢的产量、表面质量和生产率[3]。

影响轧机振动加速度的因素很多，其中轧机辊系偏移距对轧机振动的影响不容忽视。本文通过构建轧机工作辊垂直-水平振动分析模型，利用数值分析的方法认识辊系偏移距对轧机振动加速度的影响。

2 轧机临界偏移距确定

为实现稳定轧制，通常四辊轧机的工作辊和支撑辊都会有一定的偏移距，辊系稳定性的条件为牌坊对工作辊轴承座的支反力Fs>0，根据文献[4]所给出的公式，可求得轧机辊系临界偏移距，有:

(1)

式中：FY为无间隙油缸对轴承座的顶紧力；ρ1工作辊摩擦圆半径；ρ2支撑辊摩擦圆半径；R1为工作辊半径；R2为支撑辊半径；FH为主传动系统附加弯矩引起的附加水平力；T1为带钢前张力；T0为带钢后张力；Pr为轧制力；z为考虑支承辊轴承处的摩擦及工作辊与支承辊间的滚动摩擦时，工作辊与支承辊接触处之反力偏离的一个滚动摩擦力臂的距离。

式(1)中各参数可参考文献[5-6]中介绍的方法来介绍，具体取值如表1所示，计算可得：偏移距e>3.72mm，某钢厂轧机实际偏移距为10mm，所以符合辊系稳定的条件。

表1 临界偏移距参数列表

3 考虑辊系偏移距的轧机动力学模型

考虑辊系偏移距后，支撑辊在工作辊上的作用力方向将不在垂直方向，而是与垂直方向成一定夹角。通过合理的简化，考虑到轧机系统辊系的对称性，本文只考虑轧机系统上工作辊的振动。轧机系统上工作辊及其轴承座为整体的力学模型，如图1所示，图中O1、O2为工作辊、支承辊圆心初始位置；kwr1为带钢和工作辊之间在水平方向的等效刚度；cwr1为带钢和工作辊之间在水平方向的等效阻尼；kwr2为带钢和工作辊之间在垂直方向的等效刚度；cwr2为带钢和工作辊之间在垂直方向的等效阻尼；kwr3为工作辊和支承辊之间的等效刚度；cwr3为工作辊和支承辊之间的等效阻尼；khar为牌坊立柱横向刚度；Fs为液压压下系统通过上支承辊给工作辊的支反力；Fc为工作辊轴承座与牌坊立柱间的摩擦力；Ff S为轧制界面摩擦在水平方向的分量；ω0为轧辊转频；△X为工作辊轴承座与牌坊立柱衬板间隙；e为轧机辊系偏移距；θ0为支承辊圆心在工作辊圆心垂直方向的初始夹角；θ为支承辊圆心在工作辊圆心在垂直方向的夹角；d为圆心O1、O2之间的距离；x为工作辊水平振动位移；y为工作辊垂直振动位移。

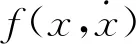
(2)

图1 上工作辊非线性动力学模型

工作辊轴承座与牌坊立柱之间的摩擦力Fc属干摩擦润滑，其大小与接触压力和摩擦系数μ1有关，有:

(3)

式中μ1——工作辊轴承座与牌坊立柱之间的干摩擦系数(取0.2)；

Fs1——液压压下力作用下，工作辊轴承座与牌坊立柱之间的正压力。

轧制界面摩擦跟轧制力波动量和轧制界面摩擦系数相关，有：

(4)

式中μ——轧制界面摩擦系数。

运用数学几何的知识可求得支承辊圆心在工作辊圆心垂直方向的偏角θ与振动位移x、y的关系，有:

θ(x,y)=(e+x)/(d-y)

(5)

依据工作辊动力学模型，建立振动微分方程为:

水平方向

=Fssinθ+Fws

(6)

垂直方向

=FωV+Fscosθ

(7)

式中m——上工作辊及其轴承座的集中质量。

4 数值仿真研究

本文将着重分析偏移距对辊系振动的影响。以辊系偏移距为分岔参数，系统位移响应、速度响应分岔图如图 2所示。为保证稳定轧制条件，辊系偏移距不能为零，工业实际一般为10mm左右。本文取辊系偏移距从(4～28)mm变化，系统水平振动和垂直振动的运动形态在偏移距等于(4～4.4)mm时表现为明显的倍周期运动，在偏移距等于4.4mm时分岔进入周期运动，经过短暂的周期运动后，在偏移距等于5.6mm时分岔进入倍周期运动，在偏移距等于21mm时分岔进入另外一种周期运动。

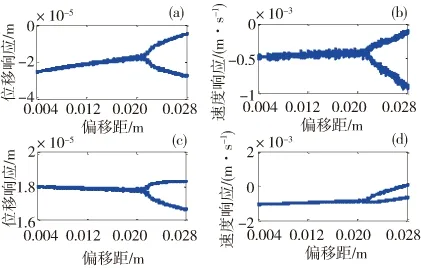
图 2 工作辊响应分岔图

为更好的验证辊系偏移距等于5mm左右时，系统发生周期运动，当取e=5mm，绘制系统的响应及频谱如图3所示，系统相图和庞加莱截面图如图4所示。从图中可以看出，系统的加速度主频除有激励频率的相同频率外，还有激励频率的2倍频和3倍频；放大相图，发现相图中有两个离散的点，说明系统运动形态表现为周期2运动。为更好的分析辊系偏移距对上工作辊振动大小的影响，分别以上工作辊的振动位移有效值和振动加速度有效值来描述振动强弱，绘制位移有效值随辊系偏移距的关系曲线如图5所示，绘制加速度有效值随辊系偏移距的关系曲线如图6所示。从图5可以发现垂直方向振动位移基本不随辊系偏移距的增大而变化，辊系偏移距在(4～21)mm变化时，水平方向位移有效值随辊系偏移距的增大而减小，在21mm时水平方向位移有效值最小，之后随辊系偏移距的增大而增大。垂直方向加速度有效值随辊系偏移距的增大而逐渐减小，减小的量值不大；而辊系偏移距在(4～21)mm变化时，水平方向加速度有效值随之增大而减小，在21mm时加速度有效值减小到5.61(m.s-2)，随后水平方向加速度有效值随辊系偏移距的增大而逐渐增大。

图3 系统响应及频谱(e=0.005m)

5 结论

本文以工业现场某热连轧机为例，构建了四辊轧机辊系水平垂直振动分析模型，通过研究辊系偏移距对轧辊振动的影响规律，得到以下结论：

(1)轧机辊系振动形态随着辊系偏移距的变化而表现出不同的振动形态，主要表现为周期、倍周期、分岔等振动形态；

图 4 系统相图和庞加莱截面图(e=0.005m)

图5 工作辊振动位移有效值与辊系偏移距的关系曲线

图6 工作辊振动加速度有效值与辊系偏移距的关系曲线

(2)轧机辊系偏移距从4mm～28mm的范围内变化时，垂直方向振动随着辊系偏移距的增大而减小，但不是非常明显；

(3)水平方向振动随着辊系偏移距的增大而先减小，到辊系偏移距为21mm时水平方向位移有效值最小，之后随辊系偏移距的增大而增大；

(4)通过数值仿真发现工业现场采用10mm偏移距不利于缓解振动，适当增大辊系偏移，轧机振动减小。