基于蒙特卡罗模拟的回购市场利率研究

陶浪平

（安徽财经大学，安徽 蚌埠233030）

一、模型与方法简介

（一）经典Vasicek 模型简介

相较于动态利率期限结构来说，静态利率期限结构认为债券的价格主要是受当前的即期利率影响，拟合的是当前的利率期限结构。然而，市场化的利率水平变动迅速，影响利率的因素绝对不止当前利率这一个因素。静态利率期限结构对市场的研究已经不能满足需求，动态利率期限结构也就应运而生。动态利率期限结构主要是对瞬时利率展开研究。瞬时利率就是剩余期限接近零的利率，通常用银行间拆借利率来代替。在动态利率期限结构模型的思想下，瞬时利率可以分成漂移项和波动项两个部分。具体形式如下：

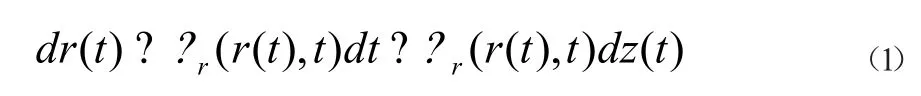
上式中，r(t)表示t 时刻的瞬时利率，ur表示漂移项，σr表示波动项。dz(t)是方程中唯一的随机项，其形式设为标准布朗运动。

在对动态利率期限结构的研究中，Merton 是第一个在利率期限模型中加入随机过程的人，他提出的Merton 模型也是动态利率期限结构中最基础的模型，莫顿模型把瞬时利率中的漂移项和波动项设为常数，具体的方程表达式如下所示：

莫顿模型在现实研究中存在的不足之处还有很多：例如，依据莫顿模型得出的利率可能出现负数的情况，不能保证利率的非负性；且在描述利率期限结构的动态变化过程中，莫顿模型也存在很大的瑕疵，如该模型不能刻画利率均值回归，以及利率波动率的特征；同时模型中通常将漂移项和扩散项设置为固定值，显然，这与实际经济市场情况不符。在单因子动态利率模型中，Vasicek（1977）在漂移函数项内加入了线性函数，与莫顿模型不同，瓦西塞克模型中瞬时利率漂移率的数值会达到历史平均水平，而经典的瓦西塞克模型是在莫顿模型基础上，引入了利率的均值回归项。Vasicek 模型的瞬时利率变化过程如下所示：

从(4)式中可以发现，Vasicek 模型会不断向利率均值靠拢。利率随时间的变化会不断向利率均值u靠拢，靠拢速度为回复速度k，Vasicek 模型中的常数值是σ，为模型的波动率。dz(t)为标准维纳过程。根据（4）式，可以推导出任意时刻T 的瞬时利率过程，具体形式如下：

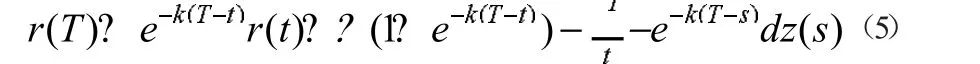
（二）基于蒙特卡罗模拟方法的国债定价

国债的定价法有很多种，不同国债定价法的原理各不相同，当前使用最普遍的国债定价方法，是先对利率模型进行参数估计，在估计出利率期限结构模型后，就可以得出债券的价格。由于这种定价方法需要运用风险的市场价格，而风险的市场价格主要通过人为的预先设定，也即市场风险价格的设定具有很强的主观性。基于减少市场风险价格等主观因素影响的考虑，本文采用蒙特卡罗模拟方法对国债进行模拟定价。

蒙特卡罗模拟定价法的基本步骤：

1. 利用估计出的单因子vasicek 利率期限结构模型，对利率路径进行模拟；

4.计算出债券在每一期的现金流，再根据前面求得的贴现因子，计算出债券的理论价格

与其他数值方法相比，蒙特卡罗模拟方法最主要的优点在于：该方法既可以用于当收益依靠标的变量终端值的情形，也可以用于当收益依靠标的变量路径的情形。

二、实证分析

（一）数据选取

本文选取银行间国债回购市场上质押式回购利率数据作为研究对象，采用了2017 年1 月至12 月的到期期限为一天的OR001 作为本文研究的即期利率数据，去除异常数据后，共245 条利率数据。通过对比其开盘利率、最高利率、最低利率及加权平均利率进行分析后，发现开盘利率，最高及最低利率可能会受到极端值的影响，因此我们选择加权平均利率作为本文的研究重点。

（二）差分图

在数据剔除异常值后，需要对数据的线性特征进行分析。本文采用SPSS 软件，对数据进行一阶差分，通过散点图来观察数据的线性特性。

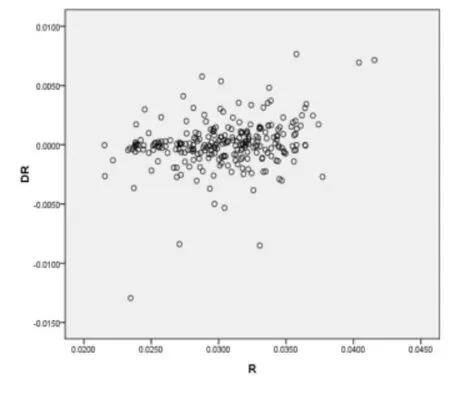
图1 DR001 散点图

首先对OR001 序列求一阶差分，求得一阶差分后得出一阶差分序列DR001，对DR001 绘制了散点图，通过散点图可以发现，数据总体呈现线性特征。

（三）数据的描述性统计

下表是对原始即期利率进行了描述性统计分析，通过均值、标准差、峰度以及偏度对数据的总体分布情况进行分析，不难发现数据总体分布态势平稳，数据的波动幅度不大。

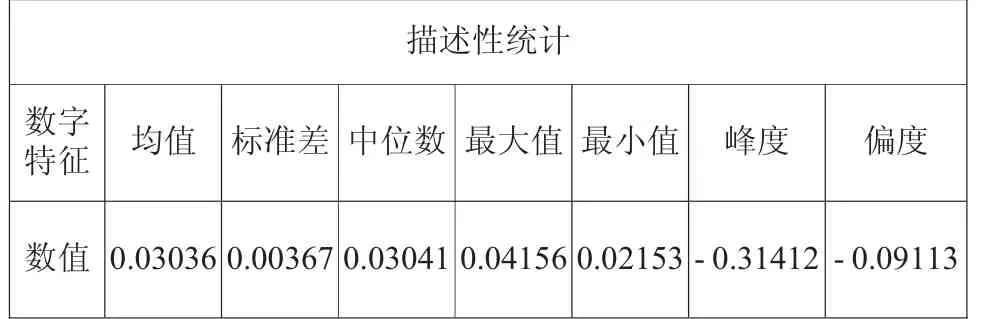
表1 描述性统计

（四）单位根检验

为了更好地反应数据的稳定性，本文又采用matlab 软件对原始数据进行单位根检验，结果如下表2 所示：

表2 单位根检验

表2 显示，数据伴随概率p 值为0.0002，其数值小于0.05，表明数据的稳定性良好。

（五）蒙特卡罗模拟的模型参数估计结果

1.参数的估计结果

由于本文使用的参数估计方法是蒙特卡罗模拟法，为了克服在模型参数估计中可能存在的误差，因此要在参数估计过程中先进行“退火”处理，去掉前面不稳定的计算结果。本文的选择的具体操作是去掉前10001 次的迭代，对参数引用后30000 次迭代。迭代结果如下表3 所示：

模型估计结果：

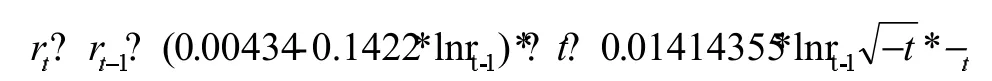
2.参数的收敛性检测

通过蒙特卡罗模拟，我们得出了模型的估计参数，然而，该参数是否有效？因为本文采用的是蒙特卡罗参数估计方法，参数是否收敛至关重要，只有当参数收敛时，其数据才是可用的，所以有必要对所得参数进行收敛性检测。参数收敛性检测可以分别从核密度图的平滑度以及参数迭代历史轨迹图的稳定性来分析。下图为三个参数的核密度图：

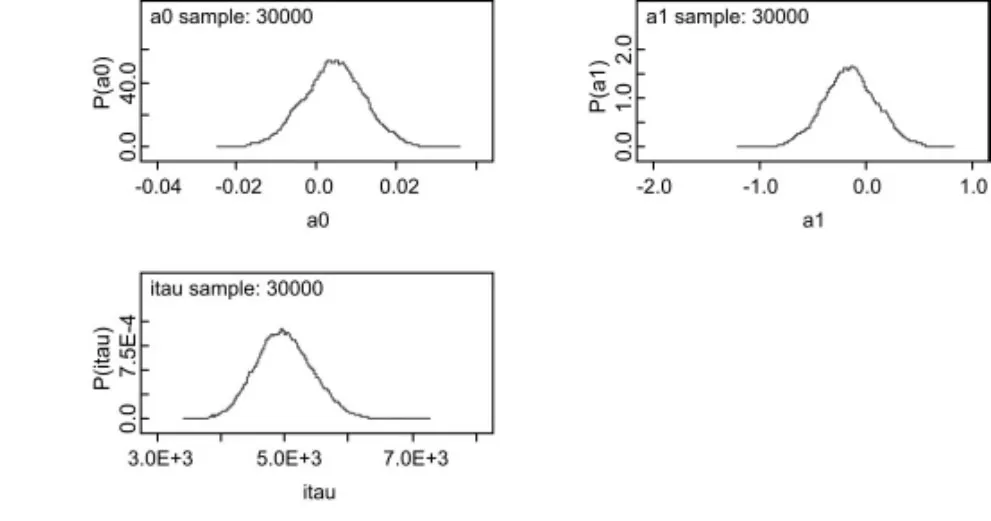
图2 参数核密度图

从上面三个参数核密度图不难看出，参数总体上是稳定的、收敛的。三个参数核密度图总体上来看都是相对平滑的，只是在部分区段表现出轻微的凹凸不平，但这也是符合实际情况的。并不影响参数的收敛性。

3.参数的迭代历史轨迹图

上文对三个参数利用核密度度进行了收敛性检测，接下来再对参数的迭代历史轨迹图进行分析。

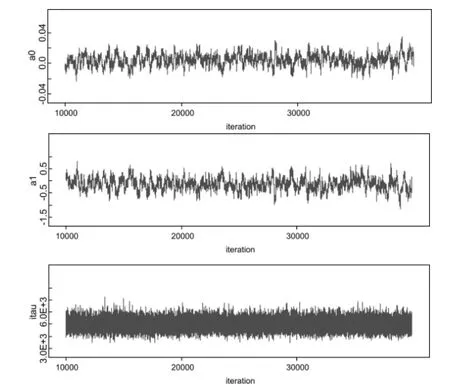
图3 参数历史迭代轨迹图

上图为三个参数的迭代历史轨迹图，通过这三个图可以看出，在去掉前10000 次迭代后，再进行30000 次迭代，发现这三个参数的均收敛，因此我们可以得出结论，蒙特卡罗估计法下得出的参数是有效的。

4.参数的动态路径图

下图4 给出了参数的动态路径走势，通过研究我们发现，三个参数值均围绕着其均值上下波动，并未出现发散或者明显的上升及下降趋势，因此参数的变动是稳定的。

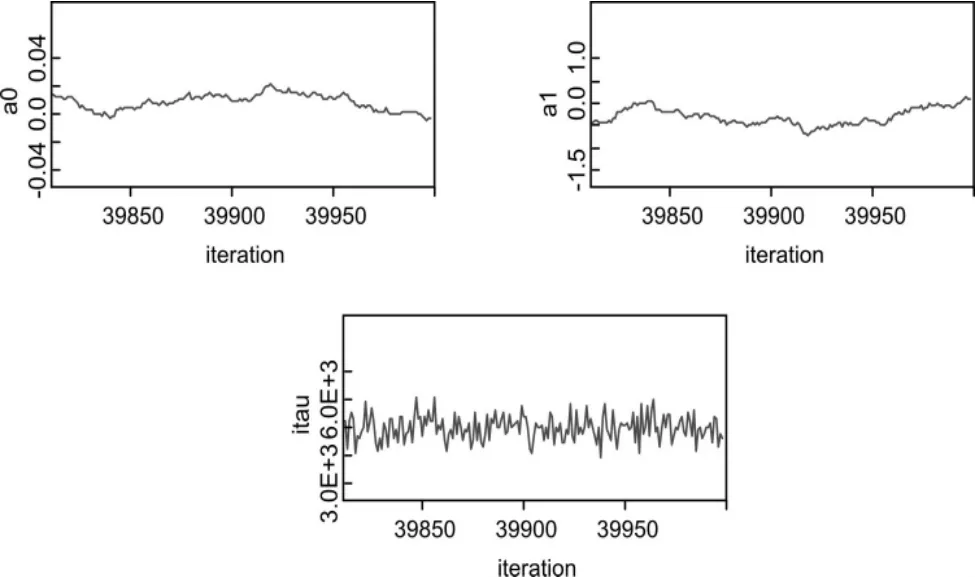
图4 参数动态路径图

综合上面对参数的核密度图、历史迭代轨迹图以及动态路径图的分析，不难发现，对于蒙特卡罗模拟得出的vasicek 模型的参数来说，参数都是严格有效以及收敛的。说明在利用蒙特卡罗法对模型进行参数估计的选择是合适的。

（六）利率路径

我们通过蒙特卡罗模拟估计出vasicek 模型的参数后，使用Matlab 软件编写程序，可以生成5000条利率路径，路径图如下图5 所示：

图5 利率路径图表明，随着迭代次数的增加，利率期限结构曲线趋于平稳，也就是说随着时间的变化，利率逐渐走向平稳态势。

三、结论

资金的价值体现在很多方面，而其时间效率的价值一直以来都是金融研究的核心问题之一，而描述它的重要工具就是动态利率期限结构。因此，动态利率期限结构必将是未来的研究重点。本文选用了2017 年1 月至12 月银行间国债市场的到期期限为1 天的质押式回购利率数据进行研究，从数据的一阶差分图、描述性统计以及单位根检验三个方面来对数据的稳定性进行全方位检测，发现数据是稳定的。然后利用蒙特卡罗法来估计vasicek 模型的参数值，并对参数值的收敛性进行检验。从参数的核密度图、历史迭代图和动态路径图发现，参数是有效且绝对收敛的。由此本文得出以下结论：

（一）本文利用2017 年1 月至12 月银行间国债回购市场数据进行建模，利用蒙特卡罗模拟对回购市场建立vasicek 模型的研究思路是合适的。

（二）通过散点图我们发现数据整体呈线性走势，对数据进行描述性统计后，发现数据分布均匀。对数据进行单位根检验，发现数据是平稳的。因此，我们可以得出结论：利用vasicek 模型对数据进行拟合是合适的。

（三）通过参数核密度图、历史迭代路径和动态路径图的分析，我们发现，利用蒙特卡罗模拟估计出的参数估计是有效的，且参数收敛性较好。