水平井钻磨管柱油管组合方式研究及下入安全性分析*
2019-12-12陈文康杜宇成孙巧雷
陈文康,冯 定,杜宇成,孙巧雷
(1.长江大学 机械工程学院,湖北 荆州 434023;2.长江大学 湖北省油气钻完井工具工程技术研究中心,湖北 荆州 434023;3.长江大学 非常规油气湖北省协同创新中心,湖北 武汉 430100)
0 引言
各大油田趋于通过延伸水平距离,增大油气层的裸露面积实现增产[1-2],故导致作业井身的水平段长度不断增加、水垂比逐渐增大,钻磨管柱在下入过程易造成遇卡、锁死等事故[3-4]。针对钻磨管柱下入困难问题,国内许多油田采用了2种线重油管的组合方式进行钻磨作业,通过改变直井段和造斜段的油管重量,增大管柱的有效推力,提高了管柱的下入能力[5-6]。但钻磨管柱组合方式的下入能力提升机理、下入载荷变化规律、2种线重油管组合方式优选的依据以及钻磨管柱下入性等问题尚无系统性研究。
基于此,本文首先根据钻磨管柱存在多变径部位的特点,充分考虑井眼轨迹及管柱内外壁与流体间的相互作用力,利用微元法将整个钻磨管柱离散为n-1个单元,进行受力分析,建立钻磨管柱的下入载荷计算模型;其次对油田水平井进行实例计算,将计算结果与实测结果对比,验证模型计算的正确性;最后以此为基础,展开钻磨管柱组合特性研究及参数敏感性分析,找出2种线重油管组合方式最优选择的依据和载荷变化规律,对于保障钻磨管柱安全下入具有重要意义。
1 钻磨管柱下入载荷计算模型的建立
1.1 钻磨管柱下入性的理论分析
钻磨管柱在下入过程中不能到达预定位置主要有2个关键因素:1)钻磨管柱在多种载荷的联合作用下管柱的轴向分力大于其产生的摩阻力,此时钩载力为正,认为钻磨管柱可以下入,当钩载力为负时,钻磨管柱受阻则无法下入,若强行下入则会造成管柱断裂等事故[7-8];2)钻磨管柱在井筒内发生“遇卡”,其中扶正器的刚性和外径较大,不易随管柱发生弯曲变形,使钻磨管柱无法继续下入[9-10]。
为了使钻磨管柱能达到预定位置,钻磨管柱采用油管组合方式,结构如图1所示,图中R为斜井段的曲率半径;γ为狗腿脚,l0和l1分别为直井段和水平井段长度,m;Δα为管柱微元段上下截面上的井斜角差值。

图1 钻磨管柱组合结构Fig.1 Joined structure of drill-grinding string
1.2 钻磨管柱内外壁与流体间的相互作用力
在模型建立之前需做出如下假设:1)由于工具串的长度远小于管柱的长度,因此工具串后端水平段油管视为与井筒连续性接触;2)管柱的轴线与井眼轨迹的轴线一致;3)由于磨鞋工具和扶正工具直径最大,因此将其简化成铰链;4)钻磨作业流体为牛顿流体。
考虑钻磨管柱下钻过程内外流体与管壁间的相对流速较大且流体存在粘性阻尼作用,管壁与流体间会产生相互作用力[11-12]。建立流体单元受力模型,其中单元长度的管柱内外流体沿程水力损失为:
(1)
(2)
式中:hf外,hf内分别为管柱外、内流体沿程水力损失,m;β为不同流态的系数;δ为不同流态的指数;v为运动粘滞系数,m3/s;L为管柱单元长度,m;D为管柱外径,m;S为过流面积,m2;V为流速,m/s;d为管柱内径,m。
考虑2种线重油管的连接处和钻磨工具串存在多处内外变径。流体流经此类变截面时,因边界的形状发生改变,流线发生弯曲产生旋涡,使流体的流动受到阻碍,如图2所示。此时流体将产生内外局部水力损失hj外和hj内,其计算如下:
(3)
式中:hj外和hj内为外、内局部水力损失,m;λ为局部阻力系数;Q为流体排量,m3/h;As为变径部位环空过流面积,m2;Af为变径部位管内过流面积,m2;g为重力加速度,m/s2。
将钻磨管柱每一内外变径部位取成1个单元,其中钻磨管柱离散成n-1个单元,如图2所示,其中:D1为管柱外扩径单元外径,m;d1为管柱内扩径单元内径,m;D2为管柱外缩径单元外径,m;d2为管柱内缩径单元内径,m。流体的总水力损失hw为:
(4)
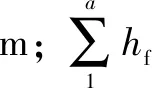
则管壁所受流体的作用合力Fl为:
(5)


图2 管柱变径部位局部水力损失Fig.2 Local hydraulic loss at diameter changing position of string
1.3 钻磨管柱单元载荷分析
1.3.1 直井段管柱单元的载荷分析
在钻磨管柱下钻过程中,直井段管柱单元AB受到流体对称压力、管柱自重、钩载拉力、浮力及内外流体对管壁的作用合力,如图3所示。应用力学平衡原理,建立管柱单元AB在X轴方向的平衡方程为:

图3 直井段管柱单元载荷分析Fig.3 Analysis of string element load in vertical well section
Ti=Ti-1+We-Fl=0
(6)
We=qmkfL
(7)
(8)
式中:kf为浮力系数;ρs为管材密度,kg/m3;Ti,Ti-1分别为管柱单元上下截面所受到的轴向力,N;qm为管柱单元线重,N/m;We为管柱单元浮重,N。
1.3.2 斜井段管柱单元的载荷分析
在斜井段,管柱受井眼轨迹弯曲特性影响,与井筒大面积接触,使得管柱受到较大的弹性摩阻力,管柱发生弯曲[13]。曲率半径R的弯曲应力σf为:
(9)
弯曲应力所产生的附加拉力Fh为:
(10)
式中:σf为管柱曲率半径为R的弯曲应力,MPa;Fh为弯曲应力σf所产生的附加拉力,N;E为管柱材料的弹性模量,Pa;Ah为管柱横截面积,m2。
假设斜井段井眼轨迹中心轴线为一铅垂平面上的曲线,取斜井段的管柱单元CD进行载荷分析,如图4所示。

图4 斜井段管柱单元载荷分析Fig.4 Analysis of string element load in deviated well section
建立受力平衡方程为:
(11)
(12)
(13)
(14)
式中:Mi,Mi-1分别为第i端面和第i-1端面处弯矩,Nm;Qi,Qi-1分别为第i端面和第i-1端面处剪切力,N;μ为单元管柱与井壁的摩擦系数,采用摩擦系数拟合法取值;Ni为单元管柱所受支撑力,N;αi为第i端面处井斜角,(°);Δα为单元管柱两端面井斜角差值,(°);Dw为井筒内径,m;Fih,F(i-1)h分别为第i端面和第i-1端面处附加拉力,N。
通过相关文献[14-16]调研发现,在静流体环境下现有模型对管柱单元的力学分析中,考虑流体作用仅限于竖直方向作用力,而忽略实际流体对管柱单元上下端面无接触,只与管柱侧面有接触,因此采用微元法结合高斯公式的补全法对斜井段和水平段的管柱单元进行受力分析得浮力系数。
斜井段:
(15)
水平段:
(16)
式中:Hm为C端面的垂深,m;kfx为斜井段管柱单元浮力系数;kfs为水平段管柱单元浮力系数。
1.3.3 水平段管柱单元的载荷分析
针对水平段管柱单元载荷分析,做如下假设:1)螺杆前端管柱,考虑管柱做周向转动产生摩阻扭矩;2)螺杆后端管柱,考虑管柱与井筒连续性接触。取螺杆前端管柱单元GH和螺杆后端管柱单元EF进行载荷分析,其中αi=85°~90°,如图5所示。应用力学平衡原理,建立平衡方程为:
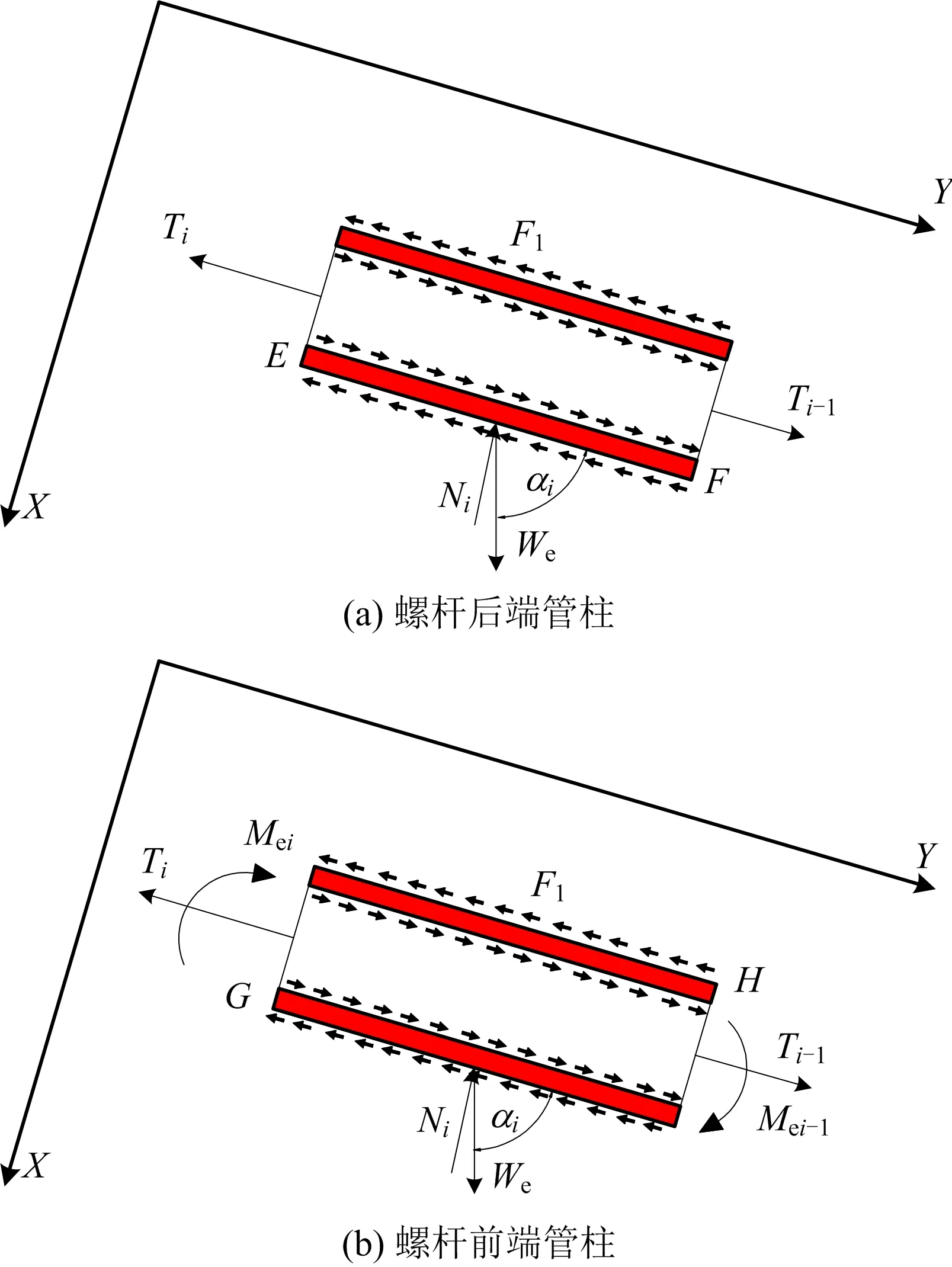
图5 水平井段管柱单元载荷分析Fig.5 Analysis of string element load in horizontal well section
Ti=Ti-1+Wecosαi-μNi-Fl
(17)
Mei=Mei-1+Mz+Mg
(18)
式中:Mz为流体阻力矩,Nm;Mg为管柱惯性扭矩,Nm;Mei,Mei-1分别为第i端面和第i-1端面处扭矩,Nm。
在水平段管柱中,由于磨鞋工具和扶正工具直径最大,导致两者工具间的管柱产生弯曲变形,为研究磨鞋工具与扶正工具之间管柱在井筒中的变形情况,将磨鞋工具及扶正工具视为铰链,取两铰链为管柱单元IJ进行载荷分析,如图6所示。
其中弯矩方程M(y)为:
(19)
管柱单元IJ的弯曲挠曲角为:
(20)
式中:M(y)为管柱单元IJ的弯曲挠曲角,Nm;θi(y)为管柱单元IJ的弯矩,(°);ωi(y)为距I点y处管柱X轴方向产生的挠度,m;αj为y轴与水平面的夹角,(°);Fix为点I受到x方向的支持力,N;Fiy为点I受到Y方向的支持力,N;M1i为点I处管柱的弯矩,Nm;Fjx为点J受到X方向的支持力,N;Fjy为点J受到Y方向的支持力,N;M2j为点J处管柱的弯矩,Nm。
2 实例分析及应用
基于上述模型,开发了钻磨管柱下入性分析软件。该软件能够实现对水平井井身轨迹的绘制、钻磨管柱的组装、钻磨管柱下入载荷的计算;并可通过钻磨管柱通过性分析实现管柱下入安全性分析,软件具体功能及结构如图7所示。
本文以YP10,AP24,AP18,CP13,NP6水平井为例进行分析,其中管柱关键工具参数见表1。
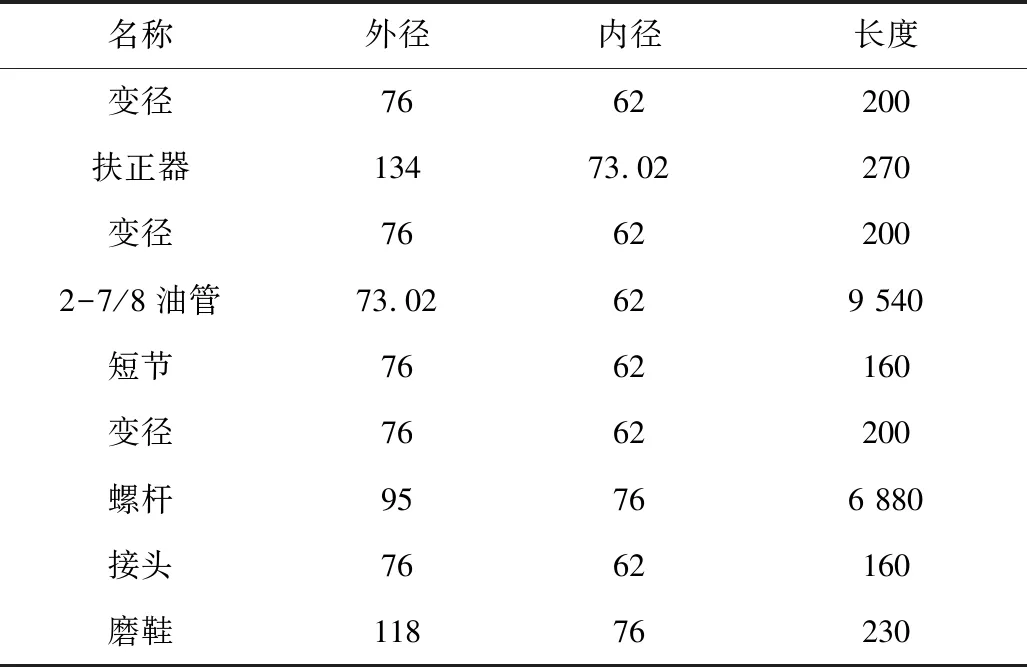
表1 钻磨管柱关键工具参数Table 1 Key tool parameters of drill-grinding string mm
作业基本参数:油管钢级为P110;钻压为12 MPa;井口压力为4 MPa;工作泵压为8 MPa;流体排量为720 L/min;螺杆功率为40 kW;额定扭矩为1 490 N·m。
流体流变参数:流体运动粘度1×10-6m2/s;流体密度为1 000 kg/m3。
基于上述基本参数、流体流变参数和工具参数,通过软件对YP10,AP24,AP18,CP13此4口水平井进行下入载荷分析,计算结果见表2,其中在相同参数下对比实测结果。
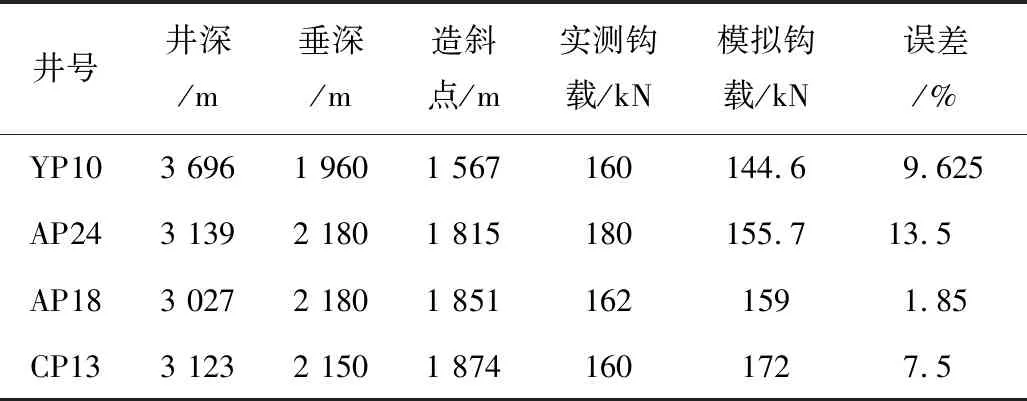
表2 下入钩载的模拟与实测结果对比Table 2 Comparison between simulation results and measured results of tripping hook load
从表2可知,4口井的下入钩载力计算值与实测值的平均误差在8.12%左右,误差在合理范围内,可认为本文研究的下入载荷计算模型与算法合理,能较为准确的进行钻磨管柱的载荷计算,对现场作业起到一定的指导作用,其中误差主要来源于建立的计算模型相比于实际情况进行了简化,其中钻磨作业流体假设为牛顿流体,而AP24误差较大原因是相较于其他实例井,所提供的实测点数据相对较少。
钻磨管柱的关键工具下入至上述4口水平井斜井段的通过性分析数据见表3,通过表3计算结果可知钻磨管柱能安全通过水平井斜井段。

表3 关键工具斜井段通过性分析Table 3 Analysis on passing ability of key tools in deviated well section m
3 钻磨管柱组合特性研究及参数敏感性分析
以AP24水平井为例,选取上述相同的关键工具参数和钻磨作业基本参数,分别对钻磨管柱组合2-7/8单一线重油管、3-1/2单一线重油管和2-7/8油管连接3-1/2油管,其中3-1/2油管长度为1 815 m,进行摩阻力和钩载力计算,计算结果如图8所示。

图8 钻磨管柱下入载荷计算Fig.8 Tripping load calculation of drill-grinding string
由图8可知,连接2-7/8单一线重油管和3-1/2单一线重油管的钻磨管柱达到井底时的钩载力小于采用2种线重油管组合方式的钻磨管柱,通过上述理论分析可知采用油管组合的方式增大了管柱的有效推力,可以提高钻磨管柱的下入能力。
为进一步研究2种线重油管组合方式中大线重油管最优长度大小,根据井眼轨迹依次增加3-1/2油管所占管柱长度进行下入载荷模拟分析,结果如图9所示。

图9 钻磨管柱下入载荷随3-1/2油管占比长度变化Fig.9 Tripping load of drill-grinding string varying with accounted length of 3-1/2 string
由图9可知,随着3-1/2油管所占整个管柱的比例增大,整个钻磨管柱下入到井底位置时的摩阻力和钩载力大小相应增大;当达到斜井段某深度时,钩载力开始减小,对钻磨管柱的下入能力产生阻碍,因此2种线重油管最优组合比例的临界条件在斜井段。
为确定3-1/2油管所占整个钻磨管柱的最优长度大小,为斜井段具体某处井深进行计算分析,结果如图10所示。
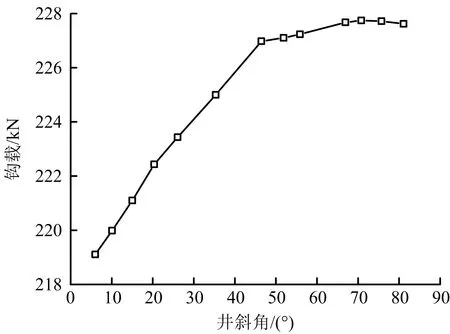
图10 3-1/2油管前端下入到斜井段不同位置时的钻磨管柱井底钩载Fig.10 Well bottom hook load of drill-grinding string when front end of 3-1/2 tubing tripping to different positions of deviated well section
由图10可知,当3-1/2油管长度大小为井斜角70.8°左右的井深时,钻磨管柱下入到井底时的钩载最大,此时组合比例最优,钻磨管柱具有最大下入能力。
在钻磨管柱下入过程中,钻磨管柱除自身的相关参数,还会受到不同摩擦系数的影响。针对不同的摩擦系数,在2-7/8油管连接3-1/2油管的2种线重油管组合方式中依次增加3-1/2油管长度进行钻磨管柱下入载荷计算,结果如图11所示。
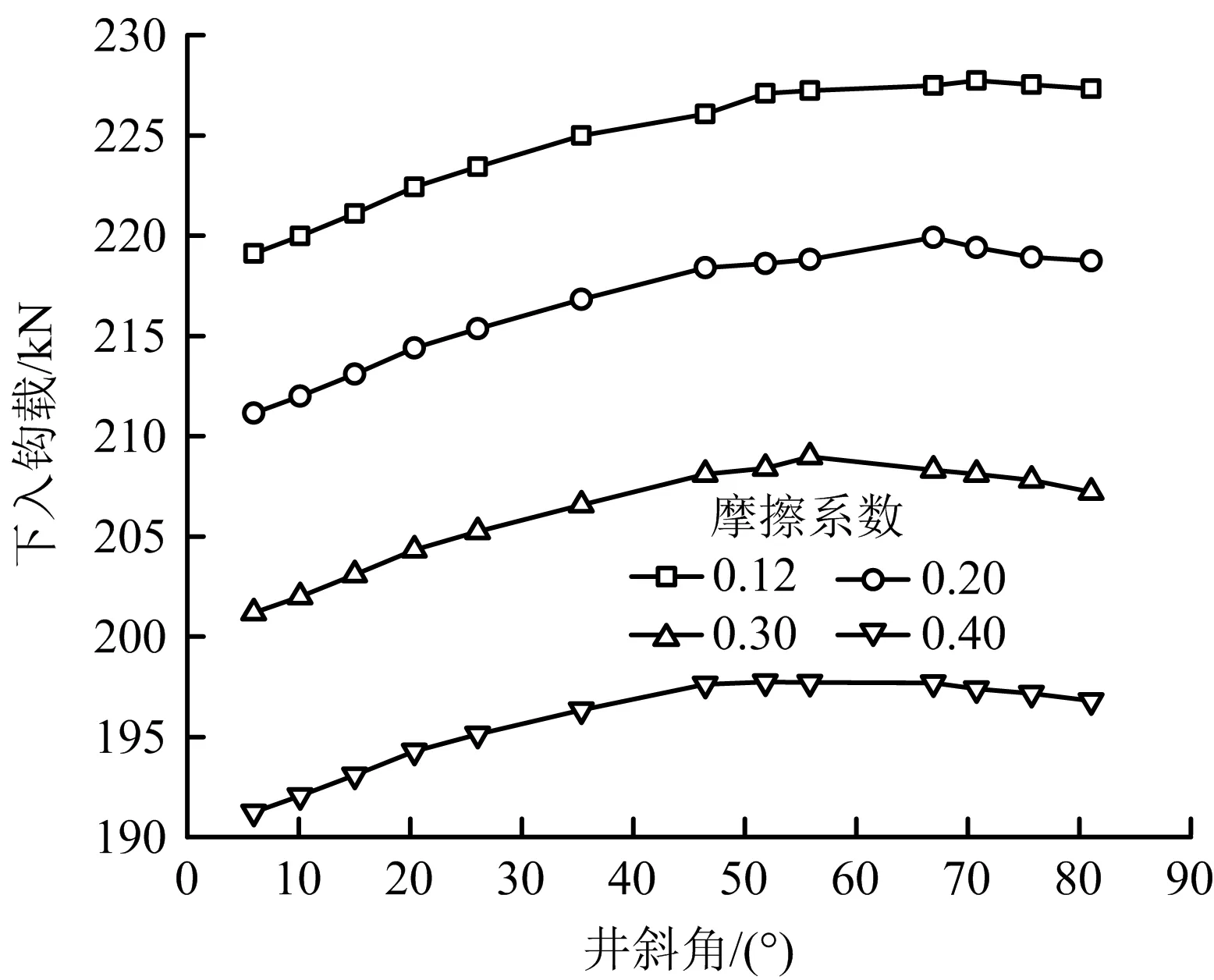
图11 不同摩擦系数对应的3-1/2油管前端下入到斜井段不同位置时的钻磨管柱井底钩载Fig.11 Well bottom hook load of drill-grinding string when front end of 3-1/2 tubing tripping to different positions of deviated well section corresponding to different friction coefficients
由图11可知,不同的摩擦系数μ决定钻磨管柱不同最优组合比例,摩擦系数越大,3-1/2油管所占整个管柱的比例越小。
4 结论
1)根据钻磨管柱存在多变径部位的特点,充分考虑井眼轨迹及管柱内外壁与流体间的相互作用力,采用微元法,建立钻磨管柱的下入载荷计算模型。
2)通过编程进行实例计算,模拟计算结果与实测结果平均误差在8.12%左右,验证了本文建立的计算模型的正确性。
3)采用2种线重油管的组合方式确实能增大钻磨管柱下入能力,当大线重油管所占整个钻磨管柱的长度大小为井斜角70.8°左右的井深时,组合比例最优,不同的摩擦系数μ决定不同最优组合比例,该比例是否适合在其他工况下不同管柱的最优组合,还需结合实测进行进一步研究。
