基于Bezier曲线的特殊螺纹密封面参数化设计*
2019-12-12练章华
张 颖,练章华
(1.四川轻化工大学 过程装备与控制工程四川省高校重点实验室,四川 自贡 643000;2.西南石油大学 油气藏地质及开发工程国家重点实验室,四川 成都 610500)
0 引言
随着我国对天然气资源需求量的不断增加,天然气勘探开发逐渐向深层、超深层发展,井下环境日趋复杂。以塔里木油田为例[1],近5 a油管失效123井次,其中管端接箍开裂、油管断裂占比达43%,造成重大经济损失。管端螺纹的密封性能对井筒完整性和安全性的要求越来越高,常规的API系列螺纹接头已不能满足要求,而特殊螺纹接头在深井、超深气井取得了广泛的关注和应用。
Murtagian等[2]通过物模试验和数值模拟方法研究特殊螺纹密封性能的影响因素,得出特殊螺纹泄漏预测的数学模型和螺纹密封评价准则;Xie等[3-4]建立特殊螺纹金属对金属密封结构的试验模型,研究了密封面长度、油管尺寸、表面粗糙度、螺纹密封脂等因素对密封性能的影响;高连新等[5-6]利用有限元技术和全尺寸试验相结合的方法,研究特殊螺纹接头密封设计的方法,指出密封结构形式的选择与密封面过盈量的确定是特殊螺纹密封设计的关键因素;王建东等[7]采用有限元方法,针对锥面/锥面和球面/锥面2种不同密封结构形式,计算分析了不同载荷工况下螺纹密封面上的接触应力,得出不同密封结构组合下密封能力随载荷的变化规律;张永强等[8]基于圆螺纹设计并加工了1种气密封螺纹结构,接箍中间增加了弹性密封圈,依靠弹性密封圈与套管螺纹的过盈配合实现密封,该气密封螺纹可在鄂尔多斯盆地低压气井、CO2埋存与驱油项目中使用,并能大幅度节约套管成本;张颖等[9-10]建立了特殊螺纹密封面接触应力松弛力学数学模型,以及在微观尺度下建立气体通过金属密封间隙泄漏速率的理论模型,详细分析讨论特殊螺纹的泄漏机制及影响规律;许红林等[11-13]针对特殊螺纹球面对锥面密封结构,建立了考虑密封面作用扭矩的气密封压力计算理论模型,研究了球面半径、锥面锥度等参数对螺纹气密封性能的影响规律。
综上所述,本文提出油套管特殊螺纹密封结构应具有以下特征:曲面对锥面密封,密封接触压力主要源自径向楔紧力,密封接触压力应基本上不受端面轴向扭矩台阶压紧力影响。Bezier曲线具有良好的形状控制能力,在几何造型设计方面有强大的优势,特别是在汽车、航天航空等领域得到了广泛的运用[14-15]。本文在Bezier曲线理论的基础上,提出1套特殊螺纹扣球面对锥面密封结构参数设计的方法,并基于此方法对特殊螺纹密封接头进行优化设计。
1 特殊螺纹密封面结构设计
1.1 Bezier曲线基本理论
1971年法国Renault公司的工程师Bezier提出1种独创的曲线曲面造型方法[16],即由控制多边形来设计曲线。
Bezier曲线的表达式如下:
(1)
式中:Bi,n(t)为 Bernstein基函数;Pi为Bezier曲线的控制顶点。
式(1)为n阶Bezier曲线,将Pi(i=0,1,…,n)顺序首尾连接,从Po到Pn所形成的折线称为控制多边形或者Bezier多边形[17]。其中控制点P0和Pn是Bezier曲线的起始点和终点,其余的控制点通常不在Bezier曲线上。
式(1)中,当n=1时,则表示线性Bezier曲线方程为:
B1(t)=P0+(P1-P0)t=(1-t)P0+tP1,t∈[0,1]
(2)
式(2)等同于线性插值,如图1所示。

图1 线性Bezier曲线Fig.1 Linear Bezier curve
当n=2时,二阶Bezier曲线的表达式如下,
B2(t)=(1-t)2P0+2t(1-t)P1+t2P2,t∈[0,1]
(3)
二阶Bezier曲线由3点构成,其原理是是曲线去逼近控制点P0,P1,P2所构成的三角形,这种曲线能够表达具有一定弧度的形状,如图2所示。

图2 二阶Bezier曲线Fig.2 Second-order Bezier curve
图2中,P0,P1,P2分别是二阶Bezier曲线的控制顶点。Q0在直线段P0P1上变化,从P0移动至P1,Q0的轨迹线描述了一阶线性Bezier曲线;Q1在直线段P1P2上变化,从P1移动至P2,同样,Q1的轨迹线描述了一阶线性Bezier曲线;B点是线段Q0Q1的线性插值点,随Q0和Q1点位置的变化而不断变化,最终形成的路径如图2中曲线所示,该曲线就是二阶Bezier曲线。其中,线段P0P1和P1P2与二阶Bezier曲线保持相切。
当n=3时,三阶Bezier曲线的表达式如下:
(4)
三阶Bezier曲线方程表示了P0,P1,P2和P44个点在平面或在三维空间中定义了三阶Bezier曲线。如图3所示。图3中Q0,Q1和Q2分别在线段P0P1,P1P2和P2P3上移动,其各自的运动轨迹描述了一阶线性Bezier曲线。R0和R1分别为线段Q0Q1和Q1Q2的线性插值点,其各自的运动轨迹线描述了二阶Bezier曲线。B点是线段R0R1所形成线性插值点,其运动轨迹则为三阶Bezier曲线,如图3中曲线所示。其中,线段P0P1和P2P3与三阶Bezier曲线保持相切。
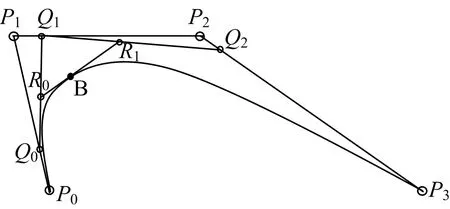
图3 三阶Bezier曲线Fig.3 Third-order Bezier curve
1.2 特殊螺纹密封面结构设计
在工程实践中,常用2次或3次Bezier曲线来满足曲率的连续。针对特殊螺纹扣曲面对锥面密封结构,为了增大特殊螺纹扣密封面接触应力,提高密封接触能,并减小密封接头的塑形变形区域面积,提出采用三阶Bezier曲线作为公接头密封面的曲面方程。基于Bezier曲线公接头密封面结构设计如图4所示。

图4 基于Bezier曲线公接头密封面结构设计Fig.4 Structural design of sealing surface for pin joint based on Bezier curve
根据三阶Bezier曲线方程,首先需要确定4个控制点P0,P1,P2和P3的坐标参数,如图4(b)。结合Bezier曲线起点和终点特性,可以确定图中P0为Bezier曲线的起始坐标点位置,P3为Bezier曲线的终点坐标位置。且规定线段P0P3的水平方向夹角α与母接头密封面内锥角相同。AP3为公接头鼻端止推台肩面,线段AP3与垂直方向夹角为β。
图4(b)为公接头密封面Bezier曲线设计图。根据Bezier理论,控制点P1和P2为自由设计点,由于特殊螺扣止推台肩几何角度和母密封接头几何关系的约束,设计过程中,要求Bezier曲线与公接头止推台阶面AP3相切,即线段P3P2为线段AP3的延长线。且线段P1P2长度为线段P0P3长度的0.3倍。根据平面几何知识,图4(b)中,控制点P2的夹角γ的表达式为:
γ=α-β
(5)
假设控制点P0位置坐标为(0,0),线段P0P3长为l,控制点P1,P2到线段P0P3的高度为h。则得出4个控制点P0,P1,P2和P3的位置坐标分别为(x0,y0),(x1,y1),(x2,y2)和(x3,y3)。
根据图4(b)三阶Bezier曲线控制点几何关系,由解析几何可得:
将式(3)三阶Bezier曲线参数方程展开,可得:
(6)
将控制点P0,P1,P2和P3的坐标带入式(6)即可得到公接头Bezier曲线密封面方程。
Bezier曲线密封面与相同尺寸参数下椭圆曲线密封面的对比如图5所示。其中,Bezier曲线控制参数,l=5 mm,h=1 mm,α=40°,β=15°。从图5中可以看出,Bezier曲线相较与椭圆曲线曲面,在密封接触位置,其曲线凸出更为尖锐,而在非密封接触区域,曲线较为平缓。
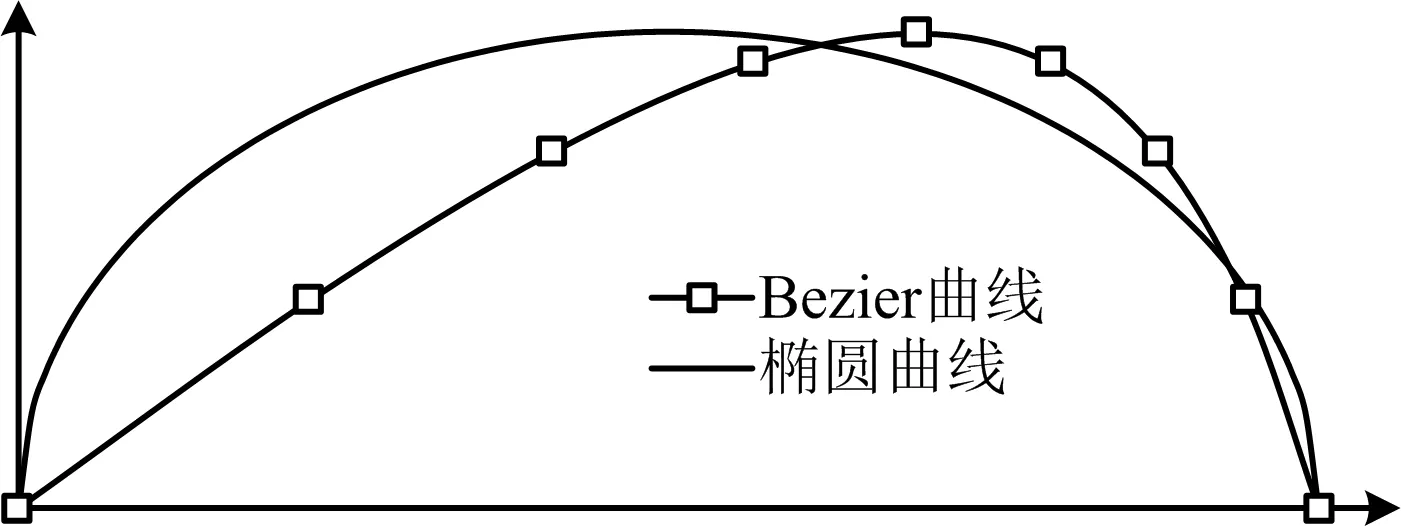
图5 Bezier曲线密封面与椭圆曲线密封面Fig.5 Sealing surfaces of Bezier curve and elliptic curve
2 密封面结构数值仿真研究
2.1 数值仿真模拟
根据Bezier曲线密封面结构设计参数,建立了特殊螺纹扣密封接头的有限元力学模型,如图6所示。由图6可知,公接头密封面采用Bezier曲线密封面,母接头密封面采用锥形密封面,其密封形式属于球面对锥面密封。螺纹接头所用材料为P110T钢级,系各向同性材料,弹性模量为2.10×105MPa,泊松比为0.29,材料的屈服强度为805 MPa。采用127 mm油管,密封接头尺寸基本参数见表1。

图6 基于Bezier曲线设计的特殊螺纹扣密封接头有限元力学模型Fig.6 Finite element mechanical model for sealing joint of premium connection based on Bezier curve design

表1 基于Bezier曲线设计的特殊螺纹扣密封接头基本参数Table 1 Basic parameters for sealing joint of premium connection based on Bezier curve design mm
基于Bezier曲线设计的特殊螺纹扣密封接头Von-Mises应力的分布云图如图7所示,由图7可知,密封接头整体处于弹性变形状态,而在密封面附近出现了塑形变形,其最大Von-Mises应力达到827.4 MPa,说明该密封面已经进入塑形屈服阶段。

图7 基于Bezier曲线设计的特殊螺纹扣密封接头Von-Mises应力分布Fig.7 Distribution of Von-Mises stress in sealing joint of premium connection based on Bezier curve design
基于Bezier曲线设计的特殊螺纹扣密封接头密封面上接触应力分布见图8所示。由图8可知,经过优化设计的特殊螺纹接头密封面最大接触压力达2 060 MPa,密封接触长度为0.6 mm。该密封结构符合金属对金属密封塑形填充要求,在较小的密封接触范围内,产生较大的接触压力。同时,根据金属密封接触能理论,阻止气体通过金属对金属密封结构的流动阻力可由密封接触强度fs表征,它定义为密封接触应力在有效密封长度上的积分值[11]。
(7)
式中:fs为密封接触强度,MPa·mm;L为有效密封接触长度,mm。PsN为密封面上接触应力,MPa。
通过式(7)可以计算出基于Bezier曲线设计的特殊螺纹扣密封接头的密封接触能为821 MPa·mm。

图8 基于Bezier曲线设计的特殊螺纹扣密封接头密封面应力分布Fig.8 Stress distribution on sealing surface for sealing joint of premium connection based on Bezier curve design
2.2 对比分析
将相同尺寸结构的椭圆密封面特殊螺纹扣密封接头与基于Bezier曲线设计的特殊螺纹扣密封接头进行对比分析。其接触面上的Von-Mises应力分布云图以及接触面上的接触应力分布曲线分别如图9~10所示。由图9可知,基于Bezier曲线方程设计的特殊螺纹接头,密封面周围进入塑形区域面积明显减小。塑形区域的减小,可以减小油管接头出现的疲劳破坏,管体裂纹扩展发生的概率。由图10可知,虽然Bezier曲线密封面的密封接触能821 MPa·mm比椭圆曲线密封面的密封接触能905 MPa·mm降低10%,但其密封面的最大接触应力提高了30%,密封接头塑形区域面积减小了40%。因此,该新型密封结构有利于提高特殊螺纹接头的抗疲劳性能,预防特殊螺纹接头应力腐蚀断裂。

图9 密封接触面Von-Mises应力分布Fig.9 Nephogram of Von-Mises stress on sealing contact surface
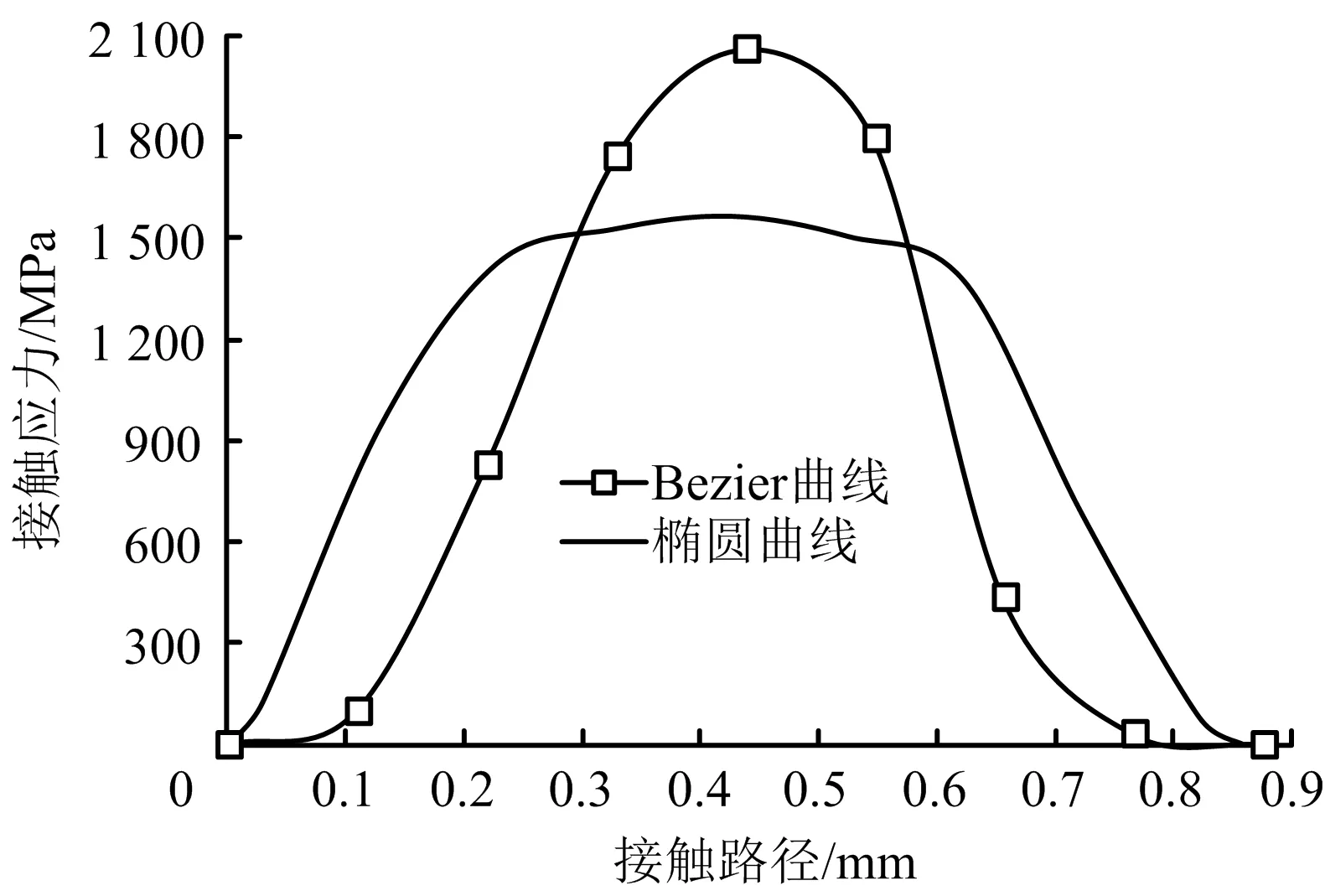
图10 特殊螺纹扣密封接头密封面接触应力分布对比Fig.10 Comparison of contact stress distribution on sealing surface for sealing joint of premium connection
3 结论
1)基于三阶Bezier曲线理论,建立了特殊螺纹密封面球面对锥面密封结构参数化设计模型,通过数值模拟手段,对特殊螺纹密封性能进行系统研究。针对特殊螺纹球面对锥面密封结构,利用Bezier曲线在几何造型的巨大优势,可为特殊螺纹密封面球面设计提供依据。
2)基于Bezier曲线设计的新型特殊螺纹接头密封结构,该螺纹接头提高了密封面接触压力,改善了螺纹接头密封面塑形区域面积,该新型密封结构有利于提高特殊螺纹接头的抗疲劳性能,预防特殊螺纹接头应力腐蚀断裂。
(3)基于Bezier曲线设计的特殊螺纹扣密封接头密封面具有良好的力学性能,可以为深井、超深井油管柱螺纹接头的密封设计提供理论依据。
