不均匀进口总压对涡轮气动性能的影响
2019-12-12史文通伊卫林季路成
史文通,伊卫林,季路成
(北京理工大学机械与车辆学院1,宇航学院2:北京100081)
0 引言
航空发动机/燃气轮机涡轮部件常依据进口参数均匀条件开展气动设计[1-2]。随着涡轮进口温度提高和燃烧室结构复杂化,燃烧室稀释气、冷却气及主流气掺混强烈,导致涡轮进口发生明显的总温畸变、总压畸变及出现旋流现象,但其作用机理及影响规律尚不明晰。真实涡轮进口边界条件对涡轮内流场分布影响研究越来越受到重视。在已有文献中,涡轮进口总温不均匀或热斑相关研究较多,而对于涡轮进口总压不均匀性影响的研究较少[3]。
2000 年和2002 年,Hermanson 与Thole 等[4-5]通过给定涡轮进口流速沿展高方向1 维分布,利用CFD 方法研究了进口总压畸变对涡轮流场通道内影响,发现进口总压分布直接影响涡轮流道内端壁区域的二次流发展;2007 年和2009 年,Barringer 等[6-7]在美国空军实验室涡轮研究平台上,通过调节进口前燃烧室模拟器中的泄漏流和冷却气的温度及流量,创造不同分布形式的涡轮进口边界条件,发现不同进口总压分布可使叶表局部静压负荷发生约10%的变化,同时对叶表靠近端壁区域的换热系数也造成显著影响;2017 年,Wang 等[8-9]通过数值研究指出当有进口总温不均匀性条件存在时,进口总压的不均匀性更直接影响涡轮流道内的热流输运与温度分布。已有的研究表明:涡轮进口总压分布不均匀对涡轮流场内的流动结构和热负荷分布影响值得关注,但进口不均匀分布形式样本往往较少,且进口总压的不均匀性与总温的不均匀性常相互耦合,所得出的结论具有一定局限性。
本文基于数值计算手段,分别以导叶和单级涡轮为研究对象,在总压畸变高度δp和最大总压畸变强度CPmax2 项特征因素的控制下对涡轮进口总压展向1 维分布进行模化,以探究分布特征的变化对导叶及单级涡轮的气动特性影响规律及进口总压畸变环境下涡轮流道内的流动机理。
1 研究对象
本文选定的研究对象为NASA 高效节能发动机计划中的GE-E3 发动机高压涡轮,几何数据来源于文献[2];数值方法校核算例参考试验报告中的无冷却环形叶栅试验对计算域进行构建。数值校验用计算域如图1 所示。进口边界P0的位置参考试验的进口总压测量平面,位于导叶(以下简称NGV)前缘前0.127 m。由于试验的出口静压测量平面P1距离尾缘较近,仅为0.01016 m,为避免由此带来的计算误差,将计算域的出口平面位置向下游充分延长,至尾缘后0.127 m。

图1 数值校验用计算域
对于进口非均匀性对NGV 性能影响,进口边界位置参考文献[10-11]中对于涡轮与燃烧室交接平面(以下简称P40)的定义位置,选定NGV 前缘前40%轴向弦长处为不均匀分布的涡轮进口边界条件的给定位置,相关网格亦做调整,保证不变。其计算域如图2所示。
对于进口非均匀性对单级涡轮性能影响,计算域出口取在动叶尾缘充分距离之后的流道平直段,而出口监测面位于动叶尾缘后0.009525 m。其计算域如图3 所示。
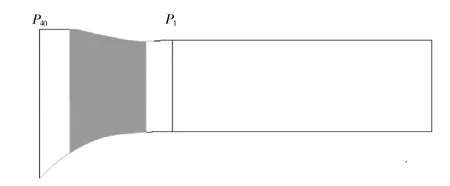
图2 NGV 研究计算域
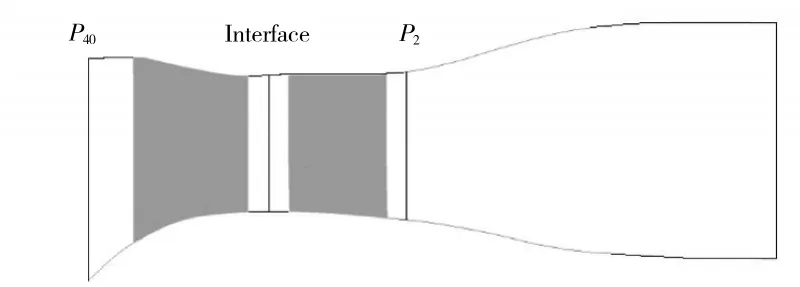
图3 单级研究计算域
在上述2 个方面,对NGV 性能的评估指标采取试验中使用的动能效率ηV,其定义为

式中:V1为出口面P1的实际速度;V1,isen为出口面P1的等熵速度;等效变换后,PS,1为P1面静压;PT,1为P1面总压;PT,0为进口面P0的总压;γ 为比热容比,取1.4。
对1 级涡轮的性能评估指标,采用滞止等熵效率ηst,其定义为
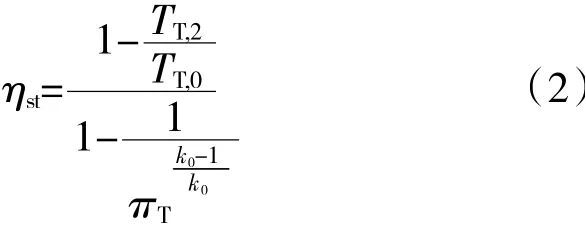
式中:TT,2为P2处的总温;TT,0为P40处的总温;πT为P40面与P2面总压的比值;k0为工质的比热容比,取1.4。
2 研究方法
本文相关工作均基于数值方法开展,网格生成由ICEM 完成,数值模拟利用CFX 进行。首先将结合表1 所示工作条件,针对试验数据进行校核。在计算中,工质选用理想气体,来流方向均匀垂直于进口边界平面且湍流强度为10%[12]。出口给定静压,满足径向平衡方程,参考位置为中展处。在后续研究过程中,除进口总压边界条件外,其余边界条件的给定均与此相同,不再特别介绍。

表1 E3 发动机环形试验边界条件
2.1 网格无关性校验
均保证固壁表面Y+<1,分别生成67、130、192、252 万4 套结构化网格,网格结构如图4 所示。
在校核工况下4 种网格的计算结果见表2。从表中可见,监测参数随着网格总数的增加变化较小,且趋于某一稳定值。
在0%和100%展高位置的绝热Ma 对比如图5所示。从图中可见,随着网格节点总数的增加,叶根和叶顶绝热Ma 分布无明显变化,且都与试验值吻合较好。从上述对比可见,130 万网格可满足网格无关性要求,可用于后续研究工作。
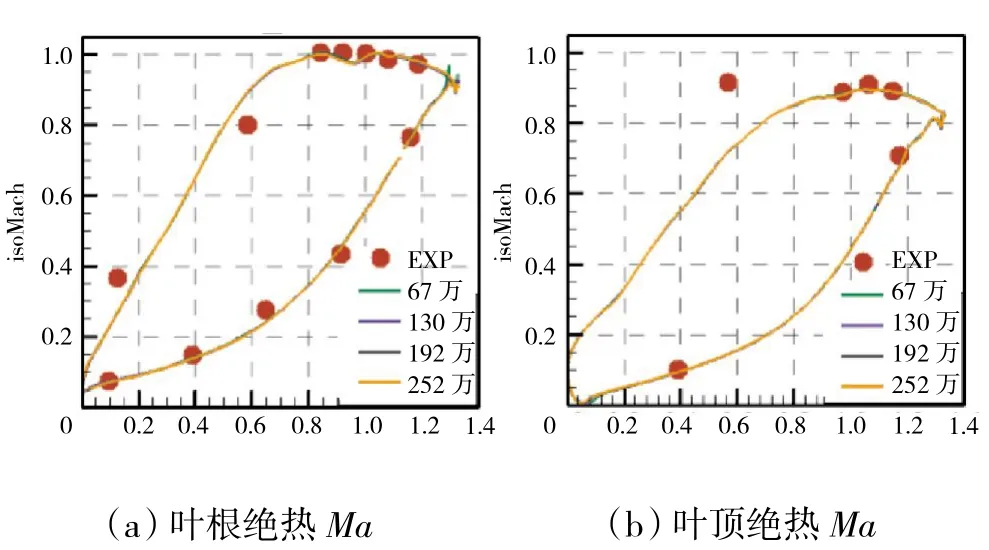
图5 不同网格数下叶根与叶顶绝热Ma 对比
2.2 湍流模型的选择
综合考虑已有校核经验[9,13-14],使用γ-θ 转捩模型应能进一步提高高压涡轮气热模拟的准确性。本文参考试验数据,对比了有/无(γ-θ)转捩模型的SST 湍流模型对NGV“效率-压比”和“流量-压比”的计算差异。
计算结果如图6 所示。当进口总压与出口静压之比发生变化时,SST 模型与SST(γ-θ)模型在出口中展效率ηv和流量2 项计算结果的变化趋势上具有高度的相似性。其中,对于中展效率的预测,当进口总压与出口静压之比小于2.1 时,2 种模型都能较好地预测效率的变化趋势,而数值上SST(γ-θ)模型的计算结果比SST 模型的更接近于试验值;但当进口总压与出口静压之比大于2.1 时,2 种模型都不能非常准确地预测出口中展效率。对于进出口流量的预测,在全压比变化范围内,2 种模型都能较好地模拟流量随压比的变化趋势,且2 种模型计算结果的数值差异不大。对流场进行观测发现,SST(γ-θ)模型对转捩发生的轴向位置的预测比SST 模型的靠后,导致其计算得到的尾迹厚度比SST 模型的薄,因此,其计算得到的中展效率也高。
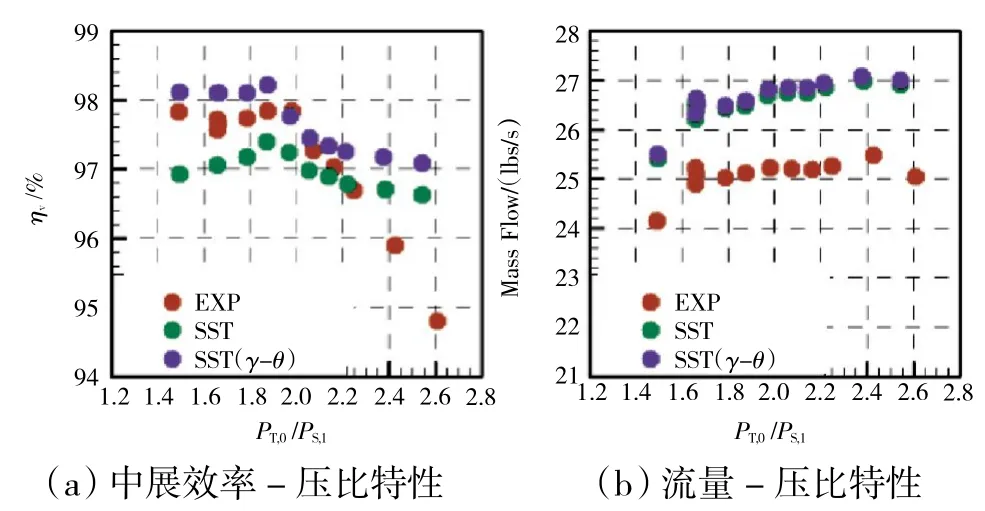
图6 SST 与SST(γ-θ)2 种湍流模型的计算特性对比
出口总效率的预测对比见表3。当进口总压与出口静压之比小于2 时,SST(γ-θ)模型计算结果与试验值相比预测误差更小,考虑到后续研究的展开主要基于设计工况(PT,0/PS,t=1.664),因此,后续的数值计算模型采用SST(γ-θ)模型。
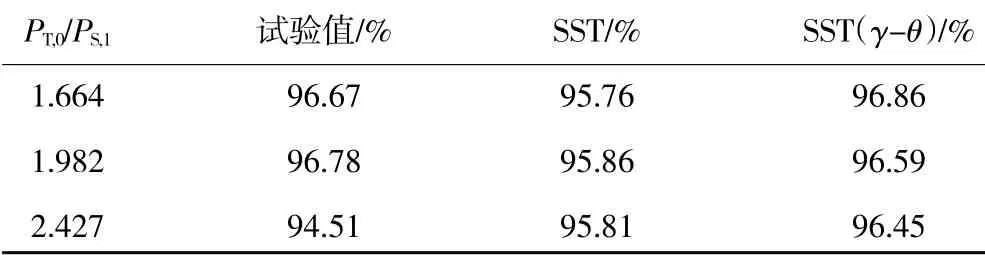
表3 2 种湍流模型在不同压比下出口总效率对比
2.3 进口总压不均匀模化方法
文献[6]给出了发动机真实燃烧室及多种燃烧室模拟器的出口总压沿展高方向分布的试验数据,如图7 所示。从图中可见,总压分布具有靠近中展区域均匀,而在靠近端壁区域从某一展高开始平滑过渡到端壁表面某一极值的特征。
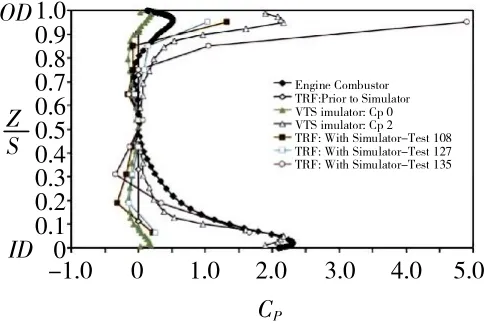
图7 真实燃烧室出口总压分布
因此,本文参考这种分布规律,将其简化为对称分布形式,如图8 所示。从总压畸变发生位置到端壁的总压极值点,使用抛物线公式过渡。在总压畸变高度δP和最大总压畸变强度CPmax2 种变量的控制下,可以获得任意的总压分布。其中,最大总压畸变强度CPmax表示在端区位置处的总压畸变的极值。δP为进口边界总压畸变发生位置距离端壁的距离与进口截面展高的比值。当地总压畸变强度CP用来描述当地总压与中展处总压的差异,即
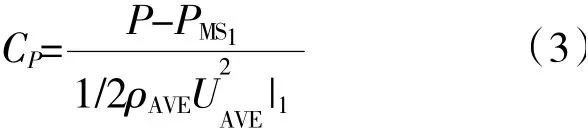
式中:P 为当地总压;PMS1为涡轮进口中展处总压;1/2ρAVEU2AVE|1为均匀进口边界条件下涡轮进口处平均动压。
参考真实情况,本文选定的δP变化范围为[0,40%],CPmax的变化范围为[-2,+2],并分别根据这2种分布特征对NGV 和单级涡轮的气动损失带来的影响进行数值研究。具体方法为,限定δP=30%不变,给定Cpmax={-2,-1.5-1-0.5 0+0.5+1+1.5+2}的进口总压分布条件,以探究总压畸变强度对下游流场的影响;限定|CPmax|=2 不变,给定δP={10%,20%,30%,40%}的进口总压分布条件,以探究总压畸变高度对下游流场的影响。2 个参数变化带来的进口分布变化如图9 所示。
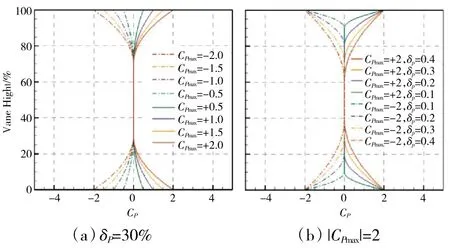
图9 非均匀进口总压分布
3 进口总压不均匀对效率的影响
3.1 NGV效率影响
将如图9 所示的不同进口边界条件施加于如图2 所示的计算域。不同进口条件对于NGV 效率的影响如图10 所示。
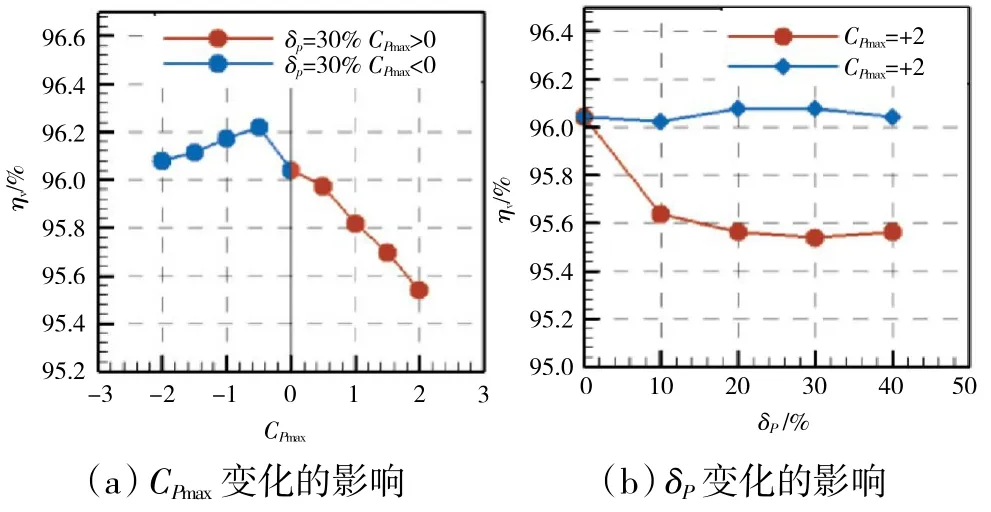
图10 总压畸变对NGV 效率的影响
从图10(a)中可见,当δP相同时,CPmax对ηV有影响,但正/负2 种畸变的影响却不相同。当CPmax>0 时,ηV随CPmax的增大而快速线性降低,影响幅度可达0.5%;当Cpmax<0时,ηV随CPmax绝对值的增大而先快速提高后缓慢降低,但幅度很小,最大影响幅度仅为0.18%。总体来说,当总压畸变为负时,ηV有所提高,但效果不明显;当总压畸变为正时,ηV降低且效果显著,值得进一步深入探讨。
从图10(b)中可见,当CPmax不变时,若CPmax>0,相比于均匀进口总压边界条件,非均匀进口条件会使显著降低,影响幅度可达0.5%。但δP>10%后,随着δP的增大,ηV变化不明显。若CPmax<0,δP的变化对ηV的影响不明显。
在上文各模拟条件中,总压径向分布形式发生了改变,因而总压平均值也发生变化。为了进一步分析是否因进口总压平均值的变化影响ηV,本文还对与各总压畸变情况进口总压流量平均值相同的均匀进口总压边界情况进行计算。结果显示基本无变化,因此,可见ηV的变化主要来自于端区总压变化造成的流道内流场结构改变。
3.2 单级涡轮效率影响
将如图9 所示的不同进口边界条件施加于如图3 所示的计算域。不同进口条件对于单级高压涡轮的滞止等熵效率的影响如图11 所示。
从图中可见,2 种总压畸变特征的变化对涡轮级效率的影响规律与对NGV 的影响规律几乎一致。当CPmax>0 时,CPmax和δP的ηSI变化对的影响幅值分别为0.58%和0.59%;当CPmax<0 时,CPmax和δP的变化对ηSI影响的最大幅值为0.07%和0.06%。
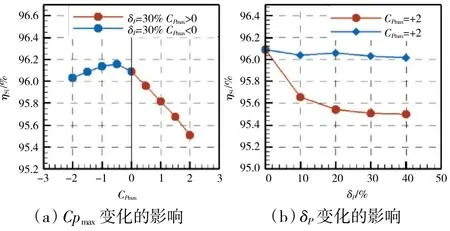
图11 总压畸变对单级效率的影响
同样的,经计算发现,随进口总压分布变化产生的进口总压平均值的变化对于ηSI的影响幅度非常微小,可以忽略不计。
4 内部流场分析
4.1 NGV内流场分析
4.1.1 CPmax>0
P1面经整体流量平均后的NGV 效率沿展高分布如图12 所示。从图中可见,与均匀进口条件相比,当CPmax>0 时,在10%展高以下和80%展高以上的效率有所升高,而在中展区域效率有所降低。并且随CPmax的增大,这一特征越来越明显。
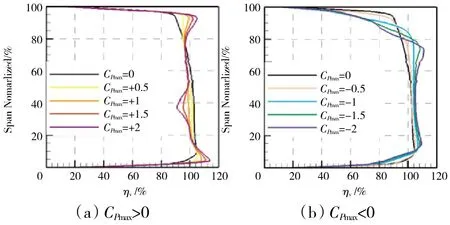
图12 CPmax 对ηV 的影响
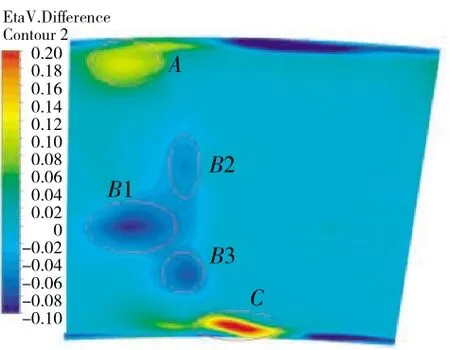
图13 效率监测面上的ηV 分布
选择变化强度最大的CPmax=+2 工况开展进一步研究,将其在P1面上的与均匀进口条件得到的ηV分布进行差运算,如图13所示。从图中可见,2 个高效区A 和C 与1 个大低效区B 的存在,从展向分布上看与图12 的吻合。
对高效区A 的射入流线进行监测,如图14 所示。从图中可见,对于CPmax=+2 的情形,A 区的气体主要由通道中间的气体发展而来,而对于均匀进口条件情形,A 区的气体是流经叶片壁面附近发展而来的。相比之下,在CPmax=+2 时,气体更少流经近壁面区域,也没有发生大的涡流与卷曲,保持了入口处的高总压特征,因此效率更高。

图14 A 区回溯流线
同样的,对高效区C 的流线进行回溯,如图15所示。从图中可见,在均匀进口条件下,C 区的流体曾受到横向二次流的作用撞击到叶片吸力面。而在时,端区流体的总压更高,横向二次流效应减弱,流线未经撞壁,更为平直的射入了C 区,因此损失更小,使C 区的效率更高。
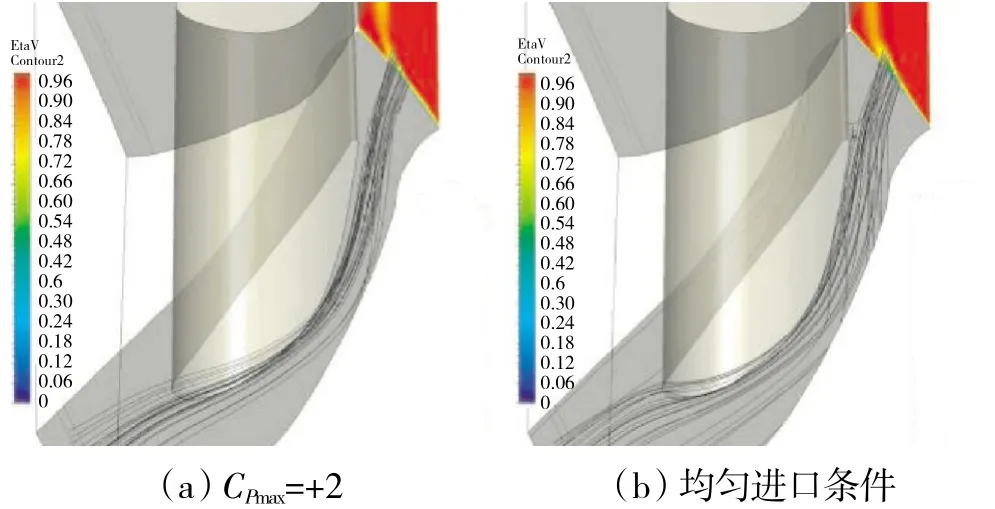
图15 C 区回溯流线
低效区B 由3 个低效核心区B1、B2和B3组成。对这3 个低效区的流线进行回溯发现,B1区的流体主要来自于贴近叶片压力面流动的流体,B2和B3区的流体主要来自于贴近叶片吸力面流动的流体。进口靠近端壁区域的流体受进口总压梯度的作用向中展区域汇集,经过撞击与掺混后流至B1区,而在均匀进口条件下,B1区的流体由进口处同展高的流体平顺发展而来,如图16 所示。从图中可见,流线先通过的云图1 为涡量云图,从该云图中可见,在CPmax=+2 时,端区流体向中心汇聚的过程中产生较强的涡流,由此发生动能损失,使最终汇集到的B1区流体的效率低于均匀进口条件下的效率。
相比于均匀进口条件,在CPmax=+2 时,B2和B3区回溯流体在进口面的展向分布范围更大,如图17 所示。这同样是由于受到端区总压梯度的作用,而使流线向中展区域汇集。

图16 B1 区回溯流线
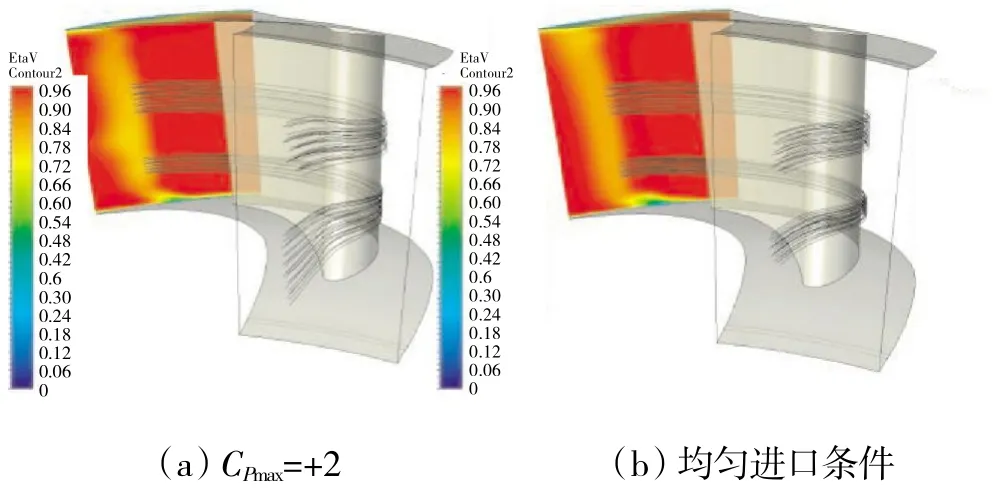
图17 B2 和B3 区回溯流线
但与图16 相比,其汇集作用并没有流经压力面的流体所受到的那样强,流线相对平直,无明显旋流产生,因此,更多的损失应由其他因素造成。B2区所处展高位置约56.5%,绘制该展高位置叶片吸力面上的形状因子分布如图18(a)所示。从图中可见,无论是均匀进口分布还是CPmax=+2 的情况,延流向发展,形状因子都存在由高到低的跳跃过程,通常这一过程由转捩流动导致[15]。但明显可见,在CPmax=+2 时,形状因子跳跃过程发生的位置更加提前,所占轴向距离也更短。说明在CPmax=+2 时,转捩发生得更快且位置更加提前。叶片表面湍动能分布中也能较好地观测到这一现象,如图19 所示。从图18(b)中可见,在CPmax=+2时,转捩后附面层更厚。附面层内流体速度和总压明显低于主流区的,因此当附面层增厚时,尾迹中的高损失区增厚,这也是低效区B2产生的原因。推论低效区B3由同样的理由产生。

图18 吸力面56.5%展高处的形状因子与附面层厚度
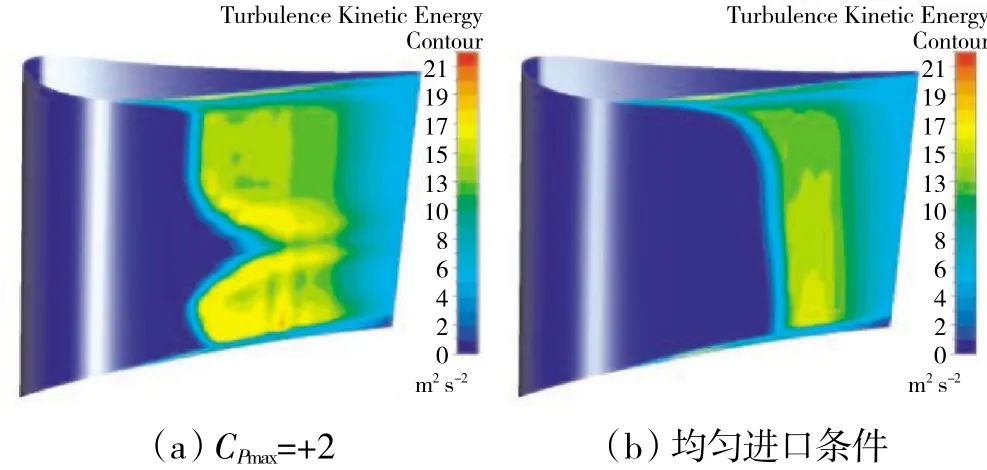
图19 叶片表面湍动能分布
结合图12 与13 可见,在CPmax>0 时,使出口动能效率降低的主要因素是B1区的产生,亦即受进口总压梯度影响的压力面流体向中展区的汇集与碰撞。在δP相同时,CPmax越大,汇集与碰撞的强度越大,因此损失增大,ηV线性降低;而在CPmax相同时,δP越大,汇集点越提前,如图20 所示。但δP足够大时,汇集点进一步提前不能引起汇集点后更多流动形式的改变,因此δP的增大没有使ηV线性降低。
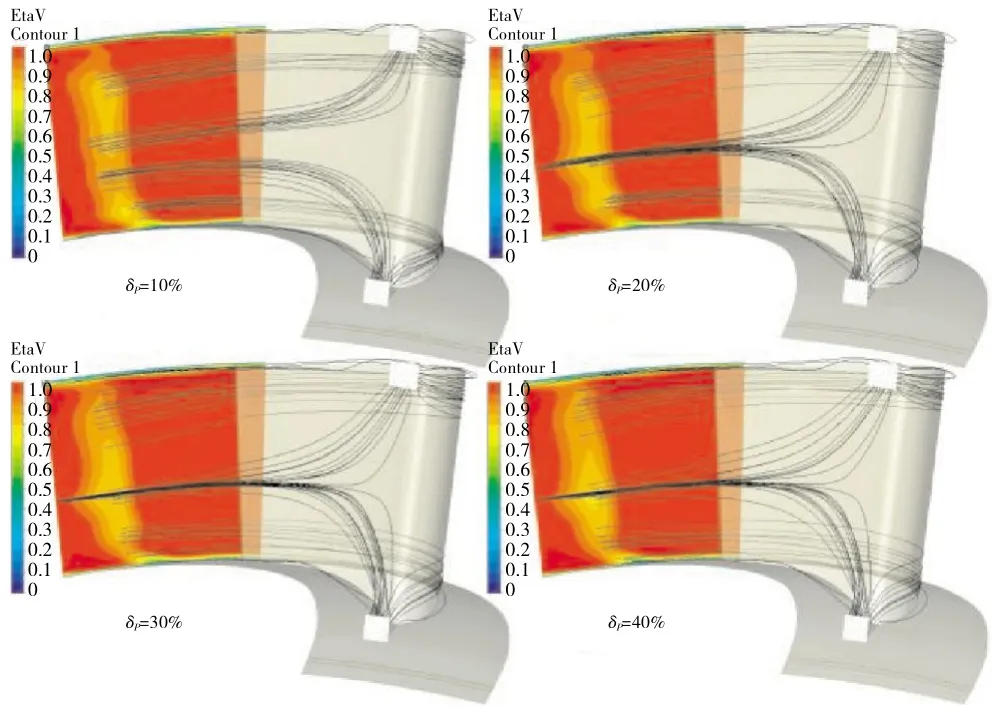
图20 不同δP 情况滞止点前释放的流线(CPmax=+2)
4.1.2 CPmax<0
观察图10 可见,在CPmax<0 时,相比于均匀进口条件,ηV变化不显著,仅略有微量提高。从图12(b)中可见,中展区的整体流量平均效率有明显提高,而端区的效率则明显降低,综合来看整体积分面积变化不大,这与图10 得到的结论是相对应的。为进一步理解其原因,做NGV 效率监测面各展高的流量平均效率分布和流量分布随CPmax的变化曲线,如图21 所示(δP=30%)。从图中可见,在CPmax<0 时,上、下端区各成对出现1 组流量平均效率的高低极值区,但变化幅值较小。从图21(b)可见,与之相比更为显著的,在时,中展区的流量增加,端区流量降低,同时随CPmax绝对值的增大,流量进一步向中展区集中。当取出口面整体流量平均时,在图21(b)中各展高流量的大小相当于图21(a)中各展高流量平均效率的权值,因此尽管端区流量平均效率有所变化,但在CPmax<0 时,对流量分布带来的影响更为显著,中展区域高动能效率流体流量比重的增大,在CPmax<0 时,整体流量平均效率没有降低甚至有微量提高的原因。
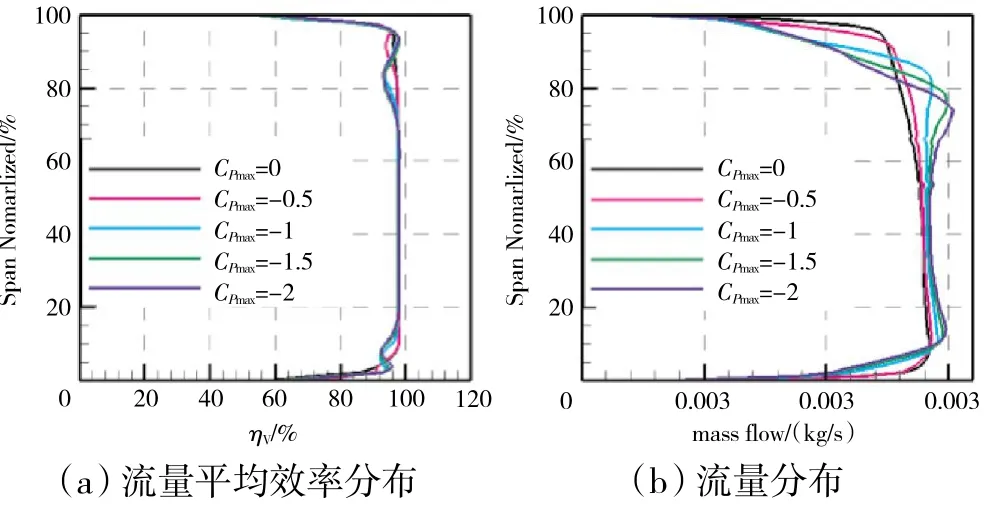
图21 在CPmax<0 时流量平均效率与流量沿展高的分布
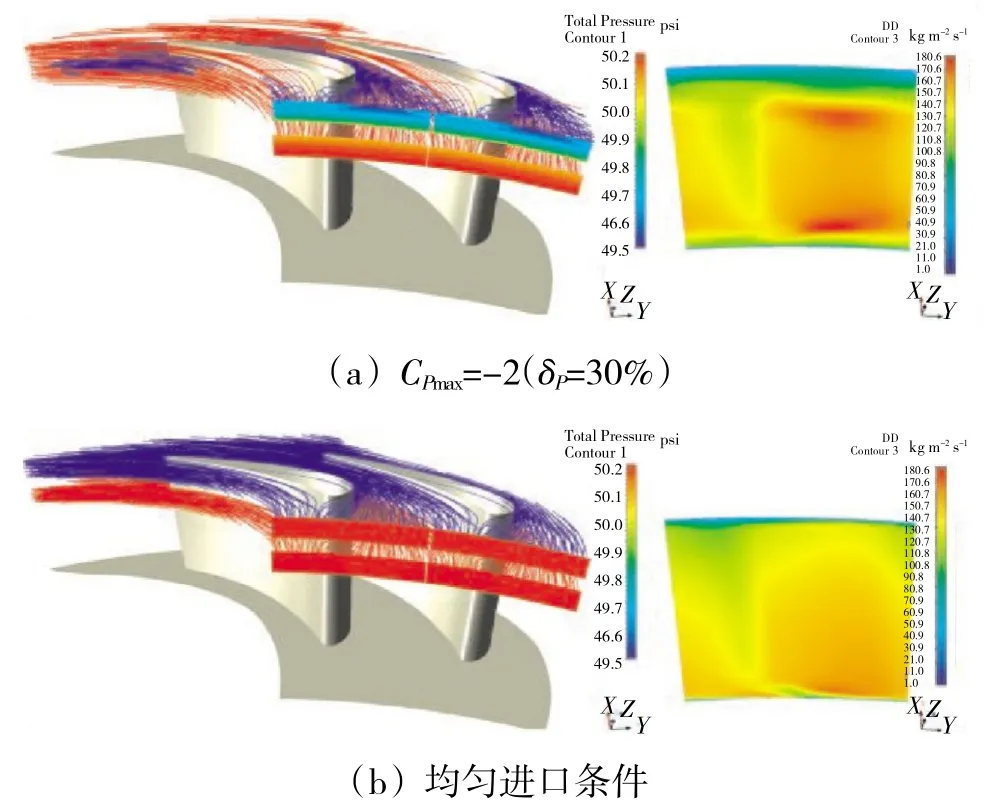
图22 经过P40 面不同展高扇面的流线及P1 面带流量比重的效率分布
在3 维流场中,从进口面90%~100%和70%~80%展高的环形面释放流线,对在CPmax=-2(CP=30%)的情况与均匀进口情况进行观测,如图22(a)所示。其中蓝色流线由90%~100%展高的环面释放,红色流线由70%~80%展高的环面释放。如图22(b)所示的云图为对应情况出口面的ρ*Vw分布,以作为流量分布的参考。对于从2 种不同展高范围出发的流体,都可看作2 部分,一部分的出发位置更靠近吸力面,另一部分则更靠近压力面。在CPmax时,靠近吸力面的流体流速较高,受进口径向总压梯度的作用效果不显著,仍保持较为平直的流线贴近吸力面流动。而靠近压力面的流体流速较低,受到进口径向总压梯度作用后效果显著。对于从进口90%~100%展高出发的流体,其总压较低,在总压梯度作用下向端壁迁∑,撞壁后回流并在靠近进口的区域滚动,最终受横向静压差的作用汇入靠近吸力面流动的高速流体。对于从进口70%~80%展高出发的流体,其总压较高,在总压梯度的作用下,向更高的展高区域流动扩张而未回流,最终占据贴近压力面流动的70%~100%展高的区域,如图23 所示。而这些流体在通过流道时受到横向静压梯度的作用,向吸力面迁∑,并挤占靠近吸立面流动的高展高区域。这部分来自进口靠近压力面位置的流体的流速较低,总压较高,因此最终出口面的高展高区流量减小,原本贴近吸力面高展高区流动的流体被挤压至更低展高区域,使得出口面稍低于机匣的展高区出现了流量汇集。对靠近轮毂的展高区有类似现象,不再赘述。
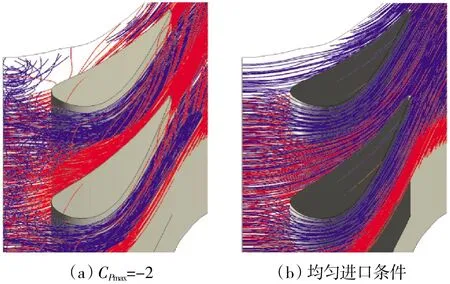
图23 红色流线横向流动,挤占了吸力面高展高区
当δP不变,CPmax绝对值增大时,这种挤占和流量汇集的趋势更加显著,因此出现了如图12(b)所示的出口效率分布变化。而根据图10(b)所示,出口总效率随δP的变化不明显,说明CPmax不变时,δP的变化不会使流动状况发生显著改变,在此不再深入讨论。
4.2 涡轮级内流场分析
4.2.1 CPmax>0
作CPmax=-2(δP=30%)时动叶流道内高损失区的云图,如图25 所示。其中高损失区定义为ΔηSI·ρ·VW<0。从图13 中可见,在CPmax>0 时,静叶出口形成的流体动能损失较高的B,在流入旋转的动叶流道后形成周向全环形的高损失带。又如图24(a)所示,作通过动叶进口高损失带的流线,静叶流道内向中心区汇集的流体在进入动叶流道后以较为平顺的趋势通过了流道。静叶流道出口的流动情况较为平顺地传递到动叶流道出口,因此在CPmax>0时,ηSI随CPmax和δP的变化规律与对静叶流道的相似。

图24 经过中展高损失带的单级内流线
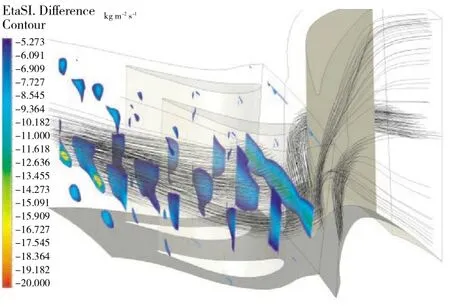
图25 在CPmax=+2 时动叶内流道高损失区的分布
4.2.2 CPmax<0
相似的,做在CPmax=-2(δP=30%)时动叶流道内高损失区的云图,如图26 所示。静叶出口的高损失区在动叶前形成高损失带,其位置集中于上下端壁附近。做通过这2 个高损失带的流线如图27 所示,可见动叶出口的高损失带分布与这些流线在动叶出口通过的位置有对应关系。
因此在CPmax<0 时,ηSI随CPmax和δP的变化规律与静叶流道的相似。
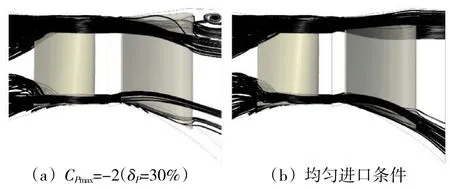
图27 经过端区高损失带的单级内流线
5 结论
本文针对涡轮进口总压沿展高方向1 维分布的不均匀性,利用总压畸变高度δP和最大总压畸变强度CPmax2 项特征因素对其进行模化,开展了不同总压畸变形式对GE-E3 发动机高压涡轮第1 级导叶和第1 级气动性能影响的数值研究,得到以下结论:
(1)当涡轮进口端区总压高于中展区总压时,导叶出口效率显著降低。这主要由靠近压力面流体向中展区的汇集碰撞以及靠近吸力面的流体提前发生转捩流动导致。随畸变强度的增大,导叶出口效率线性降低,幅值可达0.5%。畸变高度的增大,会使汇集位置进一步提前。
(2)当涡轮进口端区总压高于中展区总压时,导叶出口中展区流量增加,端区流量减少,各展高的流量平均效率变化不大,整体平均后,进口总压畸变形式的变化对导叶出口气动效率影响不明显。
(3)从定常解来看,静叶出口的参数分布较为平直地传递到动叶出口,因此,总压畸变对第1 级涡轮气动性能的影响规律与对第1 级导叶的相似。进口总压畸变引发的涡轮级绝热效率降低幅值可达0.59%。
尽管本文所选的型号样本和工况样本具有一定的局限性,但仍可见在涡轮设计过程中,不均匀的进口总压边界条件值得关注和进一步研究。
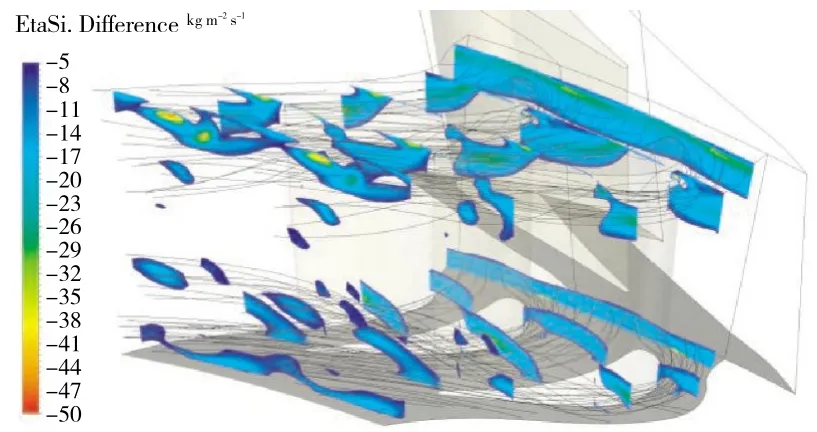
图26 在CPmax=-2 时动叶内流道高损失区的分布
