基于改进的高阶累积量的运动单站高分辨率直接定位方法

吴癸周，张 敏，郭福成，刘章孟

(电子信息系统复杂电磁环境效应国家重点实验室，国防科技大学，湖南 长沙 410073)

0 引言

使用单个运动阵列实现多个窄带辐射源信号的无源定位技术在雷达、通信等诸多领域具有重要的意义。在对辐射源进行无源定位时，往往采用先估计参数，再利用估计的参数进行定位的两步定位法，例如到达角(Angle-of-Arrival, AOA)定位法[1-4]、到达时间(Time-of-Arrival, TOA)[5-8]定位法等。从估计理论的角度看，两步定位法独立地进行参数估计和定位，即使两个步骤都是最优的，但是将两个独立最优的步骤联合起来，估计的结果也有可能偏离最优结果；并且两步定位法还面临参数关联辐射源的问题。

直接定位法(Direct Position Determination, DPD)[9]是一种直接通过阵列天线接收到的原始信号，经过信号处理步骤，得出仅与辐射源位置相关的代价函数，据此实现无源定位的新技术。已有的研究表明[9-16]，DPD具有低信噪比下定位精度更高且可以避免参数关联辐射源的问题等优势。

目前实现DPD的主要方法可以分为2类，一类主要是由Weiss等人提出的基于最大似然准则的直接定位方法[9-11]，该类方法利用最大似然准则推导直接定位的代价函数，通过高维搜索或多次的低维搜索实现多目标的定位；另一类则主要是由OISPUU等人提出的基于子空间的直接定位方法[12-16]，该方法利用类似MUSIC的方法推导直接定位的代价函数，通过低维搜索实现多目标的定位。近年来，Tzafri以及Tirer等人提出了一种基于MVDR的高分辨直接定位方法[17-18]，该方法利用MVDR准则推导直接定位在频域下价函数，通过低维搜索实现多目标的定位，具有分辨率高的优势。在上述方法中，ML需要高维搜索或多次低维搜索，计算量大、复杂度高；基于MVDR直接定位方法与MUSIC类方法分辨率相当。但上述所有基于二阶特性的方法都难以处理辐射源数目大于阵元数目的情况，无法适应复杂的电磁环境。

本文考虑单个运动阵列观测站，被动接受多个窄带辐射源信号，实现直接定位的场景，对此提出了一种基于高阶累积量的高分辨率直接定位方法，同时为了提高分辨率，还使用了基于特征空间的方法对高阶累积量进行了改进。

1 数学模型

考虑这样一个场景。某个均匀圆形阵列，由M个阵元组成，装备于一个运动观测站上，该观测站在累积时间T内在空中飞行，在时刻t(t∈[0,T])时，观测站位置为xo(t)。假设地面上有Q个位于阵列远域的未知位置窄带辐射源同时发射信号，xq为第q个辐射源的位置,如图1所示。

图1 本文所研究的直接定位场景

在此情况下，阵列接收到的信号为：

(1)

式中，s(t,q)为t时刻第q个辐射源的复包络，w(t)为高斯复噪声，a(t,xq)∈CM×1为t时刻第q个辐射源的阵列流形。

将时间T分为N份，每份采样数为K，当N足够大时，可假设在短时间T/N内，阵列流形不变，则式(1)可离散化为：

(2)

式中，wn,k∈CM×1为噪声复包络，k=1，…，K为采样点数。阵列流形可以表示为：

(3)

式中，dm(m=1，…，M)为基于某一阵元，阵列各个阵元的指向矢量，kn(xq)为与辐射源位置有关的参数，其计算公式为：

(4)

式中，λ为辐射源波长，xo,n为第n组数据对应时刻观测站的位置。

式(2)可以进一步简化为：

zn,k=Ansn,k+wn,k

(5)

式中，

(6)

因此，单个运动阵列观测站对多个辐射源定位的数学模型为：

Zn=AnSn+wn

(7)

式中，

(8)

从式(7)可知，单个运动阵列观测站对多个辐射源的直接定位问题即为通过式(7)求解xq的问题。

2 定位方法

利用式(7)直接估计多个辐射源的位置，实际上是一个非线性寻优的问题，可以通过类MUSIC等方法给出代价函数，然后进行可行域内的搜索实现定位。但是由于考虑辐射源数目大于或等于阵元数目的情况，而类MUSIC等利用二阶特性的方法将无法使用，因此考虑可以拓展阵列的高阶统计量[19]方法。其中四阶累积量具有自动抑制加性高斯白噪声及任意高斯色噪声的能力[20]，因此本节以四阶累积量为例给出了相应的代价函数。同时，由于辐射源数目多，对定位分辨率也提出了较高的要求，采用基于特征空间的方法[21]实现高分辨率的四阶累积量直接定位方法。

2.1 基于四阶累积量的类MUSIC的DPD

对于零均值平稳随机过程，四阶累积量有多种定义，以下式为例：

(9)

式中，(·)*表示取共轭，zn,m1表示阵列第m1个阵元接收到的第n组数据，而式(9)中的计算目前普遍用下式替代：

(10)

式(9)、(10)中变量的取值范围为1≤m1,m2,m3,m4≤M，则随着m1,m2,m3,m4的变化，共有M4个值，这些值可以构成一个M2×M2的矩阵R4,n:

R4,n((m1-1)M+m3,(m2-1)M+m4)=C4x,n(m1,

m2,m3,m4)

(11)

进一步化简式(11)，有：

(12)

式中，⊗表示克罗内克积，且有：

(13)

Bn可以视为四阶累积量下的阵列流形。由文献[20]可知，对于上述构造的四阶累积量，如果采用均匀圆阵，则拓展后的阵元数为M2-M+1。因此，当辐射源数Q≤M2-M+1时，Bn列满秩，可以直接将MUSIC方法推广。

(14)

则推广的MUSIC的代价函数为：

(15)

2.2 基于四阶累积量的特征空间DPD

在文献[21]中提出了一种基于特征空间的直接定位方法，该方法分辨率要高于MUSIC类直接定位方法，下面给出其在四阶累积量上的推广形式。

(16)

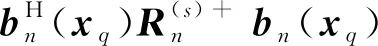
=1/pn,q

(17)

式中，(·)+表示求矩阵的广义逆，δxq=[0,…,1,0,…,0]T，表示第q个元素为1，其余元素为0的Q×1矢量，pq表示第q个辐射源在第n组时间内辐射的能量。

定义一种新的空间谱函数:

(18)

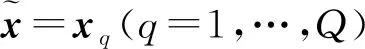
3 仿真分析

定义如下仿真场景，观测站在空中由[0 0.5 0.5] km匀速直线飞行至[0 -0.5 0.5] km，总观测时间为T=12 s，观测站上装有M=5阵元均匀圆阵，圆阵半径设为λ/(2sin(π/2M))，λ为波长，每1 s分为一组，每组采样1000个点，采样频率为1 GHz；地面有5个辐射源同时发射窄带信号，设定各个辐射源信号互不相关，位置分别为[-0.3 0 0],[0 0 0],[0.3 0 0],[0 0.3 0],[0 -0.3 0] km。则可行解空间及阵列运行轨迹在其上的投影如图2所示。

图2 5个辐射源的定位场景

设定信噪比为30 dB，分别利用式(15)、(18)计算四阶累积量DPD(DPD-HOC)和改进四阶累积量DPD(DPD-HOC-ES)的空间谱函数并与最大似然DPD(DPD-SML)[22]相比较，则得到的空间谱如图3～5所示。

从图3～5不难看出，在辐射源数大于或等于阵元数时，DPD-HOC和DPD-HOC-ES两种方法都可以在辐射源真实位置处形成明显的谱峰，并且DPD-HOC-ES的谱峰更加集中，其分辨率要优于DPD-HOC，但是DPD-SML方法虽然也可以形成相应谱峰，但是其空间谱模糊，分辨率很低。

图3 SML谱图

图4 DPD-Hoc谱图

图5 DPD-Hoc-ES谱

为了进一步研究该算法在定位分辨率上的优势，设定如下场景，地面有2个辐射源同时发射窄带信号，设定各个辐射源信号互不相关，位置分别为[-0.1 0 0],[0 0 0]km，其余条件保持不变，则可行解空间及阵列在其上的投影如图6所示。

图6 2个辐射源定位场景

设定蒙特卡洛仿真次数为1000次，以emitter2为例统计其随信噪比变化的定位均方根误差(RMSE)，结果如图7所示。

图7 辐射源2定位性能示意图

从图7可以看出，DPD-HOC和DPD-HOC-ES的方法可以准确对emitter2进行定位，并且DPD-HOC-ES的定位精度高于DPD-HOC，说明其分辨率更高。另外，当信噪比大于-5 dB时，DPD-HOC-ES和DPD-HOC的定位精度随信噪比的增加不再有明显的变化，说明基于HOC的直接定位方法对高斯噪声具有较好的抑制作用。而DPD-SML由于分辨率低，无论在高信噪比还是低信噪比下都无法将这两个临近目标区分开，因此其定位误差也一直较大。

4 结束语

本文提出了一种基于四阶累积量的直接定位方法，该方法可以对大于或等于阵元数的辐射源进行直接定位，为了进一步提高分辨率，本文借用特征空间的方法对其进行了优化，仿真表明了该方法对大量辐射源(辐射源数目等于阵元数)具有准确的定位能力。但是该方法也具有运算量大的缺陷。因此，克服这一困难的大量辐射源直接定位法是以后的研究重点。