基于深度卷积网络的PRI调制模式识别方法

茆旋宇，郑子扬，王 佩，郭 涛，鲁加战，卢志龙，祁友杰

(中国航天科工集团8511研究所，江苏 南京 210007)

0 引言

现代战争中大量复杂体制雷达广泛应用，雷达信号的脉冲重复间隔(PRI)调制模式识别是雷达告警接收机(RWR)和电子支援(ESM)系统中进行辐射源识别的关键组成部分，它为型号识别、类型判决、工作模式识别和威胁评估，以及构建辐射源识别数据库提供数据支撑，也为电磁环境态势感知和干扰样式决策的提供重要依据。随着新体制雷达迅猛发展并获得广泛应用，雷达采用的PRI调制模式也变得日益复杂，主要包括：参差、抖动、驻留与切换、滑变、正弦，以及滑变和参差的复合调制等。这些复杂调制样式给雷达信号PRI调制模式识别技术带来了更加艰巨的挑战。

现有的复杂PRI调制模式识别方法大致可以分为2类。第1类是基于特征提取与门限判决的识别方法。文献[1]提出了PRI调制样式的识别算法与实现流程，实现了5种典型PRI调制样式的有效识别，该方法在PRI测量精度较低和丢失虚假脉冲比例较高的情况下具有稳健的识别性能。文献[2]在分析PRI序列的时域及频域特性的基础上，定义了零交叉密度、谐波幅度比、PRI序列差分极性3个分类特征，特征提取方法简单且可在小样本条件下实现。文献[3]通过提取PRI序列的极值特征，构建极值序列特征集来进行调制模式识别；基于特征的分析和提取，通过设定特征参数门限的方法，实现PRI调制模式在特征空间的分类和识别，但该类方法的识别有效性严重依赖于门限选取，门限的有效性直接影响了识别效果。

第2类是基于提取的特征参数进行有监督分类或无监督聚类的识别方法。文献[4～5]提出了新的特征矢量提取方法，并引用神经网络进行识别。还有文献[6]提出了一组二维特征向量，采用支撑向量机SVM分类器进行识别。文献[7]提取了几种PRI序列特征量，通过贝叶斯多网络分类器的概率推理能力来实现雷达重频模式识别。此类识别方法依赖于事先准确提取的精细特征或多维特征的组合，而对不同调制模式提取特征的有效性直接影响了识别准确率。

本文提出了一种基于深度卷积网络的PRI调制模式识别方法，利用数据驱动的思想，在不事先刻意提取物理含义特征的前提下，针对包含PRI复合调制在内的8种复杂调制模式，进行了调制模式的有效识别。仿真表明，本文方法在存在干扰脉冲率高、脉冲丢失严重、测量噪声大，以及小样本脉冲的电磁环境中能够保持良好的识别性能。

1 PRI调制类型与特性分析

雷达在执行不同的任务时，往往会采用不同的PRI调制模式，而雷达发射脉冲信号的时间间隔则是PRI调制的具体表现。被动接收机要截获和识别脉冲信号的PRI序列，需通过测量脉冲到达时间(TOA)来获得，如下所示：

f(k)=Tt(k+1)-Tt(k)

(1)

Tr(k)=Tt(k)+Tl(k)

(2)

(3)

目前复杂PRI调制模式通常分为参差、抖动、滑变、正弦、参差与滑变复合等几种调制模式。

1.1 参差调制

参差调制模式的PRI序列值是在一定范围内，按照若干个固定值的排列顺序进行周期性重复，其单个周期的PRI序列描述模型为：

(4)

式中，Pk为单周期序列内的第k个PRI值，M为PRI值的总数，骨架周期PF为：

(5)

1.2 抖动调制

抖动调制模式的PRI序列值是在一定范围内，围绕某一个中心值附近抖动，其描述模型为：

f(k)=PJIT+v(k),k=1,2,…,N

(6)

式中，PJIT为抖动中心值，v(k)为抖动量，N为PRI值序列长度。

1.3 驻留与切换调制

驻留与切换调制有时也称为成组参差或成组跳变，PRI值采用2个或2个以上的脉冲重复周期，通过顺序、重复地利用脉冲重复周期序列集合中的PRI值产生脉冲序列。一个长度为L的单周期N重频驻留与切换调制的描述模型为：

(7)

1.4 滑变调制

滑变调制模式的PRI序列变化规律为单调递增或递减，其滑变调制的描述模型分别为：

f(k)=Pu+Suk,k=0,1,…,Lu-1

(8)

f(k)=Pd-Sdk,k=0,1,…,Ld-1

(9)

式中，Pu、Su和Lu分别为递增滑变的最小值、速率和序列长度。Pd、Sd和Ld分别为递减滑变最大值、速率和序列长度。

双滑变调制是递增和递减两个滑变调制的复合，一个先增后减的单周期双滑变调制描述模型为：

(10)

式中，L=Lu+Ld为单周期PRI序列的总长度。

1.5 正弦调制

正弦调制的PRI序列近似满足正弦或余弦函数变化规律，其描述模型为：

f(k)=PWOB+PW/2+PW/2cos(ωk)

(11)

式中，PWOB是最小值，PW是幅度的最大值与最小值的差(即振幅值)，ω是角频率。

1.6 参差与滑变复合调制

参差与滑变复合调制的PRI序列在一定范围内既具有参差特征，又具有滑变特征。单周期的2参差递增滑变描述模型为：

(12)

式中，R1={1,3,…,L-1}，R2={2,4,…,L}，Pu1和Pu2分别为2个PRI递增起始值，Su1和Su2分别为2个PRI滑变递增速率，通常Su1=Su2，单周期PRI序列的总长度L为大于0的偶数，mod(·)为模运算。一个单周期长度的2参差递增滑变描述模型为：

f(k)=

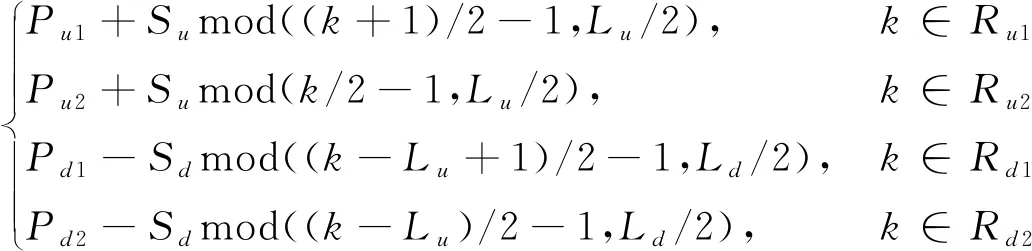
(13)

式中，Ru1={1,3,…,Lu-1}，Ru2={2,4,…,Lu}，Rd1={Lu+1,Lu+3,…,Lu+Ld-1}，Rd2={Lu+2,Lu+4,…,Lu+Ld}，Pu1、Pu2和Pd1、Pd2分别为2个PRI递增起始值和2个递减起始值，Su和Sd分别为PRI滑变递增速率和递减速率，一般情况下递增速率等于递减速率，Lu和Ld分别为单周期递增和递减序列的长度，均为大于0的偶数。

8种调制模式的PRI序列特性如图1所示。

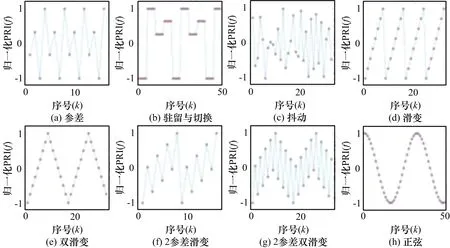
图1 8种PRI调制模式序列特性

2 基于卷积网络的PRI调制模式识别

卷积神经网络具有实现简单，对非结构化数据特征提取能力出色等优点，被广泛应用于计算机视觉、语音识别等领域。其组成可分为卷积层、池化层和全连接层，基本结构由图2所示。

图2 卷积神经网络基本结构

2.1 算法与实现架构

算法基本原理如图3所示，首先将采集数据进行数据预处理和调制模式标注，分别生成训练数据集和测试数据集。其次构建卷积神经网络，使用训练数据集进行训练，得到训练好的模型。最后使用该模型对不同实验场景下的测试数据集进行推理识别，分析网络模型的识别性能。

图3 PRI调制模式识别架构框图

其中，采集数据为PRI序列，通过预处理对数据进行标准化便于网络训练，使用独热编码对不同调制模式的数据进行调制类型标注。

根据输入数据的特点，构建基于VGG结构的卷积神经网络。VGG网络是一种经典的卷积神经网络，通过堆叠多个小卷积核在不增大模型参数的情况下大大提升了网络性能[8]。此外，还借鉴一些新模型的思想，舍弃全连接层，使用GlobalAveragePooling层代替[9]，网络结构如表1所示。

卷积层主要用于“空间滤波”，通过构造卷积核，以滑动窗口形式对输入进行加权计算，起到提取输入特征的作用。实现原理为：

(14)

式中，yi,j为输出在第i行j列上的结果，ωm,n为卷积核在第m行n列上的权重，k,j表示卷积核的尺寸，xi-m+1,j-n+1为输入数据对应位置的值。

表1 网络结构

BatchNormalization层对输入数据的分布做归一化处理，使得输入分布更加均匀和固定[10]，加速网络收敛。其数学表达式为：

(15)

(16)

Y=γ*(X-μ)/(σ2+ε)1/2+β

(17)

式中，X为上一层的输出，xi为其第i个节点的值，μ和σ2为其均值和方差，ε为一很小的正数防止σ2为0，Y为输出结果，线性运算的权重γ和β通过训练得到。激活层使用relu，其实现简单，权值梯度不易饱和，反向求导速度快。

GlobalAveragePooling通过对卷积层输出的每一个feature map进行全局平均达到降低网络参数同时保留空间信息的目的[11]，用于替代全连接层。Softmax函数通过对各个神经元输出指数运算的结果进行归一化，令输出结果之和为1，从而使输出结果表示各个类别的分类概率，用于解决多分类问题，其数学表达式为：

(18)

式中，xi为上一层第i个神经元的输出。

2.2 网络训练

选用交叉熵作为损失函数，其数学表达式为：

(19)

式中，a为Softmax的输出结果，y为真实标签值，已转化为独热编码，i代表输出节点号。

优化器选择Adam，使用变化学习率训练网络。

识别效果的单一评价指标选用F1-score，等价于精确率和召回率的调和平均值，数学表达式为：

(20)

3 仿真实验与分析

为了验证本文提出方法的有效性，在含有干扰脉冲和脉冲丢失的环境下，以及不同测量噪声和小样本环境下，对本文涉及的8种雷达PRI调制模式信号进行识别，由于篇幅的限制只列出了与该算法有关的主要参数，如表2所示。

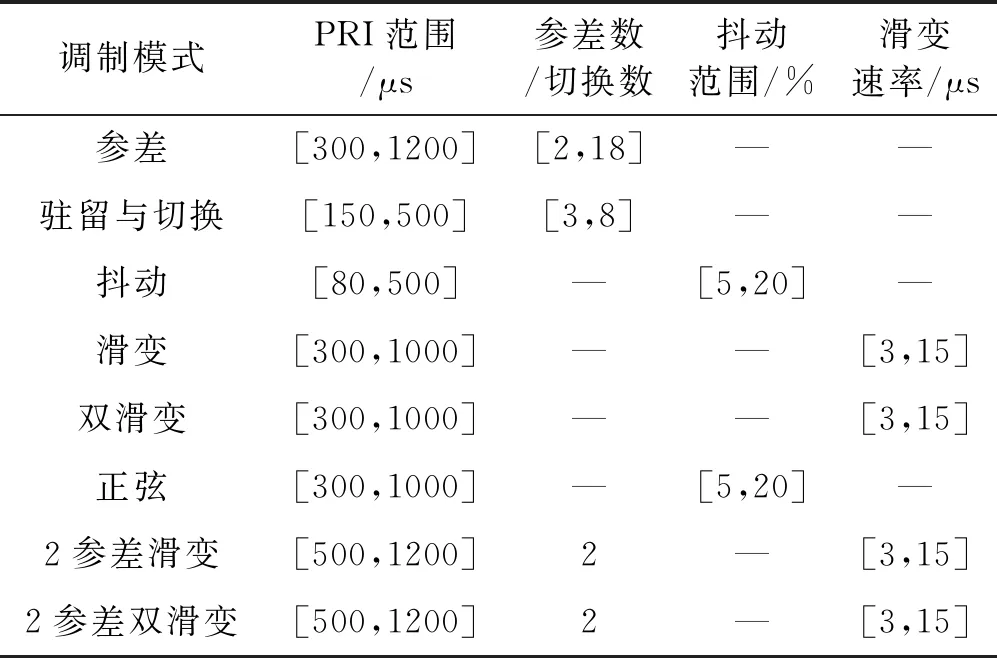
表2 8种PRI调制模式参数

首先构建训练数据集训练卷积神经网络，训练数据由多种不同干扰率、丢失率、测量噪声影响的数据组成，具体组成分布由表3所示。每种调制模式分别由2%～24%干扰率、2%～24%丢失率和40～480 ns的测量噪声下的样本组成，每个样本包含长度为128的PRI序列，每种模式生成5万条样本，训练数据集共计40万条样本。使用该训练数据集对卷积神经网络训练，设定初始学习率为0.01，batch size为256，迭代周期为20，得到最终的网络模型。

表3 训练集组成

3.1 干扰脉冲实验

在真实的复杂电磁环境下，接收机性能或使用方式的不同，会不可避免地导致信号分选后的雷达脉冲流中掺杂着干扰脉冲。而干扰脉冲的存在也影响着PRI调制模式的识别准确率。

在上述仿真环境中，对每一串脉冲样本增加脉冲总数量2%～50%的随机干扰脉冲，每个样本包含的PRI序列长度为128，不同干扰率下每种调制模式仿真了1万条样本作为测试数据。使用已训练好的模型，分别去识别不同干扰率的样本数据，各PRI调制模式在不同干扰率下的识别准确率如图4所示。

图4 干扰脉冲环境下PRI调制模式识别率

从图4可以看出，当干扰率不超过32%时，各种调制模式的识别率均在95%以上，模型具有较好的识别性能。干扰率达到40%时，模型的平均识别率仍能保持在80%以上。干扰率继续提高，识别性能开始不断恶化，这主要是由于测试数据与训练数据差异过大，模型无法有效地对测试数据进行泛化。因此在实际使用中，训练数据需要尽可能涵盖各种可能的情况。

3.2 丢失脉冲实验

由于接收机和雷达波束在空间中的方位关系、接收机处理同时到达信号的体制和方法，以及信号分选产生的误差，分选得到的脉冲流总会存在脉冲丢失的情况，而这也会对识别准确率产生影响。为验证丢失脉冲对模型识别性能的影响，随机丢失每一串脉冲样本总数2%～50%的脉冲，每个样本包含的PRI序列长度为128，样本数量与干扰脉冲实验相同。最终得到识别结果如图5所示。

由图5可知，随着脉冲丢失率比重的增大，识别准确率在逐渐下降。当丢失率不超过30%时，平均识别率在95%以上。当丢失率超过32%时，模型识别率下降。尤其是参差和正弦调制两种模式，这主要是由于因为训练数据覆盖的丢失率范围较小，测试数据的丢失率远大于训练数据的丢失率，模型的泛化能力不足。

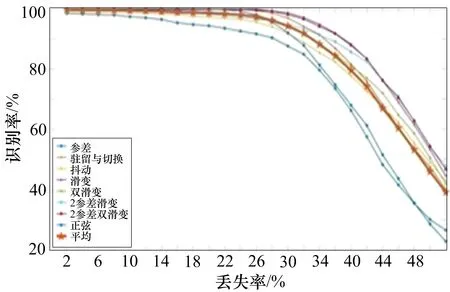
图5 脉冲丢失环境下PRI调制模式识别率

3.3 测量噪声实验

实际场景下，接收信号还会受到测量噪声的影响，为了验证模型的抗测量噪声性能，对每一串脉冲样本增加40～1000 ns的随机Toa测量噪声，识别结果如图6所示。

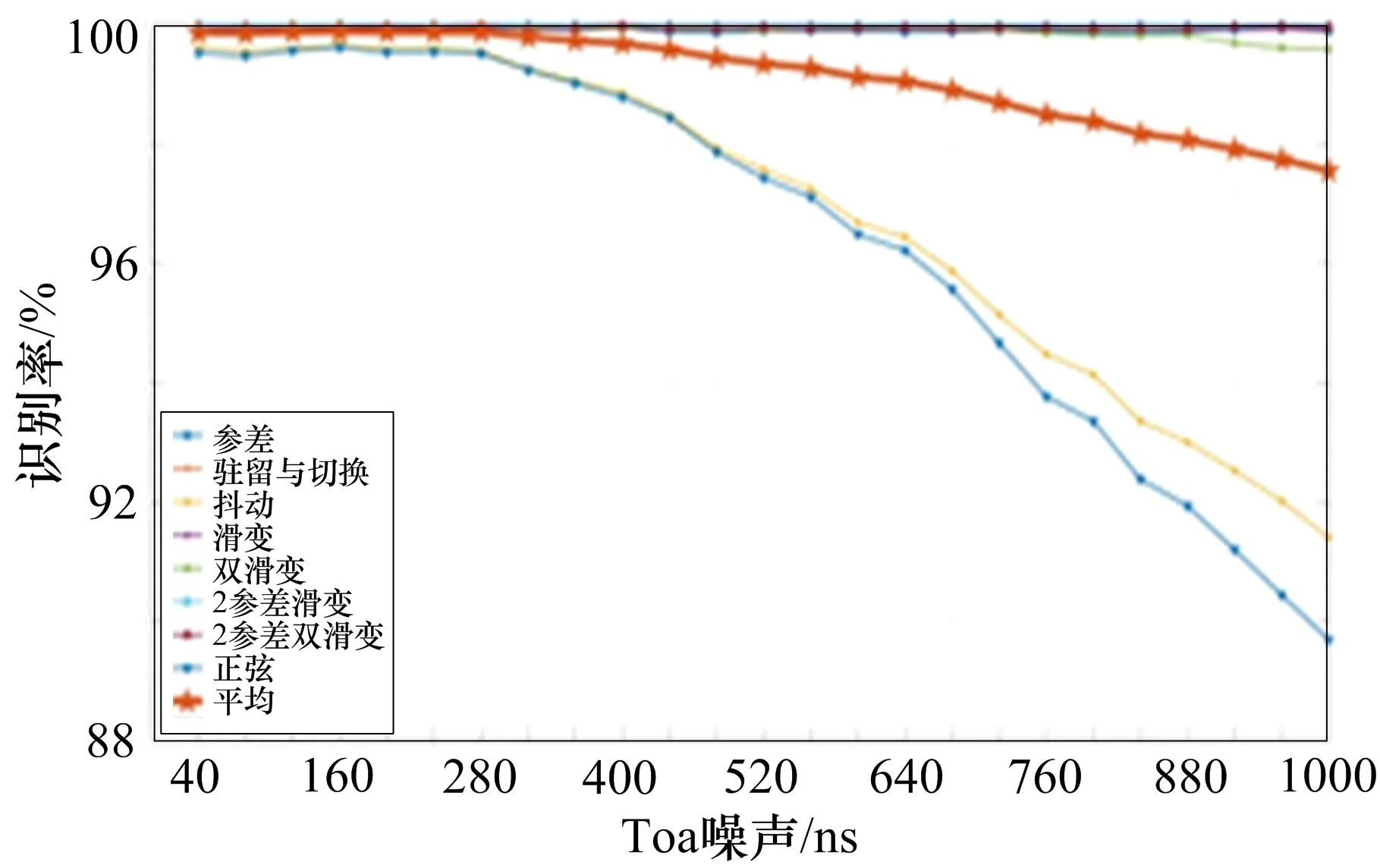
图6 测量噪声环境下PRI调制模式识别率

由实验结果可知，随着测量噪声增大，模型的识别率逐渐下降，但下降速度明显小于上2个实验。测量噪声从40 ns增加到1000 ns，模型的平均识别率始终保持在97%以上。当测量噪声不低于480 ns时，各种调制模式的正确识别率不低于97%。在测量噪声大于480 ns时，泛化能力不足。总体而言，模型在测量噪声影响下有着较好的识别能力。

3.4 小样本序列实验

上述实验中测试数据的每个样本都是由长度为128的PRI序列组成。为了验证不同长度的PRI序列对识别性能的影响，分别构造PRI序列长度为16～216的测试数据，使用模型分别对测试数据进行识别，识别结果如图7所示。

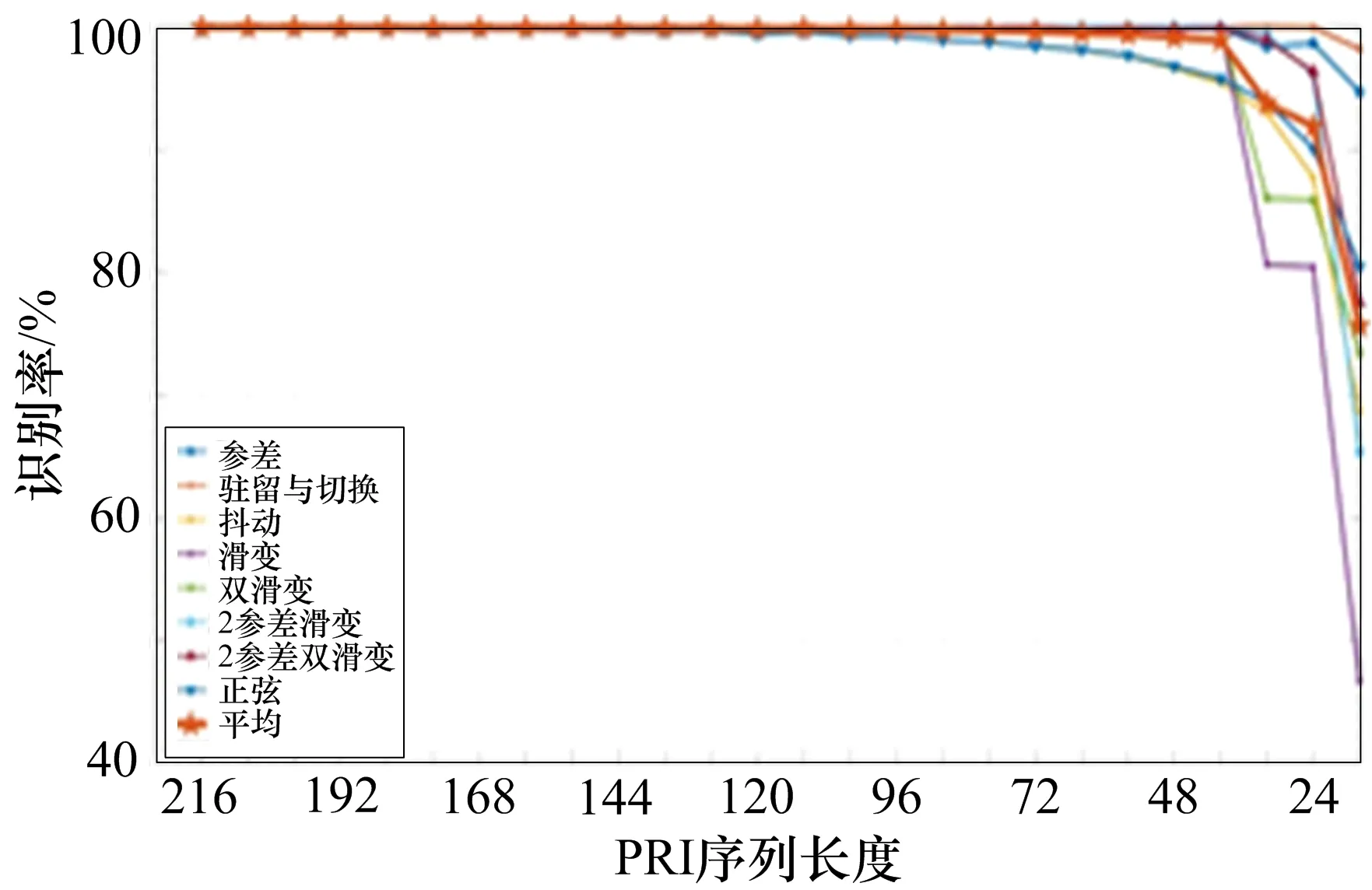
图7 短脉冲环境下PRI调制模式识别率

由图7可知，PRI序列长度不小于40时，模型的平均识别率在97%以上。当PRI序列长度小于40时，模型的识别率开始明显下降，尤其是2参差双滑变和双滑变调制模式。当PRI序列长度只有16时，平均识别率也接近80%。总体而言，本模型对于小样本序列有着较好的识别能力。

4 结束语

本文采用的深度卷积神经网络模型可以有效地对PRI调制模式进行识别，特别是当数据的PRI数量较小时模型仍有较好的识别性能，同时该方法抗测量噪声性能较好，对一定丢失和干扰环境下的测试数据识别能力出色。但与此同时，从模型对高丢失率和高干扰率数据的识别性能较差可以看出，当训练数据涵盖范围与测试数据差异较大时，模型的泛化能力不足。这也说明在实际使用中，训练数据要尽可能包含各种复杂电磁环境下的数据才能对实际采集信号有较好的识别性能。下一步的工作便是研究如何提高深度卷积神经网络在有限训练数据集上对测试数据的泛化能力以及实际工程应用上的实现。