“多元表征”导向深度学习
2019-12-11高红芝
高红芝

[摘 要]教师引导学生通过“多元表征”方式,探究发现小数点的位置移动引起小数大小变化的规律,并深刻理解这一规律,达到举一反三,灵活运用,进而实现深度学习。结合具体情境,探索出小数点的位置移动引起小数大小变化的规律,建立起小数点的位置移动与特殊的小数乘除法之间的联系,并能正确进行相关计算。笔者用多元表征,经历探索小数点移动引起小数大小变化规律的过程,发现并理解小数点移动引起小数大小变化的规律。在探索交流、归纳概括、合作互动等活动中,激发学生的学习兴趣,培养主动探索、合作交流的意识和能力。
[关键词] 多元表征; 移动; 规律
《小数点搬家》是北师大版四年级下册第三单元《小数乘法》中的第二课时,目的是通过“小数点的位置移动,引起小数大小变化的规律”的探索活动,鼓励学生借助以前学过的元角分之间的关系、数位顺序表、面积模型等多元表征方式,经历探索规律的过程,沟通新旧知识的联系,深刻理解小数点的位置移动引起小数大小变化的规律。
一、设疑激趣,引出课题
(一)谈话激趣
师:同学们,喜欢听故事吗?(喜欢)今天老师带来了一个故事,想不想知道?(想)请看大屏幕:课件出示主题情境图。
师:请仔细观察,看图编故事。谁来看图编一个故事?
生:森林里,蚂蚁老板开了一家快餐厅,开始价格是0.01元一份,客人很多,过了几天,老板发现客人是很多了,但生意却亏本,于是蚂蚁老板就把快餐涨价了,把价格提升到0.10元一份,客人就少了很多,但是生意却赚钱了,于是又过了几天,蚂蚁老板又把快餐涨价了,把价格提升到1.00元一份,就一个客人也没有,连小鸟都说太贵了!
师:你观察得真仔细,语言表达能力也很强,故事讲得很动听。
设计意图:让学生看图编故事,比老师直接讲故事,更能激发学生的兴趣,促使学生认真观察主题图,发现蚂蚁快餐厅客人变化的原因。
(二)引出课题
师:那蚂蚁快餐厅由顾客络绎不絕,到客人慢慢变少,再到最后一个客人也没有,是什么原因引起的呢?
生:是涨价了,价格越来越贵。
师:下面我们一起来观察这三个价格有什么不同。
板书: 0.01元 0.10元 1.00元
师:小数末尾的“0”也可以省略,大小不变。
生回答:价格越来越高,1的位置变了,小数点的位置变了。
师:今天我们就一起来研究“小数点搬家”中的学问。小数点搬家,也就是小数点移动。
设计意图:教师之前把小数末尾的0去掉,是为了不让这些0干扰到学生的观察。最后,让学生观察这三个数有什么不同,目的在于让学生多角度发现这三个数的不同点,从而导入课题,也为后面利用多元表征小数的大小关系做好铺垫。
二、探究新知,发现规律
(一)探究小数点向右移动引起小数大小变化的规律
1.动态演示小数点移动过程
师:现在老师请一名同学上台,让小数点动起来,看看这三个数是怎么转换的。其他同学认真观察,并用手势表示小数点的移动过程。
想一想:小数点是向哪边移动的?分别移动了几位?
生上台演示,其他学生用手势模拟小数点移动过程。
结合台上学生的回答,教师补充板书:
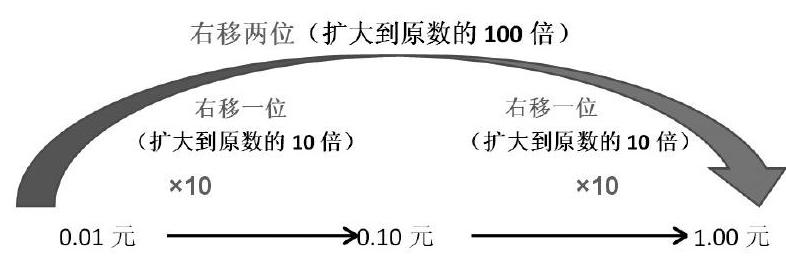
右移两位
[右移一位] [右移一位]
0.01元 0.10元 1.00元
生质疑:你是怎么判断小数点向右移动一位、两位的……
生:小数点向右边跨过一个数,就是小数点向右移动一位,小数点向右边跨过两个数,就是小数点向右移动两位。
师强调:小数点向右边跳过一个数,就是小数点向右移动一位,小数点向右边跳过两个数,就是小数点向右移动两位。
设计意图:让学生利用数字卡片和小圆片动态演示小数点向右移动的过程,旨在让学生通过实际操作,让小数点由静到动,形象直观,使学生掌握怎样向右移动小数点,学生的质疑,更好地突破了如何判断小数点移动的位数这一难点。
2.探究小数点向右移动引起小数大小变化的规律
师:小数点向右移动,小数的大小发生了什么变化?请用画图或算式的方法进行说明,并把你的发现写出来,然后在小组内交流你的方法。
学生活动:(1)学生尝试完成探究学习单(一);(2)小组交流;(3)汇报展示。
生1:方法一,元、角、分的关系:
0.01→0.10,小数点向右移动一位,1分变成1角,而1角是1分的10倍,所以0.10就扩大到原数的10倍。
0.10→1.00,小数点向右移动一位,1角变成1元,而1元是1角的10 倍,所以1.00就扩大到原数的10倍。
0.01→1.00,小数点向右移动两位,1分变成1元,而1元是1分的100倍,所以1.00就扩大到原数的100倍。
发现:小数点向右移动一位,得到的数是原数的10倍;小数点向右移动两位,得到的数是原数来的100倍。
生2:方法二,数位顺序表的方法;
[十位 个位 小数点 十分位 百分位 0 . 0 1 0 . 1 0 1 . 0 0 ]
0.01→0.10,小数点向右移动一位,原来百分位上的1现在到十分位上,相邻两个计数单位之间的进率是10,所以0.10就扩大到原数的10倍。
0.10→1.00,小数点向右移动一位,原来十分位上的1现在到个位上,所以1.00就扩大到原来的10倍。
0.01→1.00,小数点向右移动两位,原来百分位上的1现在到个位上,所以1.00就扩大到原来的100倍。
发现:小数点向右移动一位,得到的数是原数的10倍;小数点向右移动两位,得到的数是原数来的100倍。
生3:方法三、直观图形
0.01→0.10,小数点向右移动一位,10个0.01是0.10,所以0.10就扩大到原来的10倍。
0.10→1.00,小数点向右移动一位,10个0.10是1.00,所以1.00就扩大到原来的10倍。
0.01→1.00,小数点向右移动两位,100个0.01是1.00,所以1.00就扩大到原来的100倍。
发现:小数点向右移动一位,得到的数是原数的10倍;小数点向右移动两位,得到的数是原数来的100倍。
师:刚才同学们用了多种方法证明了小数点向右移动,小数大小的变化规律。我们一起来回顾刚才探索的方法,师生小结(补充板书)
右移两位(扩大到原数的100倍)
设计意图:通过多元表征,让学生经历探索小数点向右移动引起小数大小的变化规律的过程,沟通对已学知识的联系,积累数学活动经验,使学生不但掌握规律,更从多角度理解这一规律的算理。
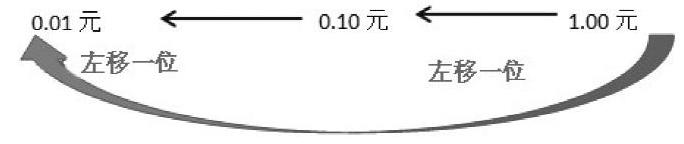
(二)探究小数点向左移动引起小数大小变化的规律
1.动态演示小数点向左移动过程
师:同学们的学习干劲真大,可蚂蚁老板急得团团转,这一个客人也没有,怎么办呀,同学们能帮帮它吗?(生:能)
生1:把價格降低
生2:把小数点向左移动
师:刚才同学们说得很好,把1.00元的小数点向左移动,把价格降低。也就是把0.01元 0.10元 1.00元从右往左观察。
师:这三个数小数点怎么向左移动转换呢?
一生上台演示,其他学生用手势模拟小数点移动过程。
思考:小数点分别向左移动了几位?你是怎么判断移动的位数的?
根据生回答师随机板书:
师强调:小数点向左边跳过一个数,就是小数点向左移动一位,小数点向左边跳过两个数,就是小数点向左移动两位。
设计意图:通过直观操作及手势模拟,让学生更容易掌握如何把小数点向左移动,及判断移动的位数。
2.探究小数点向左移动引起小数大小变化的规律
师:那小数点向左移动,小数的大小变化又有什么规律呢?
生汇报:可以用刚才探索小数点右移引起小数大小变化规律的方法。如:我刚才用的是元角分的转化方法,(生把探究学习单(一)上自己选择的方法拿上来投影)只是现在要倒过来看,就是从右往左观察。可以发现:小数点向左移动一位,得到的数就缩小到原数的10倍,小数点向左移动两位就可以缩小到原数的100倍。
师:倍一般用在扩大上,缩小到原数的10倍,我们讲缩小到原数的[110],那缩小到原数的100倍,就是缩小到原数的( )。生齐说:([1100])
师:刚才这个同学说得很好,那除了元角分转化的方法,我们也可以借助数位顺序表的方法和直观图的方法。
如:我们来看直观图的方法。(课件演示直观图的方法)
0.1是1的( ),0.01是1是( )。
指名学生回答,然后师生小结规律:
小数点向左移动一位,这个数就缩小到原数的[110];小数点向左移动两位,这个数就缩小到原数的[1100]。
设计意图:让学生迁移上一环节的探索方法,把结论过程化,旨在让学生掌握并理解小数点向左移动引起小数大小变化的规律。
(三)验证小数点移动引起小数大小变化的规律
师:刚才我们只是通过一组数据,就得出小数点左移和右移的规律,你们觉得行吗?为什么?
生1:不行,因为小数有很多,一个太少了。
生2:我也觉得不行,因为也许这组数就是一个特例,我们要举一些普通的小数,来验证一下看是不是也存在这种规律。
师:同学们说得真好,要使这个规律具有科学性和普遍性,我们要举大量的例子来验证。下面请同学们每人再举一个例子来证明。
学生活动:举例验证。
(1)学生独立完成探究学习单(二);(2)同桌交流;(3)汇报展示。
生1:我举的例子是,0.723 7.23 72.3
先看把小数点右移,从左往右看,我是用数位顺序表的方法来说明的:0.723的小数点向右移一位,变成7.23,小数点又向右移一位,变成72.3,第一个数的7在十分位上,第二个数的7向前挪了一位,现在个位上,第三个数的7向前挪了两位,在十位上,因为相邻的计数单位之间的进率是10,所以我证明小数点右移,数的大小变化规律符合刚才探索出来的规律。再从右往左看,就是小数点向左移动,同样从数位的变化可以看出小数点左移,数的大小变化规律符合刚才探索出来的规律。
师:同学们听了,觉得有问题想问吗?
生质疑:你只说了7这个数字的数位变化,就能证明整个数的大小变化吗?
生1忙补充:2和3这两个数字的数位也同样发生了相应的变化,所以说是符合刚才我们探究出来的小数点移动引起小数大小变化的规律。
师补充:刚才这个学生质疑得很好,只有当这个数中每个数位上的数都扩大到原数的10倍、100倍……我们才能说这个数扩大到原数的10倍、100倍……
当这个数中的每个数位上的数都缩小到原数的[110]、[1100]……,我们才能说这个数缩小到原数的[110]、[1100]……
生2、生3……
师生小结:通过举例子验证得出:
小数点向右移动一位,得到的数是原数的10倍;小数点向右移动两位,得到的数是原数来的100倍;小数点向右移动三位,得到的数是原数的1000倍……
小数点向左移动一位,得到的数就缩小到原数的[110];小数点向左移动两位,得到的数就缩小到原数的[1100];小数点向左移动三位,得到的数就缩小到原数的[11000]……
师:为什么规律后面打省略号呢?(生:说不完)你能接下去说一个吗?(能)
生:小数点向右移动四位,得到的数是原数的10000倍;小数点向左移动四位,这个数就缩小到原数的[110000]。
师:两位同学分别举出了个例子来验证(课件出示)。
设计意图:向学生渗透科学研究的意识,把规律的研究从特殊推广到一般,学生在验证与交流的过程中,进一步加深对规律的理解与认识。
三、动手实践,运用规律
(一)游戏活动
同桌两人合作:一人任意写一个数和指令,另一人按照指令操作,写出结果,然后两人任务轮换。
小数点向( 右 )移动(一)位
例如:小数(1.23)(12.3)
師:在同样的时间,比比看哪两人合作的成果又对又多。
1.学生活动; 2.成果展示
a.展示正例(略);
小数点向( 右 )移动( 三 )位
b.展示错例:小数( 2.5 )( 250)
小数点向( 左 )移动( 三 )位
小数(0.42) → (0.0042)
师逐一展示这两个错例,引导学生分析错误的原因。
师强调:小数点不管是左移还是右移,数位不够时要用0补足。
设计意图:同桌游戏,既培养了学生的合作意识,又让学生在游戏中巩固和应用所学的知识,寓教于乐;同时又对易错例进行分析,突破了小数点在移动过程中位数不够时要补0这一难点。
(二)提高练习
[5.18]
小数点先向左移动三位,再向右移动两位,得到的数是原数的( )。
设计意图:此题是一道较综合的题型,旨在培养学生思维的变通能力,除了会用两次分步操作完成外,还掌握用一次操作完成的简便方法,让学生理解这种简便方法的思维过程,培养学生的思维能力。
(三)拓展练习
考考你:把一个数先扩大到它的10倍,再缩小到它的[1100],最后再扩大到它的1000倍,得到的数是5.04,原来的数是多少?
设计意图:此题是一道逆向思维的题,旨在打破学生的思维定式,使学生掌握倒推方法,灵活解决问题,从而培养学生思维的灵活性。
“多元表征”导向深度学习。笔者以三个核心问题展开教学,考虑到四年级的学生正处于由具体形象思维到抽象逻辑思维发展的关键时期,所以鼓励学生尝试用元角分的关系、借助数位顺序表和面积模型等直观多元表征方式,来探索小数点的位置移动引起小数大小变化的规律,目的是让学生经历规律的探索过程,沟通新旧知识的联系,发现规律。在学生展示汇报多元表征方法的过程中,通过思考与交流,质疑与碰撞的深度对话,达到深刻理解规律的目的。让学生经历三个核心问题探索的全过程,既渗透科学研究的意识,把规律的研究从特殊推广到一般,又在探索与验证的过程中,通过多元表征方式,沟通新旧知识的联系,使知识条理化、系统化,进而逐步加深对规律的理解与认识,实现真正意义上的深度学习。
责任编辑 吴晶晶
