十字轴式万向联轴器运动学再研究
2019-12-11徐永帅王佳伟徐慧茹
徐永帅,陈 纯,房 舟,王佳伟,徐慧茹
(陕西理工大学 机械工程学院, 陕西 汉中 723000)
十字轴式万向联轴器可用来连接两相交轴,作为机械传动中的重要部件,自问世以来受到广大专家、学者的青睐。由于具有结构简单、使用寿命长、传动效率高、维护方便等优点,在汽车等行业得到广泛应用[1-4]。十字轴式万向联轴器在连接两相交轴时,由于两轴间存在夹角,会使得输出轴的转动存在速度波动,传递运动与动力不平稳。因此许多专家、学者先后对其运动特性做了分析,如范景峰等[5]对单十字轴利用平面法线的运动轨迹对联轴器的运动规律做了研究;陈科等[6]利用空间几何投影的方法建立了双联虎克万向节的运动过程,分析了联轴器传动比及转角差的影响因素;王学锋等[7]利用数值方法对三叉滑移型联轴器机构在单径向轴承和调心轴承安装时进行了理论分析,得到其为一种准等角速万向联轴器的结论;常德功等[8]利用空间机构坐标变换方法对三叉杆滑块式万向联轴器做了运动分析;李宁等[9]定量分析了相位角对传动比的影响,得出传动轴相位角与传动面夹角相等且方向相反时对传动比影响最小。同时也有其他专家、学者对不同的万向联轴器做了大量的研究[10-14]。
为了了解十字轴式万向联轴器在不同轴间夹角下输入、输出轴间的运动关系,本文拟通过建立联轴器的空间模型,运用向量法对其进行研究。最后运用ADAMS仿真,并进行数值分析,验证所建立的模型及分析结果的正确性。
1 运动学建模
十字轴式万向联轴器如图1所示,输入轴与输出轴通过十字轴连接,在联轴器上建立坐标系,输出轴的轴线与Y轴重合,十字轴的水平轴线与X轴重合,根据右手定则确定Z轴,输入轴轴线与Y轴正向的夹角定义为β(即输入、输出轴间的夹角为β)。
根据所建立的十字轴式万向联轴器的三维模型,将三维摸型转换为空间几何模型,如图2所示。△ABC和△EFG分别表示十字轴式万向联轴器的输出轴和输入轴的平衡位置,其中OA和OG分别表示输出、输入轴的轴线,OG与Y轴正向夹角为β。当输入轴(△EFG)绕着其轴线OG以角速度ω1旋转α1角度时,相应的输出轴(△ABC)会绕着其轴线OA以角速度ω2旋转α2角度,此时输出、输入轴分别到达新的位置(△A′B′C′、△E′F′G′)。

图1 十字轴式万向联轴器模型 图2 联轴器空间几何模型
从十字轴式万向联轴器的三维模型中可知十字轴的水平轴和竖直轴相互垂直,即BC⊥EF,亦即OB⊥OF,同理可知在新的位置同样有OB′⊥OF′。
由于直线OG与Y轴正向夹角为β,故直线EF与Z轴的夹角也为β,当输入、输出轴分别绕着其轴线OG、OA分别以角速度ω1、ω2旋转α1、α2角度时,假设OB=OF=R,则在新的位置(△E′F′G′、△A′B′C′)易得点B′的坐标为(Rcosα2,0,Rsinα2),故OB′={Rcosα2,0,Rsinα2}。
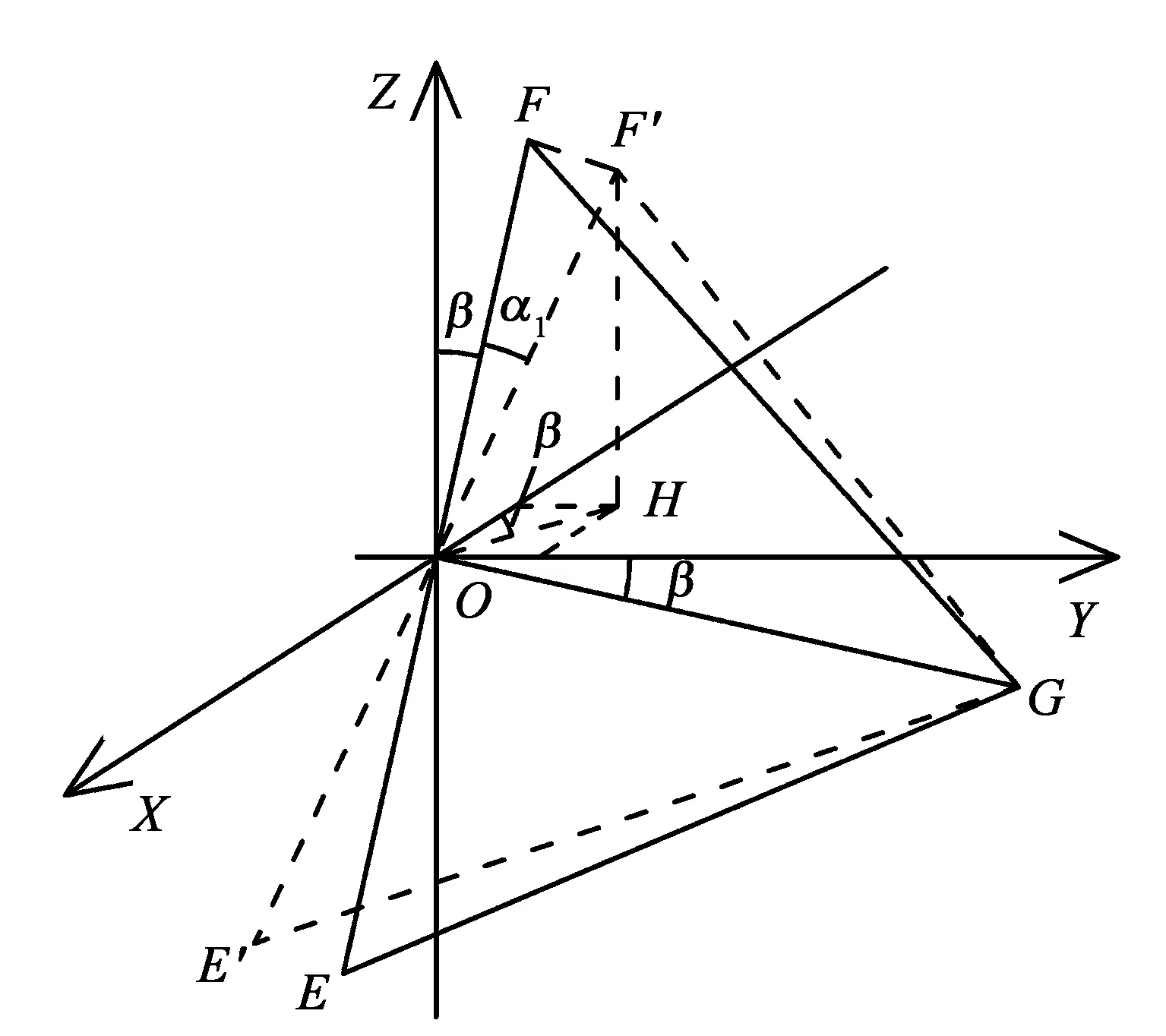
图3 输入轴空间模型


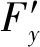
则F′的坐标为(-Rcosβsinα1cosβ,Rcosβsinα1sinβ,Rcosβcosα1),故
OF′={-Rcosβsinα1cosβ,Rcosβsinα1sinβ,Rcosβcosα1}。
又由OB′⊥OF′,即
OB′·OF′=0,
(1)
{Rcosα2,0,Rsinα2}·{-Rcosβsinα1cosβ,Rcosβsinα1sinβ,Rcosβcosα1}=0,
(2)
整理式(2)可得:
(3)
整理式(3)得:
α2=arctan(cosβtanα1),
(4)
式(4)即为十字轴式万向联轴器的位置方程;
将式(4)对时间求导得联轴器的速度方程:
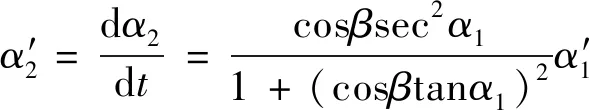
(5)
将式(4)对时间求二阶导数得联轴器的加速度方程:

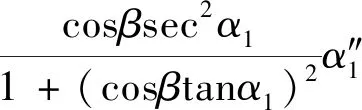
(6)

2 运动学仿真
为了验证所建立的十字轴式万向联轴器运动学模型的正确性,利用ADAMS仿真软件对联轴器进行运动学仿真分析。
分析可知联轴器前半个周期的运动与后半个周期完全相同,故这里只做其前半个周期的仿真分析。给输入轴输入ω1=10 (°)/s(t∈[0,18 s])的转动速度,分别对输入、输出轴轴间夹角β=0°、25°、45°时进行仿真分析(β=0°时的输出轴转动状态可代表不同β值下输入轴的转动状态),仿真结果如图4—图6所示。

图4 转动角度曲线 图5 转动速度曲线
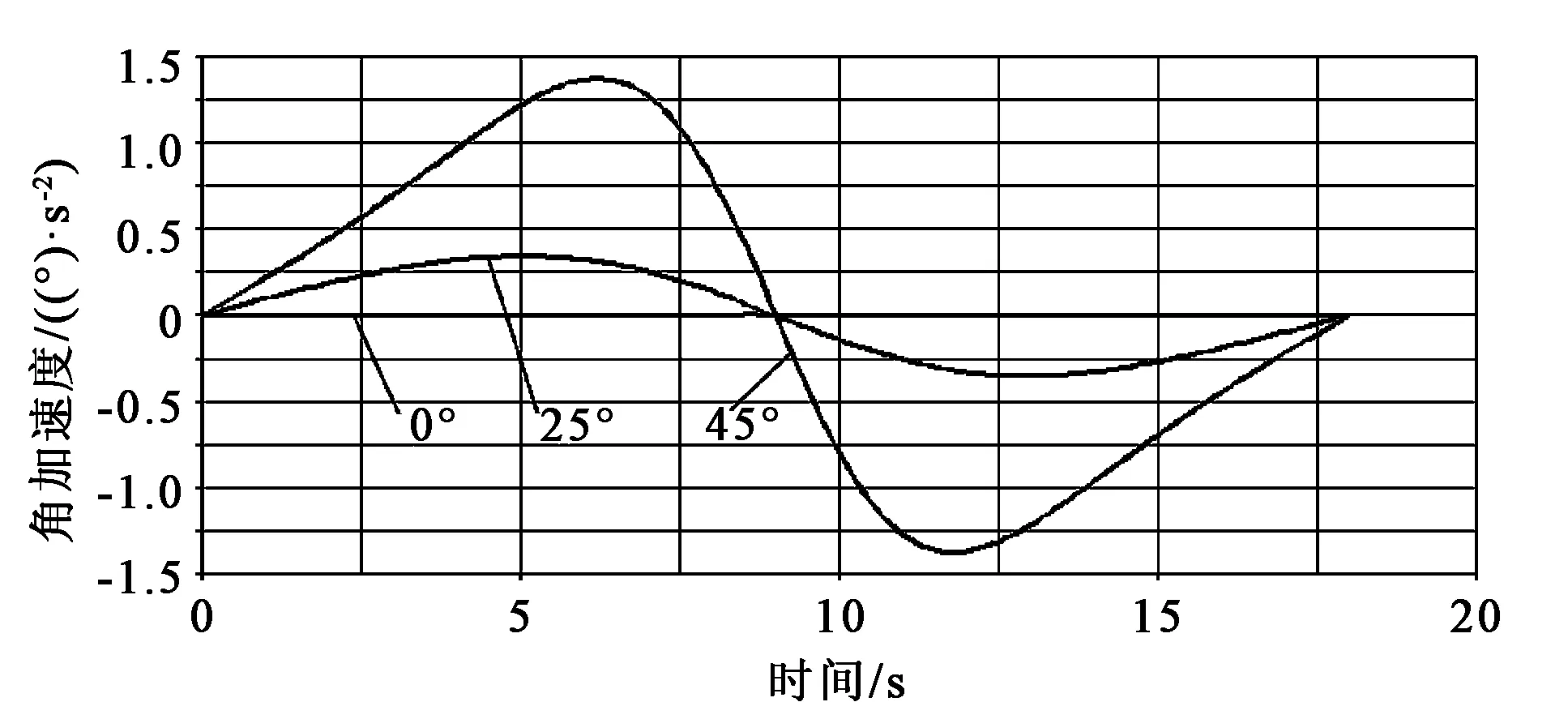
图6 转动加速度曲线
分析图4可知,给输入轴输入ω1=10 (°)/s的转动速度,当输入、输出轴轴间夹角β=0°时,输入、输出轴的转角是相同的(均为一条倾斜的直线),转角差为0,当β=25°时输出轴转角曲线与输入轴产生偏差,当β=45°时输出轴转角曲线与输入轴有明显偏差。在β=25°、45°时,输出轴转角曲线前9 s处于β=0°曲线(输入轴转角曲线)的下方,后9 s处于上方,且随着输入、输出轴轴间夹角β的增大,输出轴转角曲线偏离β=0°曲线的程度也在增大。在t=9、18 s时(90°、180°)三条曲线重合。
分析图5可知,输入、输出轴夹角β=0°时其转速完全相等(均为10 (°)/s),β≠0°时输出轴的转速随着夹角β的增大偏离输入轴的程度越大,且转速均在前9 s逐渐增大,后9 s逐渐减小,并关于t=9 s处对称。β=25°时,在t∈[0,4.6 s]与[13.4 s,18 s]上输出轴转速小于输入轴,在[4.6 s,13.4 s]上大于输入轴转速;β=45°时,在t∈[0,5 s]与[13 s,18 s]上输出轴转速小于输入轴,在[5 s,13 s]上大于输入轴转速。t=9 s时速度达到最大,t=0、18 s时速度最小且相等,β=25°时速度最大为11.033 8(°)/s,最小为9.065 1(°)/s,β=45°时速度最大为14.143 8(°)/s,最小为7.035 7(°)/s。
分析图5亦可知,β≠0°时输出轴在前9 s加速大于零,后9 s加速度小于零,在9 s时加速度等于零,速度达到最大,且加速度曲线关于t=9 s处成中心对称,这与速度曲线图像分析结果是一致的。β=0°时输出轴加速度恒为0。β=25°时,在t=5 s处加速度达到最大为0.347 2(°)/s2,在t=13 s处加速度最小为-0.347 2(°)/s2;β=45°时,在t=6.2 s处加速度达到最大为1.374 0(°)/s2,在t=11.8 s处加速度最小为-1.374 0(°)/s2。
为了验证所建立的运动学模型的正确性,分别取t=3、6、9、12、15 s时不同β值下的理论计算值与仿真值进行比较,结果如表1所示。

表1 不同β值下的理论计算值与仿真值
分析表1中的数据可知,在β=25°时,理论计算值与仿真值的角度最大偏差为0.001°,速度最大偏差为0.000 4 (°)/s,加速度最大偏差为0.000 2(°)/s2;β=45°时,理论计算值与仿真值的角度最大偏差为0.003 6°,速度最大偏差为0.000 5 (°)/s,加速度最大偏差为0.000 2(°)/s2,偏差均很小。输出轴转速关于t=9 s(90°)成对称关系,加速度关于t=9 s(90°)成中心对称关系。随着β的增加,各数据偏离t=9 s时数据的程度也越大,这与仿真曲线的分析结果一致,再次证明了运动学模型的正确性。
3 结 论
根据所建立的十字轴式万向联轴器的运动学方程以及对该联轴器的运动学仿真分析,可得出以下结论:
(1)十字轴式万向联轴器的一个完整的运动周期内包含着两个运动状态完全相同的半周期;
(2)在其半个周期内,输出轴的角速度关于其转角90°处成轴对称关系,角加速度成中心对称关系;
(3)随着输入、输出轴间夹角β的增大,输出轴运动状态曲线偏离输入轴的程度越大,但在输入轴运动状态曲线的两侧周期性的波动。
