引入序列信息的残基相互作用网络比对算法∗

陶斯涵 , 丁彦蕊,2

1(江苏省媒体设计与软件技术重点实验室(江南大学),江苏 无锡 214122)

2(工业生物技术教育部重点实验室(江南大学),江苏 无锡 214122)

生物网络,例如蛋白质-蛋白质相互作用网络、代谢网络、残基相互作用网络、基因表达网络等[1],已经成为大数据时代生命科学相关研究的重要数据资源.这使得生物网络比对在近年来成为研究代谢、结构、功能和进化的有效的方法.通过生物网络比对的方法可以发现两个或两个以上相互作用网络在拓扑和功能上的相似区域,用于研究生物分子的结构和功能,分析生物的进化和演变.

通常,功能相似的蛋白质分子具有相似的空间结构,而结构上局部的差异可能会导致其性质的不同,如蛋白质的热稳定性、亲水性、疏水性、耐酸性、耐碱性等[2].残基相互作用网络对于从系统角度研究蛋白质空间结构和蛋白质性质、功能的关系有着至关重要的作用.而残基相互作用网络比对,对于研究蛋白质的分子基础和空间结构非常重要,是探究蛋白质空间结构与蛋白质性质、功能异同关系的有效方法.

目前,绝大多数的网络比对方法是针对蛋白质-蛋白质相互作用网络(简称PPI 网络)提出的.PPI 网络比对可以分为全局网络比对和局部网络比对.局部网络比对旨在找到小的、高度保守的子网络,而不考虑比较网络的整体相似性[1],例如PathBLAST[3]、MaWISH[4]和AlignMCL[5]等.PathBLAST 是最早的局部网络比对算法.它通过蛋白质-蛋白质相互作用网络中保守路径和比对蛋白质之间同源性的概率来搜索高分比对.MaWISH 模拟生物的复制和删除,并利用网络的加权边找到最大权重诱导子图.AlignMCL 将单个比对图中的许多蛋白质相互作用网络合并,并在随后将其挖掘用于识别不同物种中的保守子网.全局网络比对旨在最大化网络之间的整体匹配.它产生一对一的节点映射,较小网络中的每个节点都被映射到较大网络中的一个唯一的节点[1],例如IsoRank[6]、GRAAL[7]、MI-GRAAL[8]、HubAlign[9]、MAGNA[10]和ModuleAlign[11]等.IsoRank 是第一种全局网络比对算法,将PPI 网络中蛋白质的易匹配序列和邻域拓扑结构比作特征值问题,并求得网络的最佳匹配.GRAAL 基于所有邻居节点的拓扑相似性,利用贪心算法找到最优比对.MI-GRAAL 整合了网络节点之间的任何数量和类型的相似性标准,并决定了相似性标准间的权重,利用最大权重双边图找出最优比对.HubAlign 使用启发式算法,从网络拓扑信息的方面对蛋白质的拓扑结构和功能的重要性进行评估,并优先比对拓扑结构重要性高的蛋白质.MAGNA 是一种基于PPI 网络拓扑信息的全局网络比对算法.它利用遗传算法框架,将两个“父代”比对通过交叉函数“交叉”产生优秀的“子代”比对,保留并进入下一代,直到达到停止条件,输出最优的比对.ModuleAlign 利用局部信息来定义模块的同源性分数,基于参与相同模块的功能相关蛋白质的分层聚类,并采用迭代方案找到两个网络之间的比对.目前,蛋白质-蛋白质相互作用网络比对主要应用于功能预测和系统发生分析等相关研究.

众所周知,影响蛋白质相似性的因素是多方面的,其中最主要的是蛋白质序列的相似性和空间结构的相似性.蛋白质序列相似的分子往往具有相似的结构或相似的功能.但序列相似的分子在高级结构和功能上并不具有必然的相似性[12].因此,将蛋白质的三维结构编码为残基相互作用网络,对网络进行比对,是从系统角度分析蛋白质功能与结构及序列的关系的主要途径.

然而,目前一般采用PPI 网络比对算法对残基相互作用网络进行比对,还没有针对残基相互作用网络的比对算法,这就忽视了氨基酸残基本身的信息.因此,在对上述PPI 网络比对的各种算法分析的基础上,本文基于MAGNA 网络比对方法,将蛋白质的序列信息即残基匹配度引入到优化函数中,提出了针对残基相互作用网络比对的SI-MAGNA 算法.同时,与其他现有的基于网络拓扑信息的经典比对方法(GRAAL[7]、MI-GRAAL[8]、MAGNA[10]、CytoGEDEVO[13])相比较,边正确性表明,SI-MAGNA 算法在残基相互作用网络比对方面优于其他的方法.最后,对不同耐热性的同源蛋白质的残基相互作用网络使用SI-MAGNA 方法进行网络比对和分析,探索蛋白质结构对其热稳定性的影响.

本文第1 节对SI-MAGNA 方法的算法框架和原理进行总结.第2 节构建一系列蛋白质的残基相互作用网络对,并使用SI-MAGNA 算法进行比对.其中,第2.1 节中总结拓扑信息-序列信息权重α对比对结果的影响程度,并与MAGNA 方法进行比较;第2.2 节中使用SI-MAGNA 方法与其他现有的基于网络拓扑信息的经典比对方法(GRAAL[7]、MI-GRAAL[8]、CytoGEDEVO[13])相比较,以验证SI-MAGNA 方法的优越性;第2.3 节中介绍SI-MAGNA 方法的应用.第3 节总结全文.

1 原理与方法

1.1 残基相互作用网络的构建

构成蛋白质序列的基本单位是氨基酸残基,简称残基.将残基相互作用网络定义为一个无加权图,节点表示残基,边表示不同残基间的相互作用.为了判定相互作用的存在性,将残基的Cα的坐标作为残基的位置,计算不同残基间的距离,当残基间的距离小于6.5Å 时,认为相互作用存在[14-16].假定两个残基相互作用网络分别为G1=(V1,E1)和G2=(V2,E2),V1和V2表示节点的集合,E1和E2表示边的集合.令m=|V1|,n=|V2|,|V1|≤|V2|.残基相互作用网络G1到G2的比对定义为f:v1→v2.节点集V1中每一个节点到V2中的节点都存在一对一的映射.

1.2 SI-MAGNA方法思想

MAGNA 方法是一种基于PPI 网络的两两全局比对算法.它只利用网络的拓扑信息产生比对.它基于遗传算法框架,使用交叉函数使两个“父代”比对产生一个优秀的“子代”比对,并迭代计算直到达到停止条件,获得比对结果[10].

1.2.1 交叉函数

交叉函数是MAGNA 方法的核心[10].它主要由以下3 个步骤组成(如图1 所示).交叉函数通过节点标号对应节点标号的形式来表示任何比对f(即一个对应的排列σ).建立图Γn,它具有节点集Sn和边集En,其中,Sn为所有排列σ的集合,当且仅当排列σ和τ邻接时,En表示排列σ和τ之间的边的集合.排列σ和τ交叉(表示为σ⊗τ)表示图Γn中从σ到τ最短路径的近中点.因此,将两排列交叉产生的子比对定义为两个父比对之间的“中间”比对,子比对预计将继承其每个父比对的大约1/2.SI-MAGNA 算法采用相同的交叉函数.

Fig.1 Main operation of the cross function图1 交叉函数的主要操作

1.2.2 基于遗传算法的框架

遗传算法是一种启发式搜索算法.它借鉴生物界适者生存的进化规律.MAGNA 方法基于遗传算法,迭代搜索以获得最优的比对[10].SI-MAGNA 算法采用相同的搜索策略.

通过随机比对以获得给定规模p的初始种群P0,种群中的成员即比对.为了防止种群规模的无限增长,只有“适者”能够生存到下一代.对于每一代种群P,通过适应度函数F,将种群中的成员以其比对质量从高到低排序,设定精英率e,将种群中占比为e的“高质量”成员保留作为子代成员直接加入下一代种群中.

接下来,使用Roulette 选择算法选择种群P中的成员进行“交叉”产生新的子代,以补足下一代中剩余的部分,所选择成员的概率与成员的适应度成正比.种群中成员被选中的概率可表示为

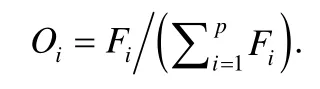
随着算法的进行,种群中成员的适应度(比对质量)逐渐增加,直到达到停止条件,输出最优比对.

1.3 适应度函数

适应度函数F作为网络比对的优化条件,在算法中起到至关重要的作用.考虑残基相互作用网络的特点,这里将适应度函数F定义为

其中,TopoScore(f)表示拓扑信息(详见第1.3.1 节),SeqScore(f)表示序列信息(详见第1.3.2 节),权重α用来调整拓扑信息和序列信息对比对的影响作用.拓扑信息-序列信息权重α的取值范围是[0,1],当α等于1 时,表示只引入拓扑信息,而不考虑序列信息;当α等于0 时,表示只引入序列信息,而不考虑拓扑信息.

1.3.1 拓扑信息TopoScore(f)

拓扑信息TopoScore(f)使用对称子结构得分(S3)[10].由网络G1(V1,E1)和G2(V2,E2)的比对f:v1→v2,设G2[Y]为点集为Y的G2的子网,f(V1)={f(v)∈V2:v∈V1},f(E1)={(f(u),f(v))∈E2:(u,v)∈E1}.并将保守边定义为由通过f比对的两个网络的两条边组成(如图2 所示),即当G1中的节点u,v通过f分别比对上G2中的节点u′,v′时,那么边(u,v)和边(u′,v′)构成一条保守边.对称子结构得分(S3)表示保守边的数量占网络G1和G2[f(V1)]叠加的复合图边的数量的比例,它既惩罚了比对从密集区域映射到稀疏区域,又惩罚了从稀疏区域映射到密集区域[10],表示为

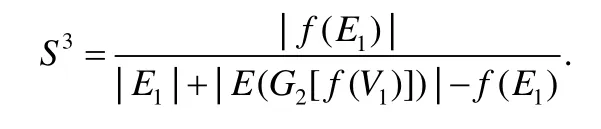
Fig.2 Illustration of conserved edges图2 保守边示意图

1.3.2 序列信息SeqScore(f)

序列信息SeqScore(f)使用基于BLOSUM 矩阵[12]的残基匹配度矩阵进行评价.本文基于BLOSUM 矩阵是因为该矩阵基于蛋白质进化的星状模型(即忽略物种近端和远端的关系)和区块中的保守位置与置换关系进行计分,这对于发现同源蛋白质中的保守区域有非常重要的作用.由于蛋白质的功能是由序列和特定的空间结构等因素共同决定,在残基相互作用网络比对中,只利用网络的拓扑信息无法获得在网络拓扑和一级结构方面更准确更合理的比对结果.因此,本文引入蛋白质的序列信息,并定义残基匹配度矩阵,加入到网络比对的适应度函数中.

残基匹配度矩阵是通过统计蛋白质序列的替换率而得到的氨基酸矩阵,由蛋白质序列块比对推导得出.其大致步骤如下.

首先,消除相似度小于指定阈值的序列,计算数据中每个氨基酸组合发生的可能性和该组合预期发生的可能性比率Log-odds,表示为

其中,P(O)表示观察的可能性,P(E)表示预期的可能性.

然后,基于此计算残基匹配度矩阵,表示为

其中,ij是氨基酸i与j在同源序列中相互替换的概率;qi和qj是氨基酸出现在任意蛋白质序列中的概率;λ是一个尺度参数,使每个得分更易取整.

使用残基匹配度矩阵作为序列信息计算网络G1中的任意节点vi与网络G2中任意节点vj相匹配时的替换率,并作为匹配度并用矩阵存储.同时,为了保证适应度函数的合理性,其数量级需要与拓扑信息一致.这里采用min-max 方法对残基匹配度矩阵进行标准化,具体表示为

其中,x表示某两个残基的匹配度,x*表示标准化后某两个残基的匹配度,max 为矩阵中的最大值,min 为矩阵中的最小值.此时,序列信息与拓扑信息处于同一数量级,适合进行综合比对评价.

综上所述,算法步骤如下,并可由算法流程图表示(如图3 所示).

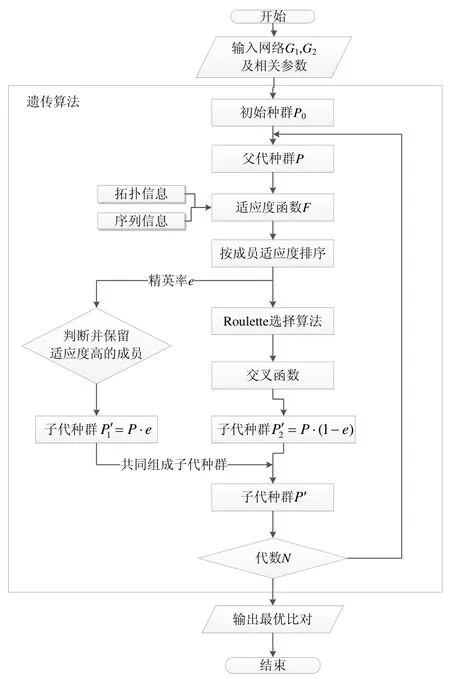
Fig.3 SI-MAGNA algorithmic framework图3 SI-MAGNA 算法流程图

(1)输入网络G1,G2及相关参数:代数N、精英率e、种群规模p.

(2)随机产生种群规模p的比对初始种群P0.

(3)以初始种群P0作为父代种群.

(4)设置代数计数器n=1.

(5)通过适应度函数F,计算父代种群P中成员的适应度,并进行排序.

(6)判断并保留适应度高的父代种群成员,保留比例为精英率e,即

(7)通过Roulette 选择算法和交叉函数产生适应度较高的比对成员,补足剩余的部分,即

(8)将步骤(5)和步骤(6)产生的比对成员组成子代成员P′.

(9)当n达到代数N时,终止循环.

(10)输出网络比对结果.

1.4 网络比对算法的性能评估

目前,边正确性(edge correctness,简称EC)广泛应用于网络比对算法的性能评估,通常通过计算EC 来评价网络比对结果的优劣[7,8,10,13].EC 表示比对中保守边的数量占网络G1边的数量的比例.当一个输入网络G1与另一网络G2是同构的时,它取得最高值100%.EC 可表示为

2 结果与讨论

在本文中,为了验证SIMAGNA 网络比对方法,从RCSB PDB 数据库(http://www.rcsb.org/pdb/home/home.do)下载了不同蛋白质的三维结构信息和序列信息,构建残基相互作用网络进行比对.在这里,主要对以下9 组网络对数据进行比对分析,见表1,其中,每组网络对的序列相似性由BLAST 序列比对算法(https://blast.cbi.nlm.nih.gov/Blast.cgi)两两比对得出.

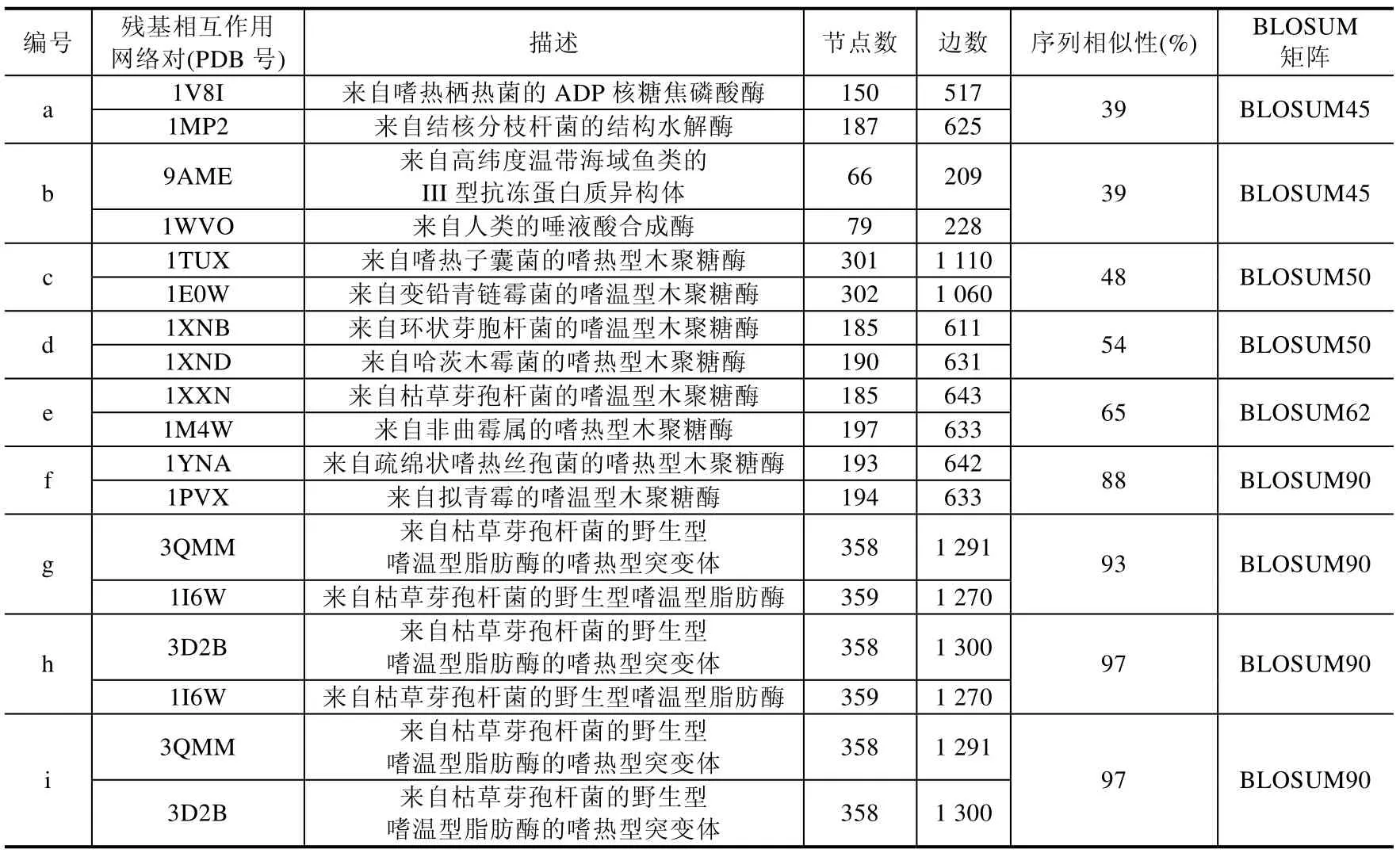
Table 1 Information of residue interaction network for different proteins表1 不同蛋白质的残基相互作用网络的基本信息

为了评估引入了蛋白质序列信息(残基匹配度)的SI-MAGNA 方法以及其他网络比对方法(GRAAL[7]、MI-GRAAL[8]、MAGNA[10]和CytoGEDEVO[13]),选择受到广泛认可的EC 作为评估网络比对质量的标准[7,8,10,13].

2.1 基于SI-MAGNA方法的残基相互作用网络比对

本文选择了来自不同物种的具有相似功能或结构的蛋白质进行残基相互作用网络的比对,以验证SIMAGNA 网络比对方法.实验设置初始种群P0为15 000,精英率e为0.5.

拓扑信息-序列信息权重α是影响比对结果的重要因子,它的取值范围是[0,1].在实验中,设定代数N为2000,α取值步长为0.1.上述9 组残基相互作用网络比对组实验结果如图4 所示,图中横轴为拓扑信息-序列信息权重α取值,纵轴为EC 值,每条折线分别表示各组比对.

Fig.4 Influence of TopoScore-SeqScore weight α on the SI-MAGNA alignment results图4 拓扑-序列信息权重α对SI-MAGNA 方法下比对结果的影响

从实验中发现,当α=0 时,表示只引入网络的序列信息到适应度函数中进行比对,其EC 接近0,表明网络比对效果非常差;同样地,当α=1 时,表示只引入网络的拓扑信息到适应度函数中进行比对,其边EC 也很低.这说明在残基相互作用网络的比对中,仅依靠网络的拓扑信息或序列信息均不能获得很好的比对结果.当α={0.1,0.2,…,0.9}时,表示分别以一定比例引入拓扑信息和序列信息到适应度函数中,发现比对结果的EC 有较大的提升;同时,比对得到的共同保守子图规模也更大.这说明尽管网络拓扑信息是网络比对优化的基础,但在残基相互作用网络比对中,仅用拓扑信息进行比对优化不够全面,序列信息对于残基相互作用网络而言也十分重要,将它引入比对优化的适应度函数中,能够明显地提升比对质量,获得更优的结果.

为了探究改进后的方法在残基相互作用网络比对方面的可靠性,在原方法探讨所得的基础上对代数N进行了进一步实验,同时以原方法作为参照.在实验中,拓扑信息-序列信息权重α取各组在N=2000 时产生最优比对时的值,代数N取值为2000、4000、6000、8000、10000、120000.上述9 组残基相互作用网络对比对实验结果如图5 所示,图中横轴为代数N,纵轴为EC,实线表示SI-MAGNA 算法,虚线表示MAGNA 算法,各组网络对分别为:(a)1V8I&1MP2;(b)9AME&1WVO;(c)1TUX&1E0W;(d)1XNB&1XND;(e)1XXN&1M4W;(f)1YNA&1PVX;(g)3QMM&1I6W;(h)3D2B&1I6W;(i)3QMM&3D2B.从实验中发现,对于改进后的方法SI-MAGNA,代数N的取值变化对于比对结果的影响很小,比对结果的EC 保持在较高范围内浮动.而对于MAGNA 方法,代数N的取值变化对于比对结果的影响较大,比对结果的EC 在大多数情况下是在逐渐增加后进入平稳,也会在很少情况下出现比对结果的EC 保持在相对高的范围内浮动.这说明在残基相互作用网络比对方面,MAGNA 方法在大多数情况下比SI-MAGNA 需要更多的代数才能得到较好的比对结果,且最终比对结果的EC 往往不如改进后的方法SI-MAGNA 高.此外,由于某些残基相互作用网络对的网络规模较小,会在较少情况下出现比对结果比较好(EC 值较高)且在小范围浮动的情况.图中结果说明,SI-MAGNA 方法表现更加稳定,在较少的代数N时,已经能够获得较好且相对稳定的比对结果.并且相对于原方法,改进后的SI-MAGNA 方法不但取得了更优的比对结果,而且因为更少的代数而提高了比对的效率.

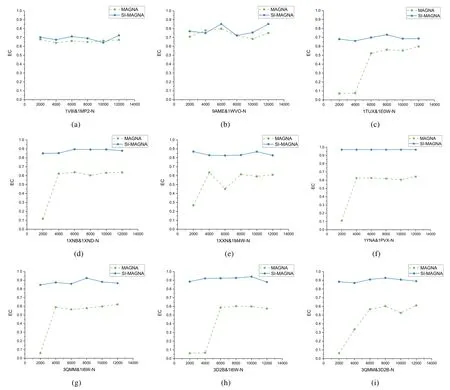
Fig.5 Influence of generation N on the SI-MAGNA alignment results图5 代数N 对SI-MAGNA 方法下比对结果的影响

2.2 与其他网络比对方法对比

为了验证引入蛋白质序列信息的SI-MAGNA 算法在残基相互作用网络比对方面的优越性,选择基于网络拓扑信息的其他网络比对方法与之比较.由于目前绝大多数的生物网络比对方法是针对蛋白质-蛋白质相互作用网络的,这些方法中的许多方法融入了蛋白质节点的生物信息(如BLAST-E 值、基因本体论正确性[17]等),因此,这类方法不适用于残基相互作用网络的比对.为了保证比对实验的合理性,目前一般采用仅基于网络拓扑信息的PPI 网络比对算法对残基相互作用网络进行比对,选择的方法是GRAAL、MI-GRAAL 和CytoGEDEVO方法.4 种比对方法的基本设置如下.

(1)SI-MAGNA 方法.在实验中,设置初始种群P0为15 000,精英率e为0.5,代数N为2 000,拓扑信息-序列信息权重α在[0,1]中取值,步长为0.1,并在结果中择优.

(2)GRAAL 方法.GRAAL 方法是基于graphlet 度特征相似性的网络比对算法.它基于邻居节点的拓扑相似性寻找最优比对,适用于任何网络的比对.为了保证算法比较的合理性,在实验中,节点-边权重α在[0,1]中取值,步长为0.1,其他使用默认设置,并选择最优比对结果.

(3)MI-GRAAL 方法.MI-GRAAL 方法整合了网络节点之间多种类型的相似性标准,并决定它们的权重,以此找到最优比对.为了保证算法比较的合理性,在实验中,剔除默认方法中基于蛋白质生物信息的相似性标准(BLAST-E 值),选择基于网络拓扑性的相似性标准的组合(graphlet 度特征、度、聚类系数、节点离心率和介数得分),使方法完全基于网络的拓扑相似性进行比对,并选择各相似性标准组合中的最优比对结果.

(4)CytoGEDEVO 方法.GEDEVO 方法[18]基于进化算法,使用图编辑距离作为优化模型来找到最佳比对.CytoGEDEVO 方法是基于GEDEVO 方法的CytoScape 软件上的扩展.为了保证算法比较的合理性,在实验中,设置迭代次数为2 000,其他使用默认设置.

上述9 组残基相互作用网络对比对实验结果如表2 和图6 所示(图6 中,横轴表示各组残基相互作用网络对,纵轴为EC,每组柱状图从左到右分别表示SI-MAGNA、GRAAL、MI-GRAAL、CytoGEDEVO 的比对结果的EC).从实验中发现,SI-MAGNA 方法在各组网络对中均获得更优的比对结果,具有更高的EC.这证实了SI-MAGNA 方法在残基相互作用网络比对方面的表现更为出色,优于另外3 种拓扑网络比对方法.

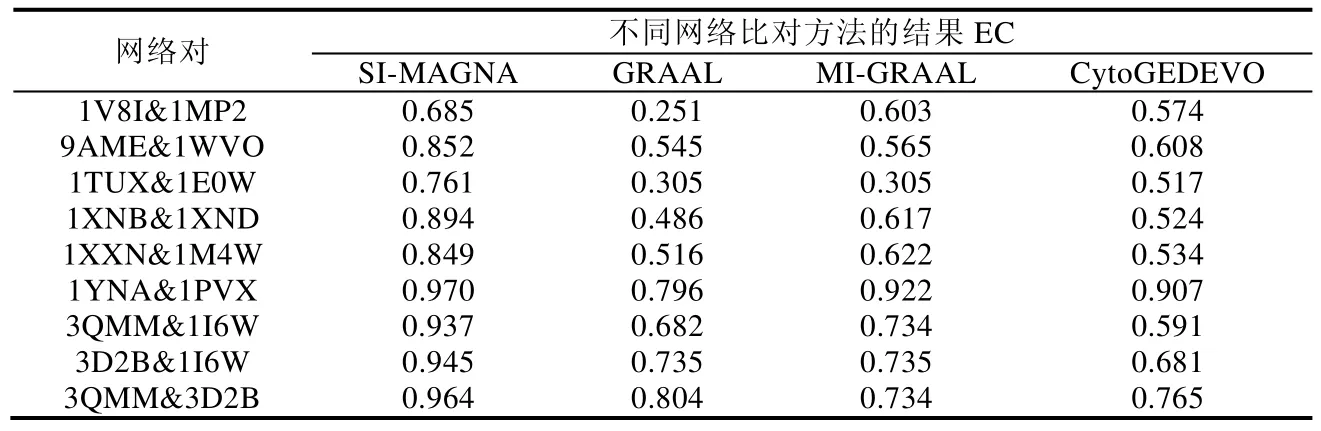
Table 2 Residue interaction network alignment results with different algorithms表2 不同方法下残基相互作用网络的比对结果

Fig.6 Residue interaction network alignment results (EC)with different algorithms图6 不同方法下的残基相互作用网络比对结果(EC)

2.3 SI-MAGNA方法的应用

为了探究蛋白质空间结构与热稳定性的联系[19-22],本文构建了一系列的残基相互作用网络,利用SI-MAGNA 方法进行比对和分析.通过残基相互作用网络比对,发现残基相互作用网络中节点和边的匹配,寻找相似的子结构(共同保守子图).残基相互作用网络对的基本信息和比对结果见表3.

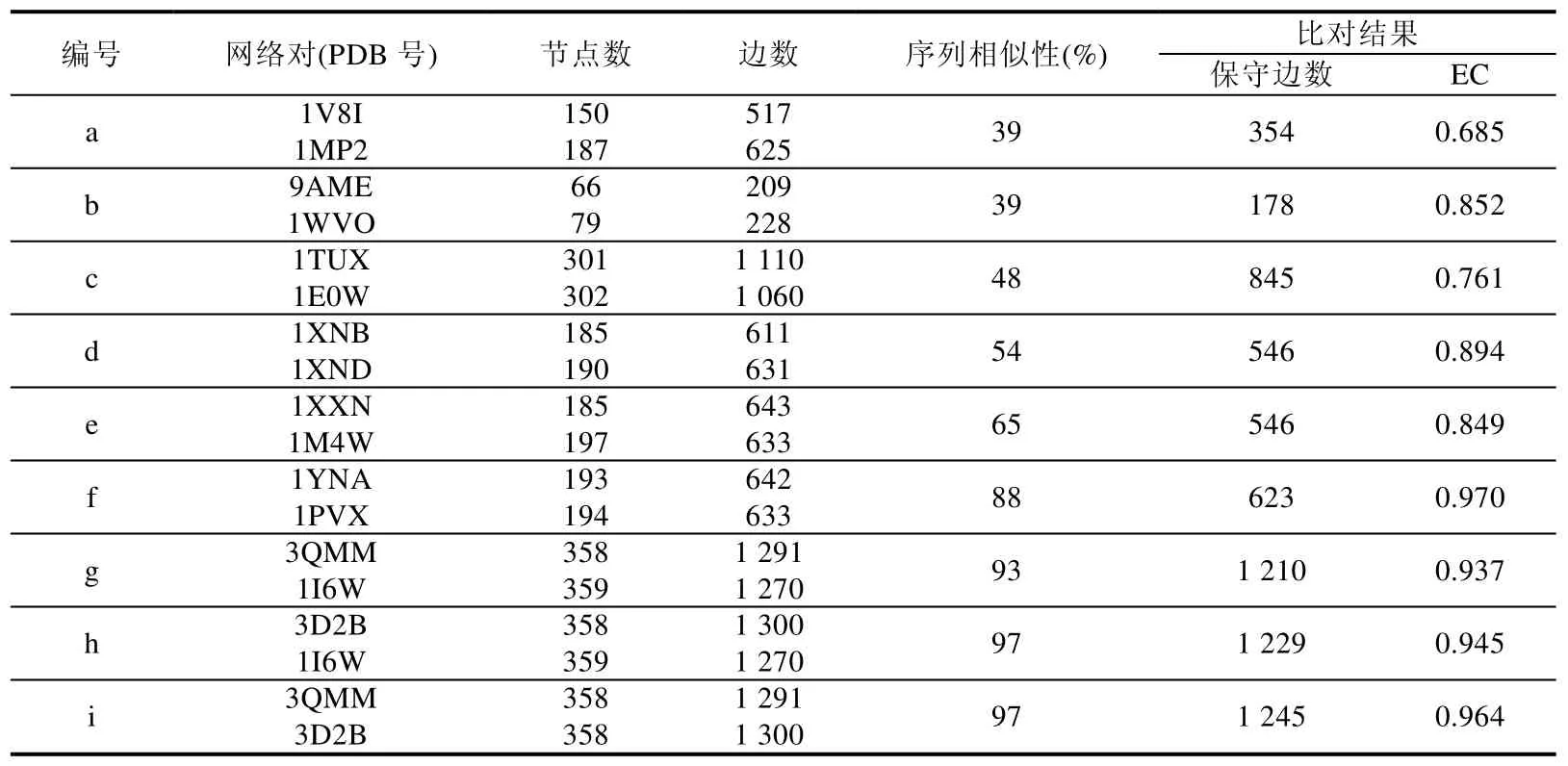
Table 3 Information and SI-MAGNA alignment results of different residue interaction networks表3 不同网络的基本信息和比对结果

使用CytoScape(http://www.cytoscape.org/)软件对SI-MAGNA 方法产生的比对结果进行进一步处理分析,结果如图7 所示,图中各组网络对分别为:(a)1V8I(上左)、1MP2(上右)和两者比对的共同保守子图(下);(b)9AME&1WVO(上右)和两者比对的共同保守子图(下);(c)1TUX(上左)、1E0W(上右)和两者比对的共同保守子图(下);(d)1XNB(上左)1XND(上右)和两者比对的共同保守子图(下);(e)1XXN(上左)1M4W(上右)和两者比对的共同保守子图(下);(f)1YNA(上左)1PVX(上右)和两者比对的共同保守子图(下);(g)3QMM(上左)1I6W(上右)和两者比对的共同保守子图(下);(h)3D2B(上左)1I6W(上右)和两者比对的共同保守子图(下);(i)3QMM(上左)3D2B(上右)和两者比对的共同保守子图(下).在图7 每一组比对中,上方左右两个残基相互作用网络分别代表比对的残基相互作用网络对G1和G2;下方一个残基相互作用网络为比对发现的子结构(共同保守子图),其中,节点表示为xi=yj,xi∈Vi,yj∈V2.这说明在比对中,节点xi和yj相匹配,边表示比对中的保守边.通过比较可以发现两个源网络与比对产生的子结构(共同保守子图)之间的异同,相似性高的部分通常对应于实现相似蛋白质功能的重要区域,而产生差异的部分则有很大的可能是蛋白质性质(如热稳定性)产生差异的原因.

以表3 中b 组比对9AME 和1WVO 为例,其与其余8 组网络对相比较.尽管9AME 和1WVO 的序列相似性不高(39%),但通过残基相互作用网络比对发现,两者空间结构相似性很高,残基相互作用网络比对的EC 达到85.2%,且两者在各自生物体中实现相似功能.这也为“蛋白质的功能由序列信息和特定空间结构共同决定”[12]提供依据.来自高纬度温带海域鱼类的III 型抗冻蛋白质异构体9AME 和来自人类的唾液酸合成酶AFL 结构1WVO 为两种生物的同源蛋白质,在各自生物体中实现非常相似的功能(抗冻蛋白).9AME 的最适反应温度为273K,1WVO 的最适反应温度为293K～310K,两者在稳定性和活性方面具有不同的温度依赖性[23].为了了解两者网络结构的异同,对网络比对发现的子结构(共同保守子图)和二级结构相对应进行标记,如图8 所示,其中,黄色标记的节点表示两源网络匹配上的α-螺旋,橙色标记的节点表示两源网络匹配上的β-折叠,紫色标记的节点表示两源网络匹配上的310-螺旋,棕色标记的节点表示两源网络匹配上的β-桥,蓝色标记的节点表示两源网络匹配上的弯曲,青色标记的节点表示两源网络匹配上的氢键转折,绿色标记的节点表示9AME 中独有的1 个310-螺旋.通过残基相互作用网络比对发现,两者的结构均主要由1 个α-螺旋(9AME 中为残基37-40,1WVO 中为残基41-44)、2 个310-螺旋(9AME 中为残基19-21,57-59,1WVO 中为残基23-25,61-63)和2 个β-折叠(9AME 中为残基4-7,22-25,1WVO 中为残基8-11,26-29)组成,此外,两者均包含一些β-桥和弯曲结构.同时,9AME 中还独有1个310-螺旋(残基34-36)结构,而在1WVO 中,无二级结构相同的结构与之匹配.根据残基相互作用网络比对结果,使用PyMOL(https://pymol.org/2/)软件进一步对9AME 和1WVO 的序列和二级结构图进行标记,这能够更直观地对照和分析两者在序列信息和空间结构上的异同,如图9 所示,其中,黄色标记的序列和二级结构表示两源网络匹配上的α-螺旋,橙色标记的序列和二级结构表示两源网络匹配上的β-折叠,紫色标记的序列和二级结构表示两源网络匹配上的310-螺旋,棕色标记的序列和二级结构表示两源网络匹配上的β-桥,蓝色标记的序列和二级结构表示两源网络匹配上的弯曲,青色标记的序列和二级结构表示两源网络匹配上的氢键转折,绿色标记的序列和二级结构表示9AME 中独有的1 个310-螺旋.

Fig.7 Common conserved subgraph by SI-MAGNA alignment algorithm图7 SI-MAGNA 网络比对方法产生的共同保守子图

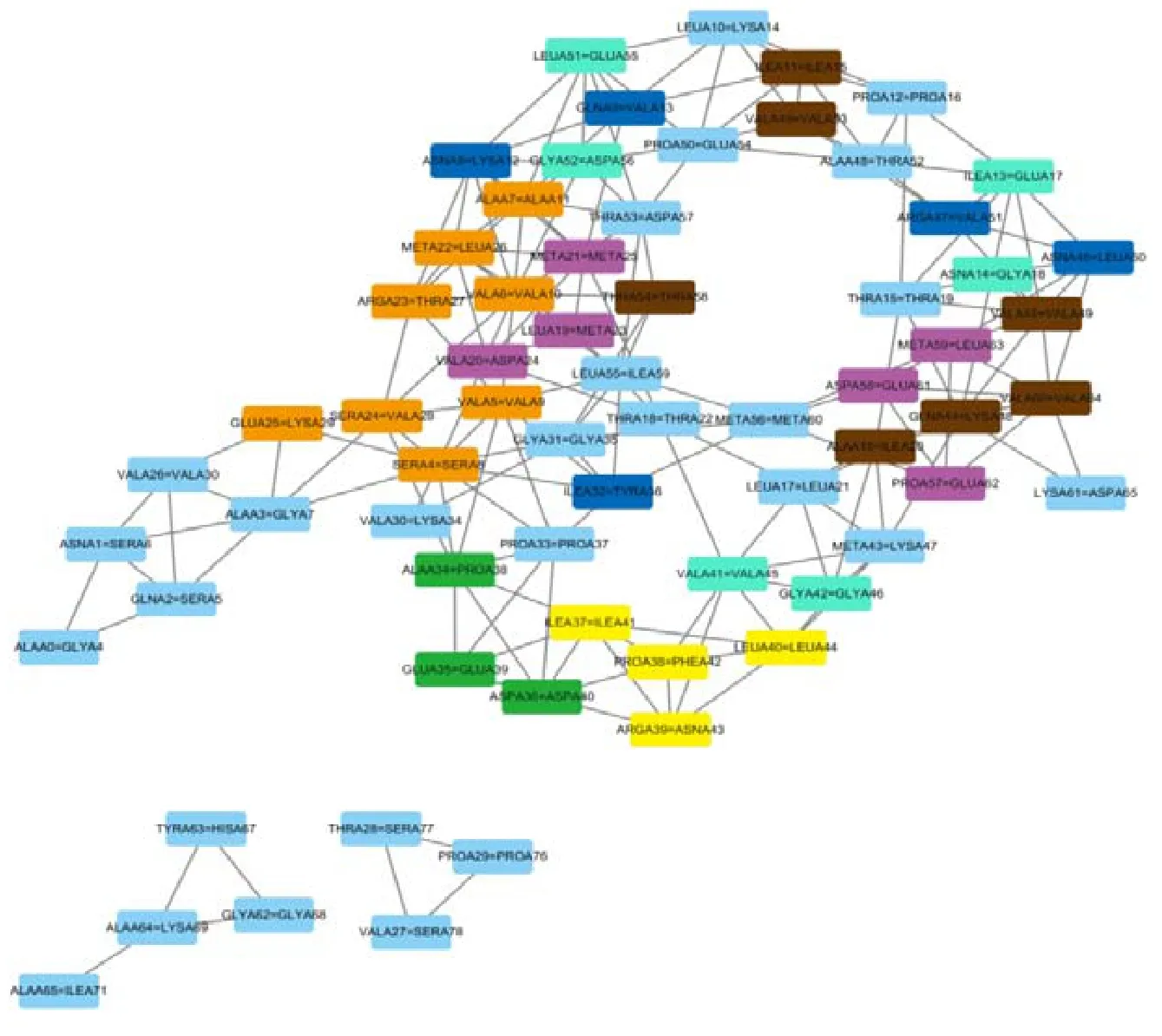
Fig.8 Common conserved subgraph of the 9AME&1WVO by SI-MAGNA alignment algorithm图8 SI-MAGNA 方法发现9AME&1WVO 的共同保守子图

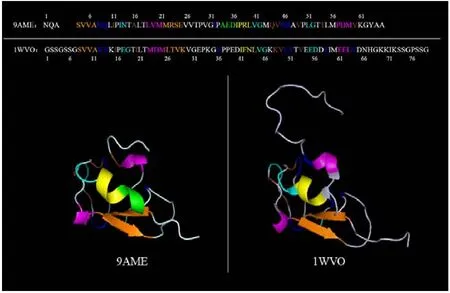
Fig.9 Illustration of sequence and secondary structure of the 9AME&1WVO图9 9AME&1WVO 的序列和二级结构对照图

从图9 中可以发现,9AME 和1WVO 构成相同二级结构的序列相似性很低,但两者主要的二级结构却非常相似.因此可以推断,尽管形成这些特定结构的残基有所不同,但两者共同包含的重要结构(1 个α-螺旋、2 个310-螺旋和2 个β-折叠)以及这些结构间的重要相互作用与两者在各自生物体中实现类似的功能具有极大的关系[24-25],可以从这部分的重要残基及其与周围结构间的重要相互作用入手,进一步探讨实现抗冻蛋白功能的结构.9AME 中独有的1 个310-螺旋结构以及它与周围结构间的重要相互作用,可能是导致两者在稳定性和活性方面具有不同温度依赖性的原因[26],因此可以从这部分的重要残基切入,从结构的角度进一步研究热稳定性产生差异的根源.

3 结果与讨论

针对残基相互作用网络比对,对蛋白质-蛋白质相互作用网络比对算法MAGNA 进行了改进,在其优化函数中引入了蛋白质的序列信息(即残基匹配度),并探讨拓扑信息和序列信息对网路比对的影响程度,使改进的SI-MAGNA 算法更加适用于残基相互作用网络的比对.与此同时,通过实验证实,SI-MAGNA 方法在残基相互作用网络比对方面的表现是优秀且稳定的,并且优于现有的基于网络拓扑的经典网络比对方法.此外,构建了同源蛋白质的残基相互作用网络,使用SI-MAGNA 方法进行网络比对和分析,探索蛋白质结构对蛋白质性质、功能的影响.

残基相互作用网络比对方法将会成为研究蛋白质的空间结构、性质和功能的重要工具.通过残基相互作用网络比对方法进行比对分析,解释蛋白质结构的形成机理、探究蛋白质结构-功能关系,并可以将其运用于分子设计、分子筛选、药物设计等诸多领域.