基于偏置比例导引的垂直攻击滑模制导律
2019-12-11穆忠伟韩秀枫
穆忠伟,吴 剑,韩秀枫
(南昌航空大学信息工程学院,南昌 330063)
0 引言
导弹自第二次世界大战问世以来,受到各国普遍重视,得到很快发展。导弹的使用,增大了战争的突然性和破坏性,扩大了战争的规模和范围,且加快了战争进程,从而改变了过去常规战争的时空观念,给现代战争的战略战术带来巨大而深远的影响[1]。随着精确制导武器的不断改进,除了命中精度这项基本要求外,还需要在命中时刻具有垂直攻击角度,以提高战斗部的毁伤效能。
自从Kim和Grider首次在机动弹头再入制导的研究中引入落角约束问题以来,一些学者根据不同的应用背景及不同的理论方法提出了多种具有终端角度约束的制导律,主要包括最优制导律、滑模变结构制导律、改进的比例制导律以及其他类型的制导律[2-4],并取得了丰富的成果。文献[5]设计了带终端角度约束的变结构制导律,在目标不机动和随机机动的情况下都能满足攻击角度的要求,同时给出了制导律的收敛性证明;文献[6]介绍了一种新导引律的设计方法,改善了弹道特性和制导系统的鲁棒性,但仍无法提供对终端状态的保证;文献[7]针对导弹以一定角度攻击特定目标的问题,提出了基于多项式函数的落角约束制导律方法;文献[8]针对导弹要求限制末端攻击角度的作战要求,基于滑模变结构控制理论,面向机动目标,设计了一种满足脱靶量及攻击角度约束的制导律;文献[9]对弹目相对运动作线性近似后,基于二次型最优控制理论给出了俯冲击顶制导律,但其缺点是需要估计剩余时间,以及求解比较复杂的微分方程两边的边值问题;文献[10]针对远距离拦截高速、大机动目标的拦截弧度长的问题,在满足攻击角度的约束条件下,通过引入分段线性和指数两种形式的阻尼,使得导弹在拦截高速高加速目标时,对目标机动的敏感度随弹目距离变化,从而达到能量管理的目的;文献[11]针对临近空间高超声速巡航飞行器拦截所面临的制导策略,提出了采用高抛弹道拦截的设计方法。
本文针对空地导弹攻击地面固定目标的问题,在传统的比例导引律的基础上,增加了一个角度偏置项,并结合滑模变结构的控制理论,设计了一种新型垂直攻击目标的制导律。该制导律克服了终端角度无法约束的问题,并详细地对比了其与传统比例制导律在攻击地面目标时的不同,验证了本文中所设计制导律的优越性能。
1 弹目相对运动建模与分析
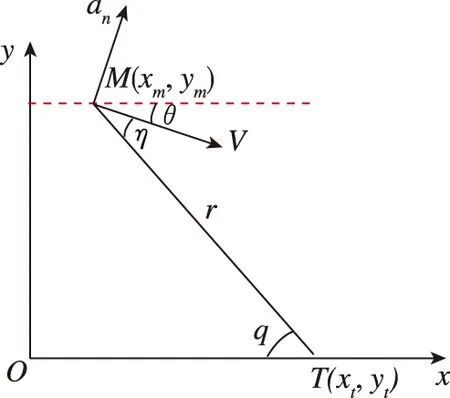
图1 导弹-目标相对运动关系Fig.1 Missile-target relativemotion relation
根据导弹与目标的相对关系得出了相对运动方程为
(1)
2 导引律设计
2.1 导引律推导
由于末制导段多采用响应速度较快的过载驾驶仪,常以法向加速度指令作为指令信号,因此假定导弹采用具有如下结构的偏置比例导引的制导律形式为
(2)
式中,K≥2,u为偏置项。
对式(1)第二项求导可得
(3)
进而可得
(4)

(5)
2.2 自适应垂直攻击结构项的设计
要保证导弹最终以期望角度攻击目标,并以零化视线角速度完成攻击任务,令
x1=q(t)-qf
(6)
(7)
式(6)中,qf为落点处的期望视线角度。若使状态x1趋于0,则可实现以期望的攻击角度接近目标的任务;若使状态x2趋于0,则能够以保持固定的角度攻击目标,提高了击中目标的性能。
式(6)、式(7)的终端约束条件为
首先需要选择设计一个滑模切换平面,以迫使系统在一定特性下沿规定的状态轨迹做小幅度、高频率的上下运动,即滑模运动。为了在制导过程中使状态x1和x2逐渐趋于0,同时满足零化脱靶量和末端落角的要求,故设计切换函数[14]为
S=x2+λVx1/r
(8)
其中,λ为大于0的常数。当S=0时,系统处于滑模运动状态,此时x1=x2=0,导弹可以按照期望落角命中目标。
当系统在有限时间内到达切换平面后进入滑动模态,系统要满足可达性条件
(9)
可达性条件保证了系统运动在有限时间内到达切换平面,但对这段时间内具体的状态轨迹没有约束。为了改善这段运动的动态品质,通过设计趋近律来加以控制。选取具有自适应特性的指数趋近律
(10)
式中:w>0,ε>0。
现将式(8)求导可得
进而
(11)
将式(10)与式(11)联合求得
进而可得
(12)
将式(12)代入式(5)中可得
u=
进而可得
u=
(13)
将式(13)代入可得
(14)
2.3 稳定性分析
应用Lyapunov方法对系统稳定性进行分析。选择Lyapunov函数为
(15)
则有
(16)
即得系统在Lyapunov意义下是渐近稳定的。
2.4 基于连续切换的滑模控制变结构制导律
在滑动模态控制系统中,如果控制结构的切换具有理想的开关特性,则能在切换面上形成理想的滑动模态,这是一种光滑的运动,渐近收敛于原点。但在实际工程应用中,由于存在时间上的延迟和空间上的滞后等原因,使得滑动模态呈现抖振形式,即在光滑的滑动模态上叠加有抖振。抖振问题是影响滑动模态控制的主要问题。
为了削弱抖振,需要引入继电特性连续化的方法代替符号函数sgn(s),实现准滑模动态控制,即在边界层外采用正常的滑模控制,在边界层内采用连续状态反馈控制[16-18],旨在避免或削弱抖振影响
(17)
其中,δ是很小的正常数。将式(17)代入导引律式(14)中得
(18)
可见式(18)基于偏置比例导引的滑模制导律主要由两项组成,第一项为与视线角速度成正比的比例导引项;第二项为根据落角约束确定的滑模变的偏置项。
3 仿真分析
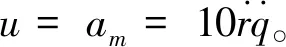
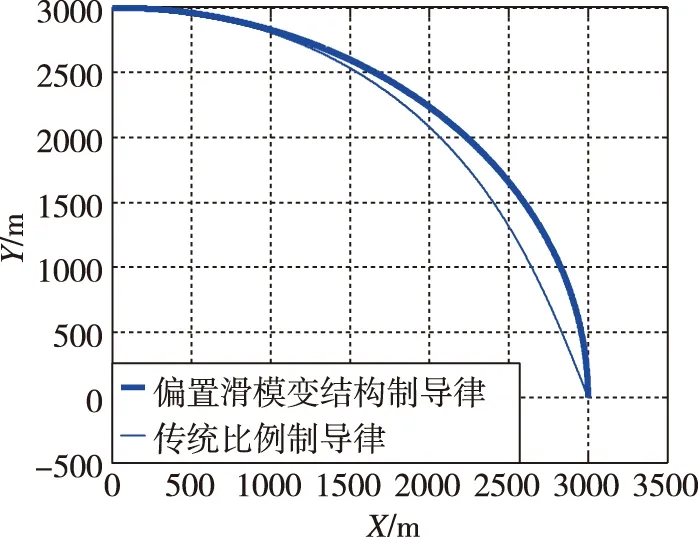
图2 两种制导律的弹道轨迹曲线Fig. 2 Trajectories of two guidance laws
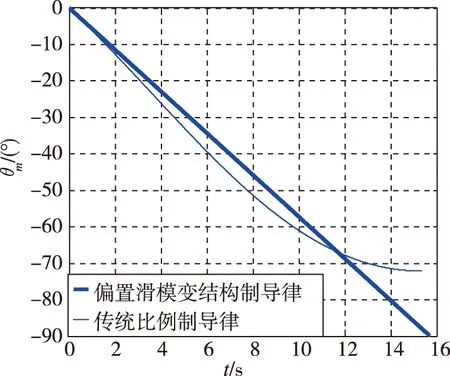
图3 两种制导律的弹道倾角曲线Fig.3 Trajectory inclination angle curves of two guidance laws
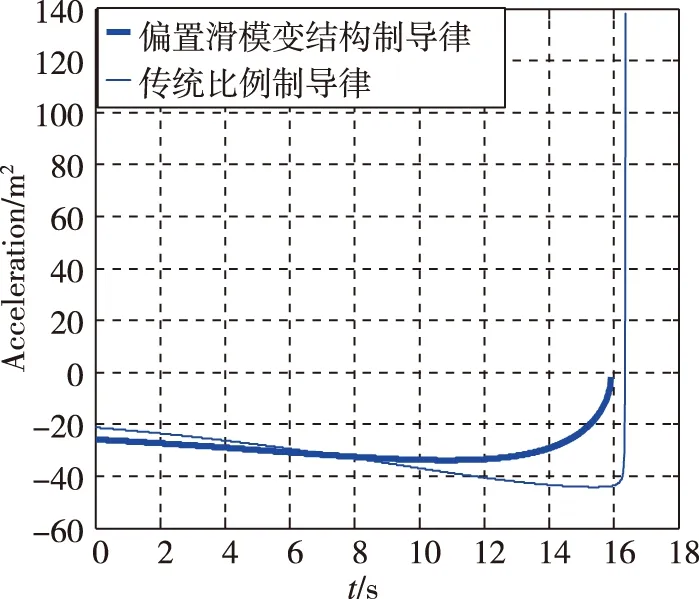
图4 两种制导律的加速度曲线Fig.4 Acceleration curves of two guidance laws
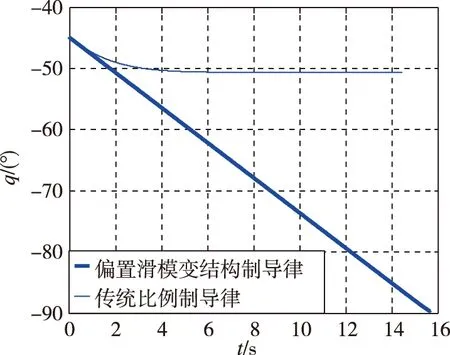
图5 两种制导律的视线角曲线Fig.5 Line of sight of two guidance laws
由表1可以看出,偏置滑模结构制导时间是15.7100,大于比例导引的制导时间15.3300,故带偏置比例导引滑模制导律的制导时间比传统比例导引律的制导时间稍长。这是由于传统比例导引的弹道曲线较低,而偏置滑模结构导引的弹道曲线较高(如图2所示)的缘故。但是这对导弹进行低空突防是非常有利的,尤其是在实际情况中,较高的弹道可以为导弹提供更快的攻击速度,增大毁伤效果。从仿真结果可知,变结构制导律脱靶量更小,具有更高的制导律精度。

表1 两种导引律制导效果的比较
由图4可以看出,在导弹制导过程中,两种方法的加速度都在增大,但偏置变结构制导律的最大过载比传统比例导引律的最大过载要小得多。随后二者过载都开始减小,偏置变结构制导律的过载最后趋向于0,然而传统比例制导律的过载变小,后又再次增大,所以前者的过载趋于零变化,降低了对导弹执行机构的要求,更易于应用在实战中。
结合表1与图3可知,偏置比例的滑模制导律的落角偏差是0.2852,而传统比例导引的落角偏差是17.8966。从中可以看出,偏置比例滑模的方法要比传统导引攻击的角度更加接近90°,几乎以垂直的方式攻击地面目标,提高了攻击目标的毁伤效果;而传统比例导引偏差过大,无法以90°角攻击目标。
4 结束语
本文通过建立纵向平面内弹目相对运动学模型,在传统比例导引律的基础上,利用落角和脱靶量的约束条件,结合滑模变结构理论设计了一个落角约束偏置项,推导得到了满足垂直攻击落角的导弹制导律,并与传统比例导引律进行了对比仿真。通过选取合理的制导律参数,可以使导弹的法向过载在攻击目标的过程中逐渐趋向于0,这是传统比例制导律所不能达到的,并通过仿真验证了该制导律的有效性和优越性。
