十二表冗余捷联惯导系统数据融合技术研究
2019-12-11郭建刚王跃鹏
郭建刚,王跃鹏,郑 伟
(1.国防科技大学空天科学学院,长沙 410073;2.北京航天时代激光导航技术有限责任公司,北京 100094 )
0 引言
基于激光陀螺的激光捷联惯性导航系统作为控制系统的主要设备之一,已成为航天运载火箭、航天飞机、飞船、星际探测、太空站等系统的核心制导控制设备,并广泛应用。其主要工作原理是利用激光陀螺仪及石英加速度计作为惯性敏感部件,实时测量载体姿态和速度等信息,为控制系统导航解算提供依据。相较于平台式惯导系统,捷联式惯导系统具有结构简单、工作寿命长、力学环境适应性强、可靠性高等特点,同时由于其自主性、连续性、隐蔽性等优点,惯性导航系统在组合导航系统中常作为基础参考系统,其可靠性至关重要[1]。
随着现代航空航天技术和需求的进一步发展,对导航系统的可靠性的要求也越来越高。提高导航系统可靠性的系统设计手段主要有多表冗余和多机备份两种方式,其中多表冗余设计以其更低的硬件成本和更高的理论可靠度成为目前国内外研究和应用的主流。例如应用于波音777飞机的容错大气数据参考系统(Fault-Tolerant Air Data Inertial Reference System,FT/ADIRS)和德尔塔系列火箭的冗余激光捷联惯性导航系统(Redun-dant Inertial Flight Control Assembly,RIFCA)[2],均采用了十二表(6只激光陀螺、6只加速度计)冗余设计,理论可靠度与四套常规系统相当。在多表冗余惯导系统工作的过程中实时进行系统的故障诊断与隔离,主要方法有广义似然检验(Generalized Likelihood Test,GLT)[3-4]、最优奇偶性测试(Opti-mal Parity Test,OPT)[5-6]、多奇偶向量法[7]以及双故障隔离法[8]等,之后利用剩余正常仪表完成导航解算。
多表冗余惯导系统数据融合技术是利用冗余仪表数据提高系统导航精度的有效手段。飞行器控制系统完成导航解算需要惯导系统输出的三轴姿态和速度信息,常规三正交惯导系统通过3只陀螺和3只加速度计的输出可直接解算得到上述信息。采用多表冗余设计的惯导系统,由于冗余仪表输出的测量数据存在冗余,彼此不独立,因此可以通过多传感器数据融合技术,利用最优估计算法得到三轴姿态和速度信息的最优估计值,从而尽可能地消除测量数据中的随机误差,充分利用所有测量数据,提高导航精度。
本文针对采用正十二面体构型方案的十二表冗余激光捷联惯性导航系统(以下简称十二表系统),通过仿真计算和实物样机试验测试对系统的数据融合算法进行了研究。
1 正十二面体仪表冗余构型和样机简介
十二表冗余惯导采用6只激光陀螺和6只石英加速度计的冗余配置,在仪表精度一定的情况下,该仪表构型方案直接影响系统的导航精度和故障诊断与隔离的能力。正十二面体仪表冗余构型是激光惯导采用12只惯性仪表配置时的最优仪表构型方案,能够使系统导航性能最优,同时故障检测能力也显著优于其他几种构型方式[9]。
1.1 正十二面体仪表构型简介
常规惯导系统只需配置6只仪表,包括3只陀螺和3只加速度计,以完成对载体的角运动和线运动共6自由度运动信息的测量,仪表采用正交配置,且各仪表敏感轴与惯导测量坐标系各坐标轴重合,如图1所示。其中O-X1Y1Z1为箭体坐标系,其中OX1为纵轴,OY1为法向轴,OZ1为横向轴;O-XsYsZs为激光惯导测量坐标系,与箭体坐标系重合;Gx、Gy、Gz和Ax、Ay、Az分别为3个激光陀螺和3个加速度计,安装方向与OXs、OYs、OZs轴方向一致。
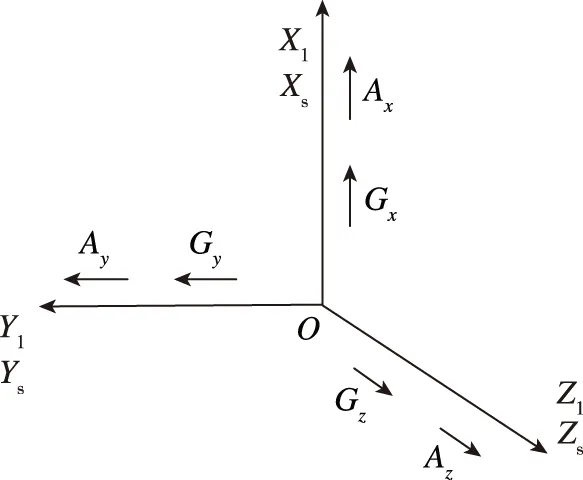
图1 惯性仪表安装定向示意图Fig.1 Installation orientation of inertial instruments
正十二面体的12个表面均为正五边形,且两两平行。仪表敏感轴线与各面法线一致,且对应的陀螺和加速度计配置在相互平行的一对表面上。 正十二面体仪表冗余构型方案的系统测量矩阵如式(1)所示,仪表配置角度如图2所示。
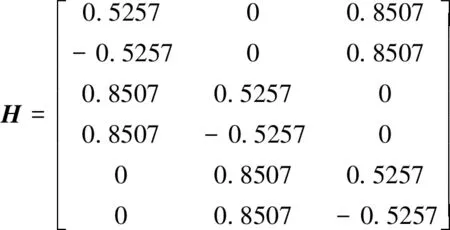
(1)
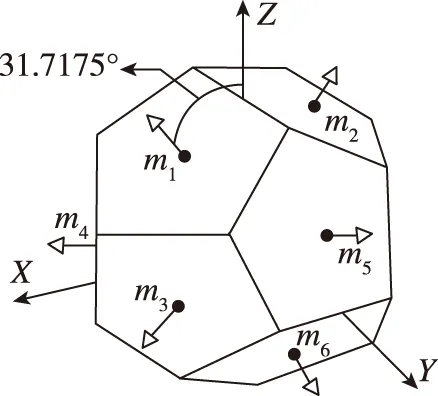
图2 正十二面体构型方案Fig.2 Redundant configuration of dodecahedron
多表冗余惯导系统导航性能最优的充分必要条件是系统测量矩阵H满足式(2),其中n是陀螺或者加速度计的个数[9-10],十二表冗余惯导系统n=6。同时在综合考虑导航性能及FDI性能两项指标的情况下,正十二面体方案为十二表冗余配置的最优配置方案。
(2)
1.2 基于正十二面体仪表构型的激光惯导样机设计
基于正十二面体仪表构型,设计并制造了惯导样机,其中惯性测量单元(Inertial Measurement Unit,IMU)集成安装了激光陀螺和石英加速度计,是激光惯导的核心部分。所制造的样机及IMU分别如图3和图4所示。

图3 十二表冗余激光惯导样机Fig.3 Prototype of the 12-sensor redundant SINS

图4 惯性测量单元Fig.4 IMU
IMU采用八点式内减振设计,仪表选用6只北京航天时代激光导航技术有限责任公司设计生产的50型一体化机抖式激光陀螺(陀螺精度优于0.01(°)/h)和6只高精度加速度计。
2 基于最小二乘估计的数据融合算法
最小二乘估计(Least Square Estimation, LSE)是高斯(Karl Gauss)在1795年为测定行星轨道而提出的参数估计算法。这种估计的特点是算法简单,不必知道与被估计量及量测量有关的任何统计信息[11]。最小二乘估计至今仍是工程领域十分常用也非常有效的一种最优估计算法。美国国家航空航天局(National Aeronautics and Space Administration,NASA)的空间惯性参考单元(Space Inertial Reference Unit,SIRU)项目使用加权最小二乘算法进行冗余仪表的数据融合[12]。
2.1 十二表系统数据处理流程
十二表系统在导航解算过程中的数据处理流程是:首先搭载在飞行器上的惯导系统在飞行器发射和飞行过程中,各冗余仪表以一定的采样周期实时输出动态测量信息;然后根据冗余仪表输出,通过数据融合技术获得飞行器三轴角增量Δθ和速度增量ΔV;然后通过自对准获得飞行器初始姿态;最后进行导航解算获得飞行器实时位置和姿态信息。主要数据处理流程如图5所示。
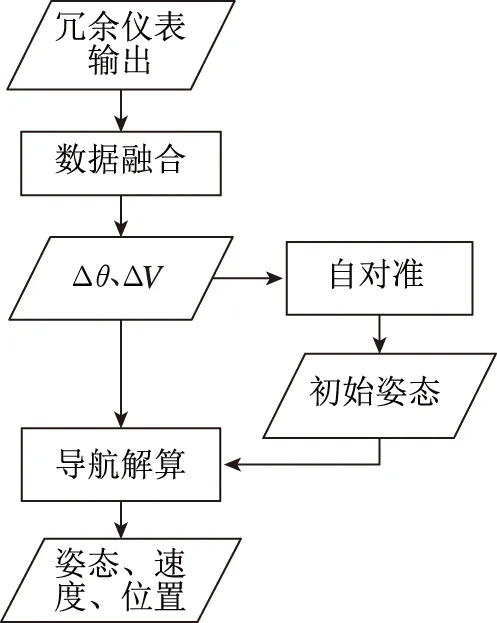
图5 数据处理流程Fig.5 Data processing flow
2.2 基于最小二乘的数据融合算法
对于测量系统
Zm=Hm×nXn+Vm
(3)
其中,Xn为n维状态矢量;Zm为m维量测量;Hm×n为量测矩阵,m>n;Vm为测量噪声,其均值为0,方差阵为R。Xn的最小二乘估计为
一般情况下最小二乘估计的精度不高,原因之一是其不分优劣地使用了所有测量值,特别是当多组测量数据中某组数据精度显著低于其他数据时,最小二乘的估计效果甚至不如只使用其中一组高精度测量值时好。当对不同测量值的质量有所了解,可根据其精度质量通过加权的方法进行区别对待,能够有效提高估计精度。式(3)中Xn的加权最小二乘(Weighted Least Squares Estimator, WLSE)估计为
其中,W为适当取值的正定加权矩阵。
如果取W=R-1,则称为马尔柯夫估计,马尔柯夫估计的均方误差比任何其他加权最小二乘估计的均方误差都要小。
十二表系统测量方程可以简化表示为
(4)
其中,Ng和Na分别为陀螺和加速度计的测量输出;Kg和Ka分别为陀螺和加速度计的当量;Dg和Da分别为陀螺和加速度计零偏;dt为系统采样时间间隔;Hg和Ha分别为陀螺和加速度计的测量矩阵;Vg和Va分别为陀螺和加速度计的测量噪声,且均值为0,方差阵分别为Rg和Ra。
则,Δθ和ΔV的最小二乘估计为
(5)
Δθ和ΔV的加权最小二乘估计为
(6)
Δθ和ΔV的马尔柯夫估计为
(7)
2.3 十二表系统最小二乘估计的精度分析
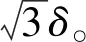
对于采用仪表冗余设计的十二表系统,系统冗余度为6,采用直接对比法最多可以诊断和隔离2度故障,采用解析冗余算法最多可以诊断和隔离3度故障。因此对于十二表系统,以姿态解算为例,只要发生故障的陀螺不大于3只,系统就能完成姿态导航解算。当故障仪表数量增加时,一方面系统测量信息减少,另一方面系统测量矩阵恶化,这将导致系统精度的恶化。因此,当某只仪表发生故障时,根据其安装位置或测量向量,特定坐标轴上(精度最差轴)的精度损失更大。因此对系统故障陀螺或加速度计数量分别为0只、1只、2只和3只时系统的精度情况进行分析,结果如表1所示。
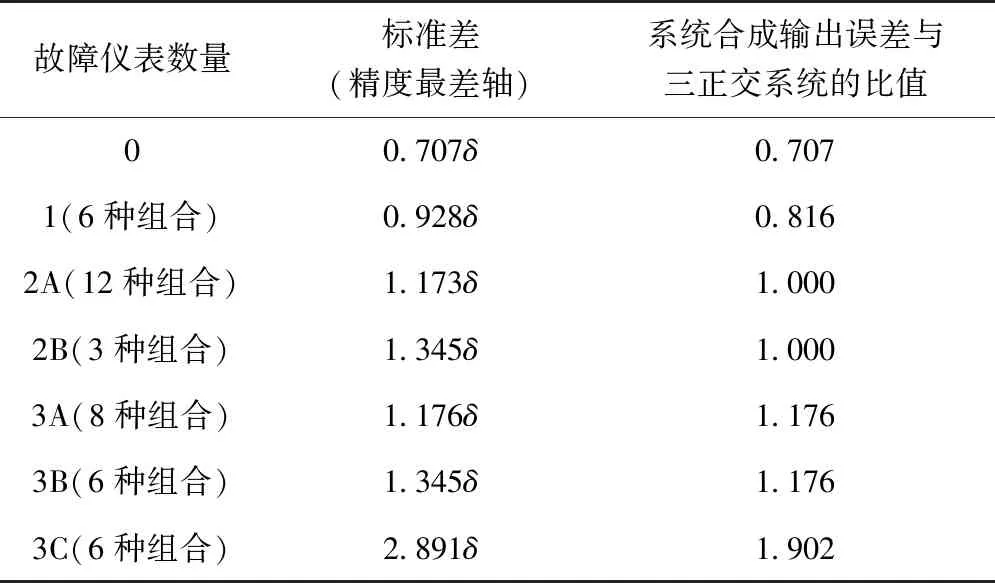
表1 不同故障模式下系统精度表现
从表1中可以看出,随着故障仪表数量的增加,系统合成输出误差逐渐增大,当系统无故障或只有1只仪表故障时,系统精度显著优于同精度仪表构成的三正交系统。不同故障模式下,各轴输出精度差异明显,极端模式下只有2只仪表故障(2B)时单轴输出精度甚至比3只仪表故障(3A)更低。但整体上,除极少数情况(3C)外,系统精度均优于三正交系统或与之相当。
3 数据融合算法的Monte Carlo仿真
为验证基于最小二乘估计的数据融合算法的有效性,编写了Matlab仿真计算程序,模拟十二表系统静态导航试验,并在仪表输出中加入白噪声以反映仪表测量误差情况。设计了四组对比仿真,如下:
第一组,使用如图2所示的m1、m3、m5这3只仪表的数据,无需数据融合直接解算,这种仪表选择也是正十二面体构型中精度最高的三表组合方式[13];
第二组,使用六表数据和最小二乘估计的数据融合算法,第一、二组仿真中各仪表精度相同,并且在一次Monte Carlo打靶中使用同一组仿真数据;
第三组,同样使用六表数据和最小二乘估计的数据融合算法;
第四组,使用六表数据和马尔柯夫估计的数据融合算法,第三、四组仿真中提高m3陀螺/加速度计的噪声方差,其余仪表精度相同且与第一、二组仿真一致,第三、四组仿真在一次Monte Carlo打靶中使用同一组仿真数据。
每组进行500次Monte Carlo打靶,统计导航结果中位置误差和姿态误差的均值,如表2所示。从表2仿真结果中可以看出,当各仪表精度相同时,使用最小二乘估计的数据融合算法能够有效降低系统导航的位置误差和姿态误差;但当各仪表精度不完全一致时,最小二乘估计的数据融合质量显著下降,此时使用马尔柯夫估计根据各仪表输出数据的噪声方差情况对冗余仪表数据进行加权,完成数据融合之后,仍能有效降低系统导航误差,且位置和姿态误差显著优于三表直接解算。
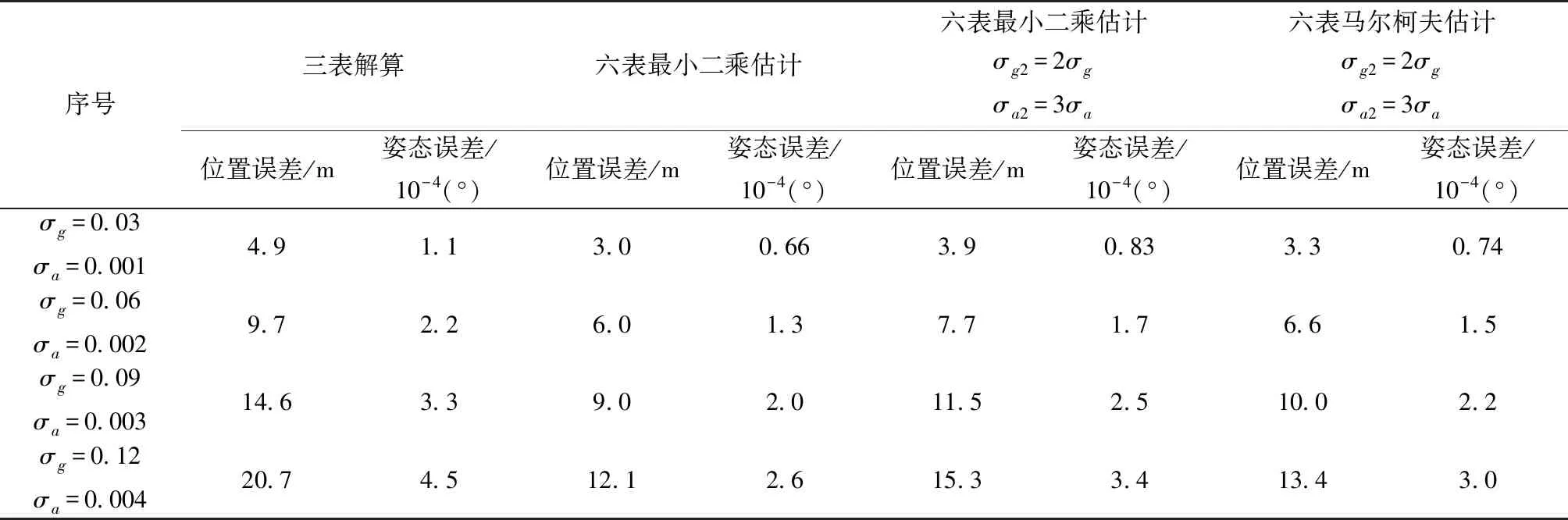
表2 不同数据融合算法的Monte Carlo仿真结果
上述仿真计算验证了使用最小二乘估计进行数据融合对提高多表冗余惯导系统导航精度的有效性。同时由于实际工程应用中各仪表精度并不完全一致,因此如何评价和加权使用各表数据输出,是提高基于最小二乘估计的数据融合算法性能的关键。
4 基于样机静态导航试验的数据融合算法测试
基于所制造的十二表系统实物样机,开展了静态导航试验,对基于最小二乘估计的数据融合算法的性能进行了测试。
样机静态导航试验的流程是,首先通过标定获得系统诸元;然后将样机放置在大理石平板进行静态数据采集,存储各仪表输出;最后使用离线程序,根据如图4所示的数据处理流程,完成导航解算,获得静态导航的位置和姿态误差。静态导航试验进行了6组,每组数据长度15min,其中前5min数据用于完成系统自对准,后10min数据用于导航解算,采样间隔5ms。
对每组试验数据分别进行三表直接解算(仪表选择方案与仿真相同)、六表采用最小二乘估计进行数据融合和六表采用马尔柯夫估计进行数据融合,三种不同方式获得的系统三轴角增量Δθ和速度增量ΔV,最终导航误差结果如表3所示。其中第一组试验数据采用不同数据融合方式的导航误差曲线如图6~图8所示。从结果中可以看出,由于样机各表精度情况相差较大,因此采用最小二乘估计的方法进行数据融合之后,样机的导航误差显著大于三表直接解算;而采用马尔柯夫估计的数据融合算法,最终样机导航误差比最小二乘估计的数据融合算法略有降低,但仍显著大于三表直接解算。
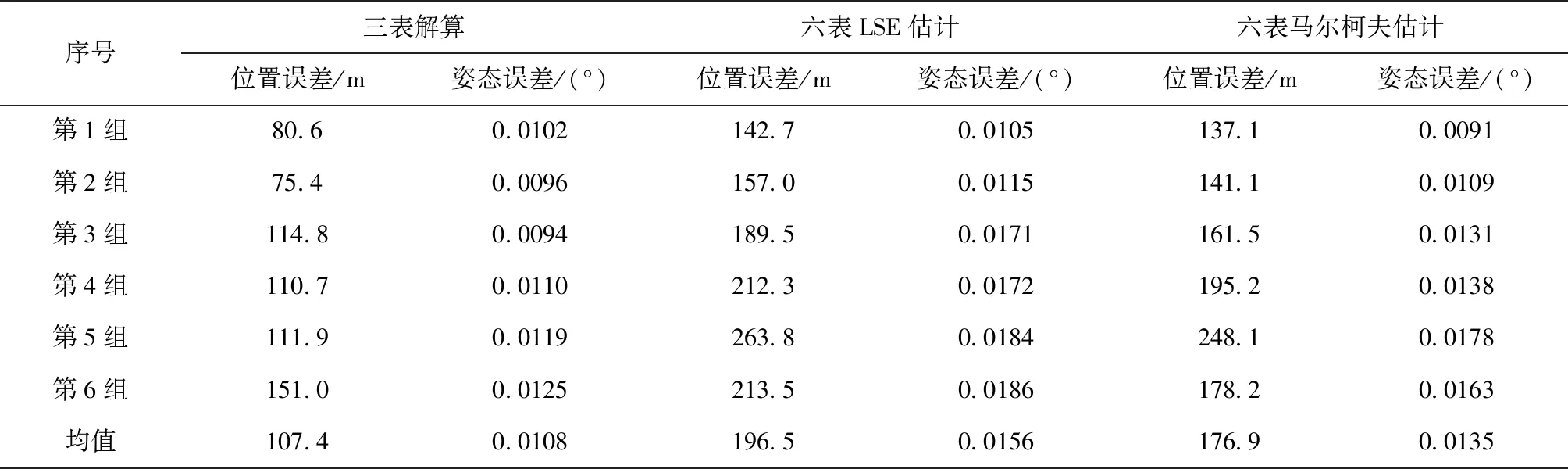
表3 不同数据融合算法的静态导航试验结果
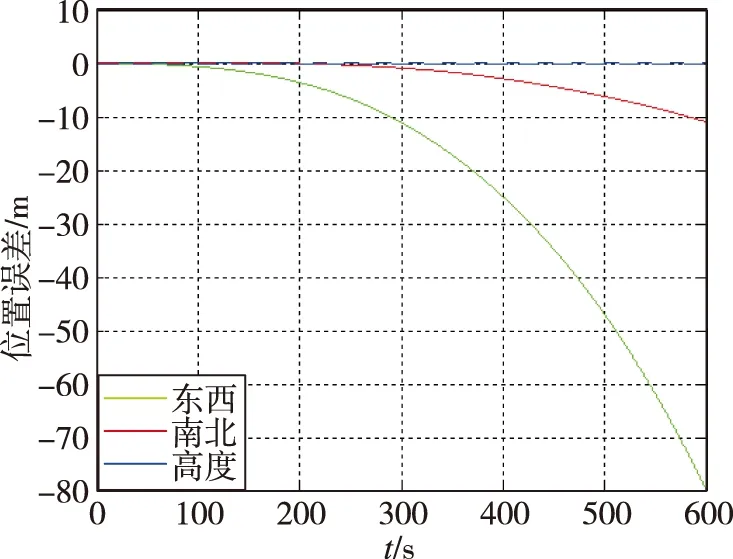
(a)位置误差
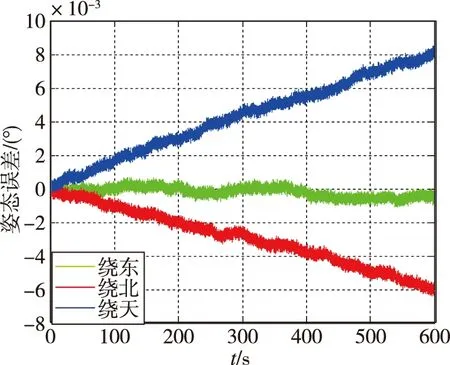
(b)姿态误差
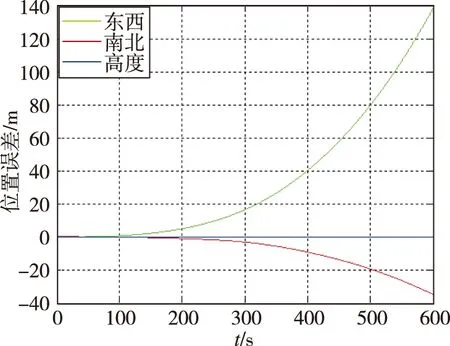
(a)位置误差
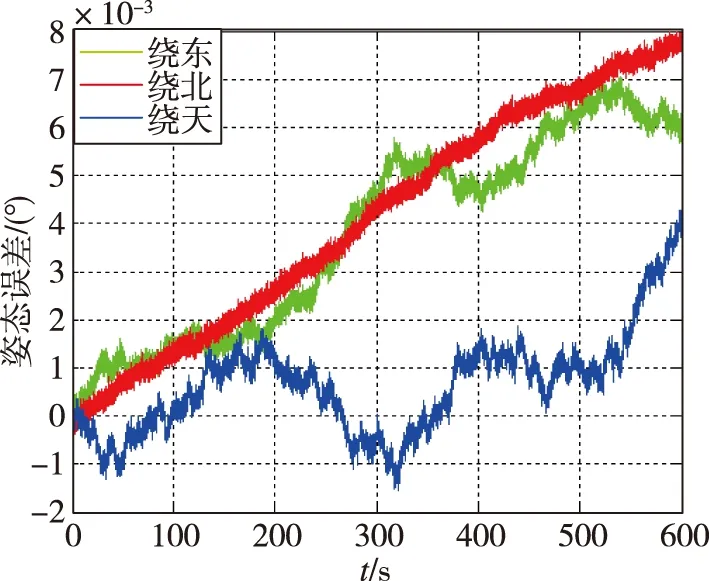
(b)姿态误差
(a)位置误差
(b)姿态误差
5 加权系数的优化改进
上述试验结果显示,采用马尔柯夫估计数据融合算法的导航精度没有明显改善,与理论和前述仿真结果矛盾。对仪表的输出数据进行仔细分析发现,由于所选用陀螺和加速度计均为积分仪表和脉冲输出的形式,其在一个采样周期内只有累加到足够(一个当量)的角增量或者速度增量,才会有脉冲输出,否则累加到下一个采样周期。而静态导航下仪表只敏感到地球重力加速度和自转角速度且采样周期只有5ms,导致一个采样周期内仪表没有足够输出。试验中仪表的一段输出数据如表4所示,其中A1~A6为加速度计的输出,G1~G6为陀螺输出。从表4中可以看出,仪表原始输出受采样影响明显,因此对仪表数据直接取方差时并不能代表仪表的真实噪声水平和数据质量,这是导致马尔柯夫估计失效的原因。
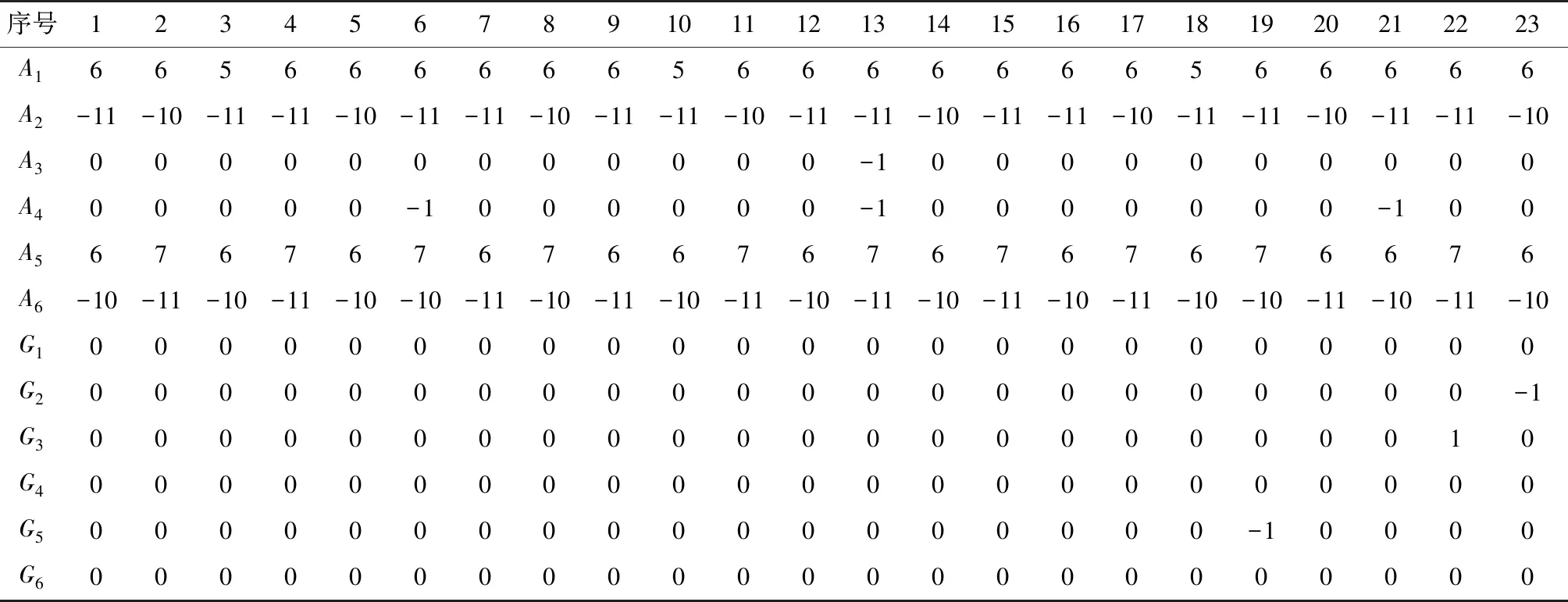
表4 仪表5ms脉冲增量输出
在惯性导航中,影响导航精度的仪表参数主要是陀螺的零偏稳定性、加速度计的零偏稳定性和当量误差,其中仪表的零偏稳定性比较容易准确获得。因此选择各仪表零偏稳定性参数作为加权系数,构造加权矩阵如式(8)所示,其中Ω1,…,Ω6为6只陀螺或加速度计的零偏稳定性。
(8)
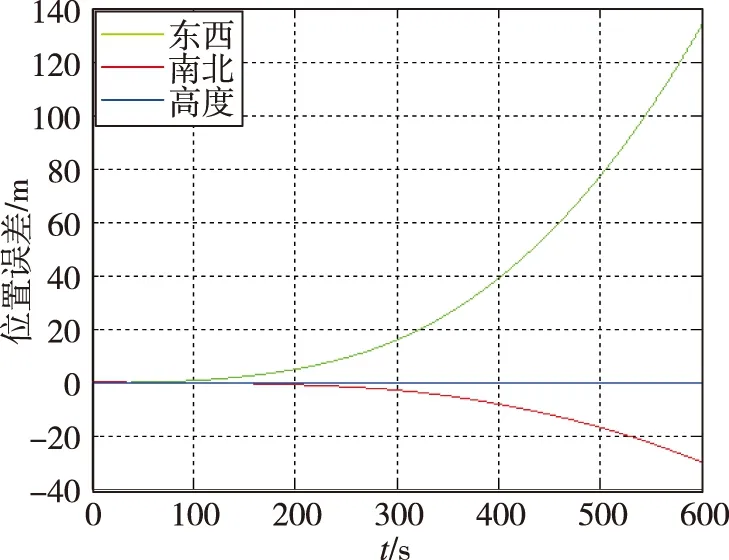
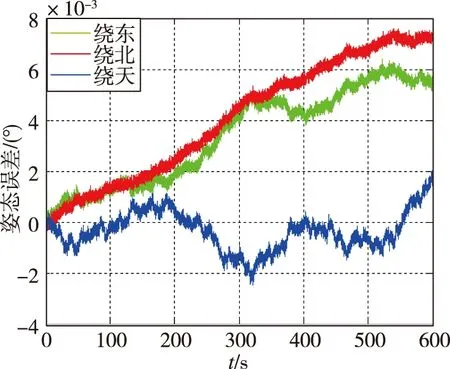
使用构造的加权矩阵,根据式(6)完成数据融合,重新对6组样机静态导航试验数据进行处理,得到系统导航误差,如表5所示,其中第一组数据的导航误差曲线如图9所示。从结果中可以看出,优化加权系数后样机的导航精度显著提升,六组静态导航试验数据的平均位置误差和姿态误差分别只有23.0m和0.0024°,与三表直接解算相比位置误差和姿态误差分别降低了78.6%和77.9%,且与由3只90型高精度激光陀螺(精度优于0.005(°)/h)和3只同型高精度加速度计组成的三正交惯导系统的导航精度相当。
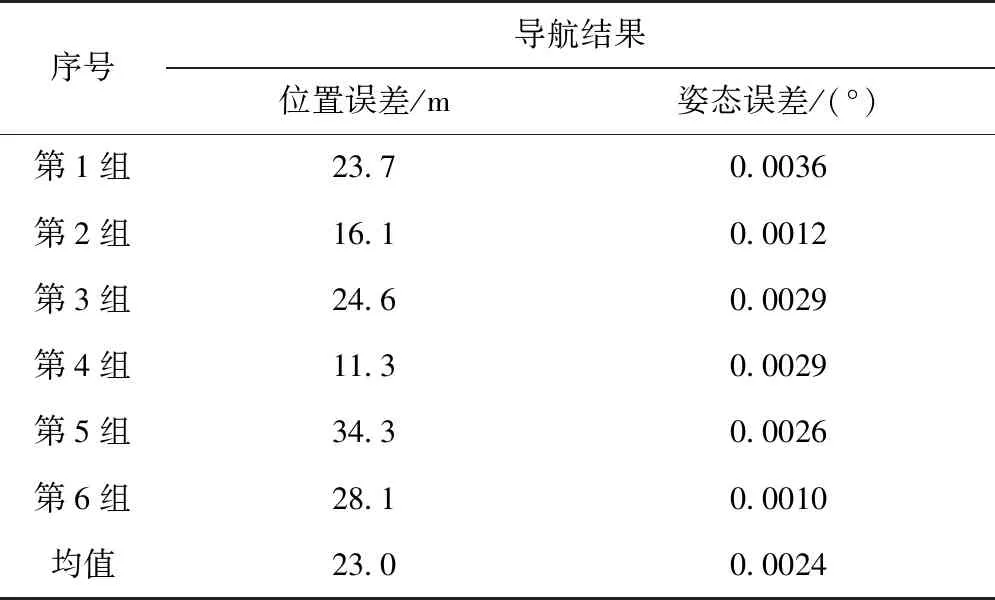
表5 优化加权系数的WLSE数据融合算法的样机静态导航试验结果
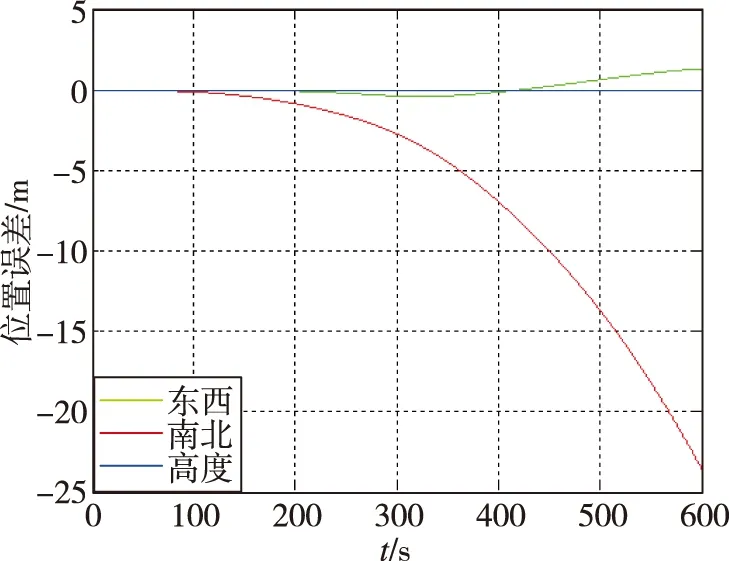
(a)位置误差
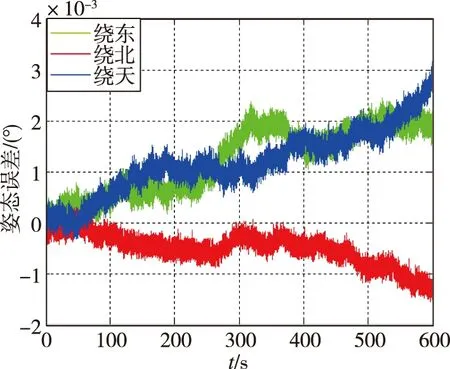
(b)姿态误差
6 结论
多表冗余惯性导航系统可以通过数据融合技术,充分利用冗余仪表的数据,达到提高系统的导航精度的目的。本文针对采用正十二面体冗余仪表构型的十二表冗余激光捷联惯性导航系统,通过仿真和样机试验,开展了基于最小二乘估计的数据融合算法研究;分析了不同故障模式下的系统精度变化,并通过Monte Carlo仿真验证了数据融合算法对提高系统导航精度的有效性;设计开展了样机静态导航试验,试验结果表明,理论最优的马尔柯夫估计并不完全适用于脉冲输出形式仪表的数据融合;最后通过优化改进加权系数和构造加权矩阵,显著提升了样机的静态导航精度:样机位置误差和姿态误差与三表直接解算相比分别降低了78.6%和77.9%。6组试验的平均误差只有23.0m和0.0024°,这与由3只90型高精度激光陀螺和3只同型高精度加速度计组成的三正交惯导系统的导航精度相当。
