具有恶化效应与可控加工时间的工期指派排序问题研究
2019-12-10王吉波刘巍巍
王吉波,张 博,刘巍巍
(1.沈阳航空航天大学 理学院,沈阳 110136;2.沈阳体育学院,管理与新闻传播学院,沈阳 110102;3.东北大学,计算机科学与工程学院,沈阳 110169)


1 提出描述
设有n个工件J1,J2,,Jn要在一台机器上加工,工件在加工过程中不可中断,所有工件零时刻到达。本文研究工件的加工时间是消耗资源的线性函数的模型,即假定工件Ji的实际加工时间为
(1)

和
2 主要结论
引理1(WEI等[15],WANG等[16])对于给定的排序π=[π(1),,π(n)],工件π(i)的完成时间和实际加工时间分别是:
(2)
和
(3)

证明:与文献BRUCKER[20]和LIU等[21]中的证明方法类似。
假设一个虚拟的任务J0,其权重是ω0,处理时间是p0=0(任务J0在0时刻调度,即π(0)=0),可以得到:
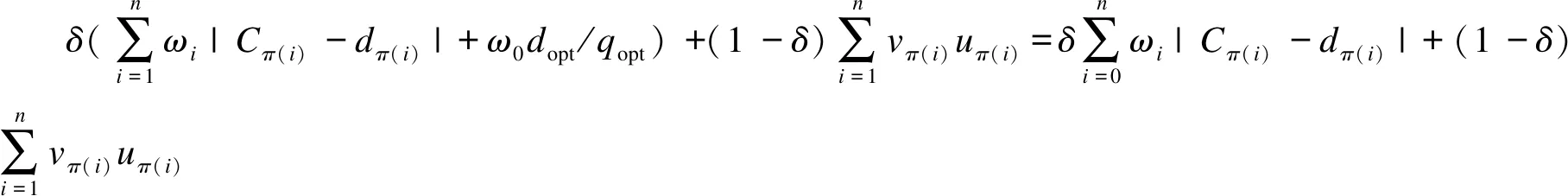

(4)
证明:与文献BRUCKER[20]的证明方法类似。

(5)
证明:与文献LIU等[21]的证明方法类似。


(6)
其中
Ω1=λ1+bλ2+b(1+b)λ3++b(1+b)n-2λn
Ω2=λ2+bλ3+b(1+b)λ4++b(1+b)n-3λn
Ωn-1=λn-1+bλn
Ωn=λn
(7)
对于共同工期(CON)指派方法,
(8)
对于松弛工期(SLK)指派方法,
(9)

=δ(λ1+bλ2+b(1+b)λ3++b(1+b)n-2λn)(pπ(1)-βπ(1)uπ(1))+
δ(λ2+bλ3+b(1+b)λ4++b(1+b)n-3λn)(pπ(2)-βπ(2)uπ(2))+
δ(λ3+bλ4+b(1+b)λ5++b(1+b)n-4λn)(pπ(3)-βπ(3)uπ(3))++
δ(λn-1+bλn)(pπ(n-1)-βπ(n-1)uπ(n-1))+
δλn(pπ(n)-βπ(n)uπ(n))+
其中Ω1=λ1+bλ2+b(1+b)λ3++b(1+b)n-2λn
Ω2=λ2+bλ3+b(1+b)λ4++b(1+b)n-3λn
Ωn-1=λn-1+bλn
Ωn=λn
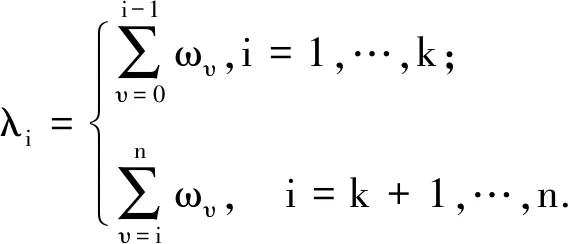
对于松弛工期(SLK)工期指派,证明方法相似。
从引理5,通过对式(6)中的uπ(i)(i=1,2,,n)求一阶导数,并令导数式子等于0,就可以求得最优uπ(i),由此得到如下引理。

(10)
其中Ωi(i=1,2,,n)是由式(7)给出。
设二进制变量Xir=1表示工件Ji排在位置r,否则Xir=0。从式(6)可知,最优排序(工件序列)能通过下面的线性指派问题得到。
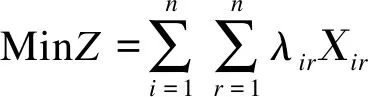
(11)
S.T.
(12)
(13)
Xir=0或1,i,r=1,2,,n
(14)
其中
(15)
Ωr由式(7)给出。
通过以上引理和分析,对问题

算法1
步骤1 对于CON共同工期指派问题,通过引理3计算k;对于SLK松弛工期指派问题,通过引理4计算l;
步骤2 通过式(11)~(15)解决线性指派问题,从而得到最优排序;
步骤3 通过引理6(式(10))计算最优资源分配;
步骤4 对共同工期CON指派方法,计算工期dopt=Cπ(k),对松弛工期SLK指派方法,计算qopt=Cπ(I)。
定理1算法1能在时间复杂度O(n3)内解决问题

证明根据引理1-6和线性指派问题,可得算法1的正确性。步骤2线性指派问题的复杂性为O(n3),步骤1,3,4的复杂性为O(n),因此算法1总的时间复杂性为O(n3)。
为了详细说明算法1的计算过程,我们举出如下的例子:
例1:本例仅考虑共同工期的情况(松弛工期情况计算步骤相似)。n=7,δ=0.5,b=0.05,位置权重分别是ω0=2,ω1=7,ω2=4,ω3=5,ω4=8,ω5=2,ω6=6,ω7=1,在表1中,给出了关于工件参数的其它数据。


表1 例子1的相关数据

表2 例1中λir的值(黑色字体为最优解)
3 结论

