基于双目视觉的无人机室内定位研究
2019-12-10郭关有姚仁和杜白雨赵志萍院老虎
郭关有,姚仁和,杜白雨,赵志萍,院老虎
(1.沈阳航空航天大学 航空宇航学院,沈阳 110136;2.上海航天技术研究院 上海宇航系统工程研究所,上海 201109)
随着技术更新和需求增长,无人机产业在军民两用方面得到了快速发展。对于无人机系统,能够准确定位的先进导航系统是实现其自主导航的基础。针对室内环境,多旋翼无人机因其明显优势成为大多数科研人员的研究对象。目前室内定位方式主要有基于测距仪的定位、基于声纳传感器的定位、基于视觉的定位、基于惯性导航和视觉融合系统的定位,以及其他多智能传感器的组合定位。但是这些方法尚未形成完善的体系,室内环境的复杂性、无人机状态的不确定性更是增加了自主定位的难度[1]。多种定位方式中,基于视觉的定位技术以其价格低廉、部署简单且不存在信号屏蔽等优点被研究人员关注[2-4]。
国外最早开展了有关基于视觉的无人机室内定位研究,从1966年开始,美国的麻省理工学院便开始了室内定位导航的研究[2]。AHRENS S.等人[5]开发了一种四旋翼无人机的系统结构和核心算法,通过视觉传感器,实现了无GPS室内环境下的无人机导航和避障。MUSTAFAH Y.M.[6]等人利用双目立体视觉传感器设计了一种无人机室内定位系统,实现了实时获取无人机的位置信息功能。最近,SANTOS M.C.P.等人[7]研发了一种低成本的定位系统,该系统利用RGB-D传感器、惯性测量单元(IMU)和超声传感器,基于光流算法实时估计无人机的速度数据。
在国内,何芳[8]设计了一套适用于无人机室内自主定位的半直接法视觉SLAM系统,能够高效地确定空间三维点的准确位置。陈晔[2]搭建了无人机双目视觉定位测试系统,以SIFT算法作为特征点提取与匹配的主要方法,实现了四旋翼的室内定位。张泽群[9]采用双目立体视觉,对四旋翼无人机在普通室内环境下的定位和避障进行了研究。最近,余莎莎等人[10]通过RSS(Received Signal Strength)定位算法进行了无人机自主三维定位研究,仿真实验表明,该方法具有精度高、无误差积累和适应性强的特点。
本文针对室内场景下的无人机定位问题,采用双目视觉传感器,利用简单地标和双目测距技术实现的RSS定位算法来实现无人机的室内自主三维定位。该方案的定位计算均由传感器采集的图像和完整的算法流程完成,因而具有定位自主性;相较于单目视觉定位系统,双目立体视觉系统定位精度更高,视角更广阔,通过采用RSS定位算法,避免了定位误差因航行距离增大而积累的问题;同时,该方案大大减少了图像数据和定位计算的处理时间,这对于实现无人机的实时定位非常重要。
1 理论分析
1.1 双目立体视觉测距模型
在计算机视觉研究中常用的坐标系有世界坐标系、相机坐标系、图像像素坐标系和图像物理坐标系。根据四个坐标系之间的转换关系和成像原理,可得到相机成像模型。
(1)
式中:Mi——摄像头的内部参数矩阵;
Me——摄像头的外部参数矩阵。
本文采用平行双目立体视觉系统,其简易模型如图1所示。该模型中两个摄像头的光轴彼此平行,成像平面共面,其优点是能最大程度保证测量数据的稳定[11]。

图1 平行式双目视觉测距模型
图1中,两个摄像头之间的距离定义为基线距B,焦距均为f,相机坐标系原点为左摄像头的光心点Ol(0,0,0)。假定左右摄像头在同一时刻对相机坐标系下的空间点P(XC,YC,ZC)进行拍照,分别在左右视图上得到投影点的图像像素坐标为pl=(ul,vl)和pr=(ur,vr),经过立体校正后两个光心原点将处于同一水平高度,即vl=vr。根据摄像机的投影几何关系可以得到式(2)。
(2)
定义视差d=u1-ur,联立式(2)中两项并代入vl=vr,可以得到式(3)。
(3)
在已知摄像头内参矩阵和匹配特征点视差的前提下,空间点在相机坐标下的三维坐标可由式(3)唯一确定。于是,双目同步摄像头模组基线的中点M(即质心)距离空间点P的相对距离为
(4)
1.2 无人机室内自主定位算法
本文基于RSS定位算法,通过设计地标进行辅助定位来求解预设世界坐标系中无人机的三维坐标。
(1)地标设计
根据地标设计的一般要求[12-13],以及本文利用地标实现辅助定位的需求,设计地标如图2所示。此地标的设计形状非常简单,具有易于视觉算法识别的主体部分(除字母区域之外的部分,实物设计为红色),且地标之间可利用特征明显的字母做区分(实物设计为黄色),适宜于在室内环境下进行识别定位。

图2 地标设计(字母为A、B、C、D的情况)
此地标的设计能够使其与周围的地面环境区别开来,易于图像处理算法对其识别,能在一定程度上克服室内光线不足的问题;矩形当中的字母可作为SURF算法的特征点提取部分,能够很好地简化特征点提取算法,提高算法的运算速度和特征点匹配的准确性。
(2)无人机定位算法
将平行双目摄像头安装在无人机的底部,左右摄像头光轴互相平行且关于无人机机轴对称,并使其相对无人机的位置固定。当无人机在室内飞行时,应保证三个地标都能被双目摄像头拍到(地标呈三角形状布置),如图3所示。
图3中D1、D2、D3分别为点M到三个地标形心点的距离,由式(4)求解得到。为研究方便,假定:1预设世界坐标系中三个地标的形心坐标分别为P1(XW1,YW1,ZW1)、P2(XW2,YW2,ZW2)和P3(XW3,YW3,ZW3),为已知量;2当无人在室内上空飞行时,可以抽象为其质心CM的运动,其机载双目同步摄像头基线中点M的三维位置就可以近似为无人机当前的位置,记为M(XW,YW,ZW),为未知量。
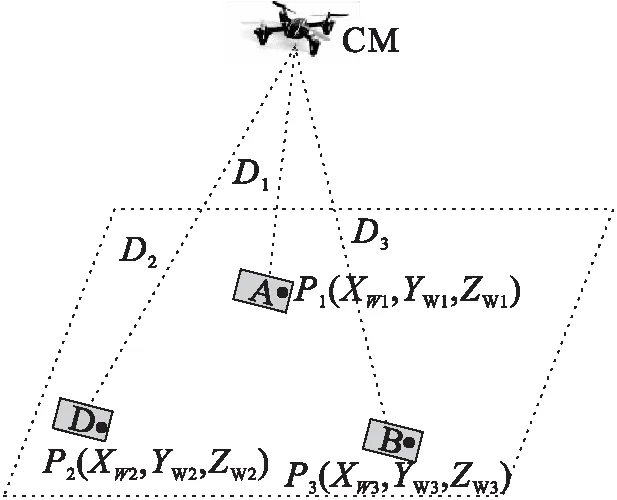
图3 无人机定位几何关系
根据无人机定位的几何关系,有:
(5)
式(5)中,由于地标处于同一平行地面,因此令ZW1=ZW2=ZW3=0,将式(5)整理成未知量为XW、YW矩阵方程:
AX=B
(6)

式(6)为二元非齐次线性方程组,根据最小二乘法原理,可求得未知量横纵坐标X为
(7)
将式(7)代入式(5)中第一个等式可以求出纵坐标为
(8)
至此,可以得到基于双目视觉测距算法的无人机位置坐标估计值M(XW,YW,ZW)。
1.3 双目摄像头模组的标定
通过考虑摄像头畸变的径向分量和切向分量,基于经典的张氏标定法[14]对双目摄像头进行标定。
本文采用的双目同步摄像头模组型号为树莓派HBV-1714-2 S1.0。利用其提供的USB接口,选择模组分辨率为1 280×480,基于MATLAB GUI开发了图像采集系统。设计8×11的黑白棋盘格标定板,每个方格的边长均为50 mm。
基于图像采集系统和棋盘格标定板,利用MATLAB立体相机标定APP对采集到的16对棋盘格图像进行标定。通过修正标定参数的重投影误差,最终使其全部小于0.14,得到双目同步摄像头模组的标定参数见表1至表3所示。由于模组两个摄像头焦距不变,相对位姿也已固定,因此这些标定参数可作为已知量直接用于后面的计算。
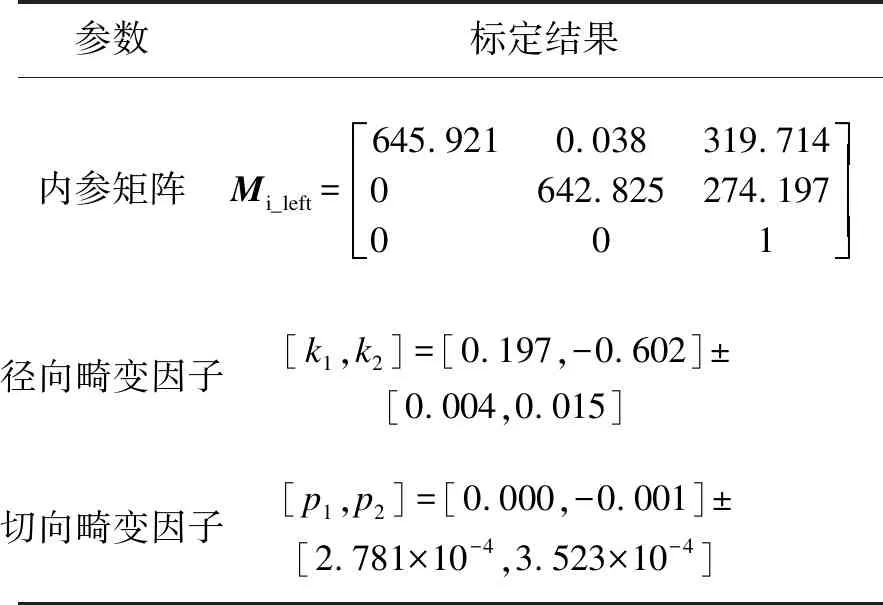
表1 左摄像头主要参数标定结果
2 地标识别与定位
2.1 地标的识别与分割
在室内环境下,本文设计的地标(实物需要彩色打印)对于图像的分割是一个很有用的线索,可以通过对所拍摄图像进行颜色的K-means聚类分析实现对地标的识别,这样可以有效地避免光线不足对图像分割造成的干扰。

表2 右摄像头主要参数标定结果

表3 双目摄像头模组的相对位姿标定结果

图4 地标识别算法流程
地标识别过程的程序步骤如图4所示。采用K-means聚类分析图像分割算法,将彩色图像(包含地标)每个像素的RGB值作为样本数据集X进行划分,再根据对含地标图像的预先认知,指定图样的点集(聚类数目)数量K。基于K均值的颜色分类将会把样本数X转换成xy色度坐标,然后使用K-means算法找出xy色度平面上的聚类点集,Peter Corke对此方法做了研究[15]。根据对图像的预先认知,地标区域的像素数目应远小于非地标区域的像素数目,因此可通过比较两个点集中像素的数目之和的大小来进行判别,较小者的即为地标区域所对应的点集。在实际拍摄的图像中,字母所占区域很小,因此只考虑主体区域和字母区域进行颜色分类,指定图像的聚类中心数量为K=2对地标进行识别。
基于上述算法,对一幅480×640×3实例图像进行地标识别试验,图中地标的尺寸为(9×13)cm,样本数据集X=480×640。算法可将地标区域成功地从图像中分离,将其显示为地标二值图像,可看到图像中存在毛刺、小点和小裂缝等噪声,如图5所示。

图5 地标识别结果及缺陷标记
图5所示的地标二值图像具有明显的矩形特征,基于形态学的形状滤波器可利用形态学算子有效地滤除噪声,保留图中原有信息[16]。本文利用二值形态分析方法中的基本运算,即腐蚀、膨胀以及由它们组合得到的开闭运算实现图像的去噪。根据图像开运算和闭运算特点,对图5先执行闭操作,再执行开操作,得到结果如图6所示。对比发现,图像中的噪声点已经消失,得到了完整的矩形地标。
本文采用基于统计二值图像不规则连通区域的八连通方法,通过检查图像中每个像素与相邻像素的连通性,使用MATLAB分别求取每个地标的形心坐标和最小外接矩形,结果如图7所示。

图6 地标二值图像去噪

图7 地标形心和最小外接矩形计算结果
可以看出地标的形心和最小外接矩形能被很好地识别出来,并得到了三个地标在图像像素坐标系下的形心坐标和最小外接矩形坐标范围。
2.2 地标形心定位计算与误差分析
根据模组参数标定结果,模组基线的实际距离为B=11.999 cm,将其和表1、表2的相应数值和地标形心坐标代入式(3)计算得到相机坐标系下的坐标估计值(XC,YC,ZC),与真实值进行比较如表4所示。

表4 地标形心坐标真实值与估计值(单位:cm)
通过计算绝对误差,发现相机坐标系下地标形心坐标XC和YC的实际值与估计值之间的最大误差为3.26 cm,其余误差都在3 cm以内,基本上能够满足定位精度需求。但是坐标ZC值的误差过大,都在6 cm以上,属于不可接受的范围,因此后面将利用SURF算法进行更精确垂直距离的测量。
2.3 基于SURF算法的垂直距离测量
SURF算法又称为加速鲁棒性特征,许多研究的实验证明其运算速度要比SIFT算法快很多,综合性能优异,被广泛应用于计算机视觉、导弹制导时的目标识别和机器人导航等领域[17-18]。
(1)基于立体校正和地标区域匹配约束的SURF立体匹配
本文针对其匹配误差和计算速度问题,先基于Bouquet校正原理对图像进行立体校正预处理,并通过地标最小外接矩形确定的地标范围添加特征点匹配约束。针对某一图像对的立体匹配步骤如下。
①读取RGB格式的图像对,分别进行图像中地标的识别、分割和最小外接矩形的计算;
②根据地标最小外接矩形数据,确定地标区域图像像素坐标值的范围,将其作为地标区域的判断条件;
③读取原始图像,进行立体图像校正、SURF特征点检索和描述算子生成;
④计算所有匹配点的最小距离,按匹配距离误差从小到大生成特征点匹配向量;
⑤指定需要的特征点个数,按匹配距离误差从小到大读取。每读取一对特征点,就判断其像素坐标值是否在第二步所设定的地标区域内,若是,则作为最佳匹配输出;否则,将其从最佳匹配中剔除。
基于上述算法步骤,指定目标特征点匹配对数为30,对2.1节中的图像对进行立体匹配计算,结果如图8所示。可以看出,所有特征点匹配对全部落在地标区域内,无误匹配现象。
将对SURF立体匹配算法改进前后的相关数据比较如表5所示(准确率:落在地标区域内匹配对数和总匹配对数之间的比值)。对比发现,基于立体校正和地标区域匹配约束的SURF立体匹配已经很好地达到了目标。

图8 基于改进SURF算法的图像立体匹配

参数未校正校正校正+区域约束误匹配对数310准确率83.3%90%100%
(2)基于多幅图像的垂直距离计算及数据拟合
为了确定双目摄像头模组能够准确测量的距离范围,以及获得更精确的垂直距离,采集不同距离的多幅实验图像进行视差和垂直距离计算,并拟合真实距离与图像视差数据。通过比较拟合多项式模型计算结果和式(3)第三项计算结果,选出误差较小的作为本文的垂直距离计算模型。
本次试验共利用三个地标(A、B、D),将其平行于地面布置。假定无人机在室内的飞行高度在(1~3)m之间,结合模组的有效测量距离,设计三个地标的尺寸均为(18×13)cm,它们的相对距离如图9所示,三个地标的形心构成一个等腰三角形。
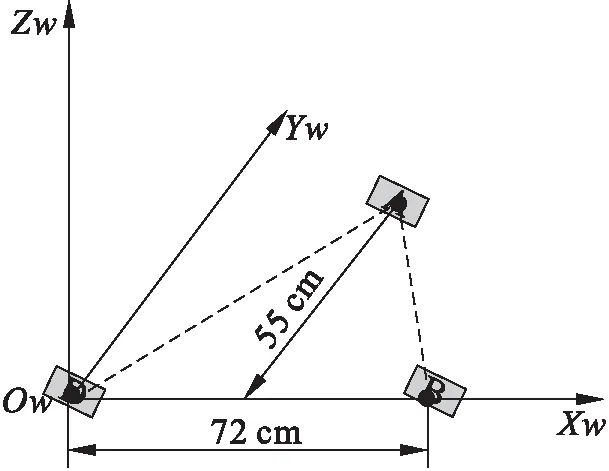
图9 预设世界坐标系及地标布置
根据模组的有效测量距离,从104 cm处开始采集图像,采集的高度范围为104~204 cm(增幅为10 cm,利用精准测距仪测得)。利用基于立体校正和地标区域匹配约束的SURF立体匹配方法进行匹配计算,指定最佳匹配对数为30,得到只属于地标区域的最佳匹配特征点并计算其视差,按照匹配距离误差从小到大的原则取前4组视差数据,将其平均值作为该地标形心的视差数据。对所有11组图像进行视差计算,结果代入式(8)得到垂直距离ZC估计值如式(9)所示。
(9)
计算真实值和估计值的绝对误差,如图10所示。可以看出,大部分误差都在3 cm以内,随着测量距离的增加,绝对误差有增大趋势。考虑到超过200 cm以后,误差会进一步增大,因此去掉200 cm以后部分的视差数据,确定本文采用模组在当前地标布置情况下的有效测量距离为1~2 m。

图10 垂直距离估计值绝对误差随距离的变化
根据式(9)所示的测距模型,垂直距离ZC和视差d之间为反比例关系,Bα为标定常数。利用经验公式,可引入误差距离e改进垂直测距模型如式(10)所示。
(10)
将真实垂直距离ZC作为因变量,视差的倒数1/d作为自变量,通过多项式拟合来求解未知常数。用MATLAB分别对三个地标的数据进行多项式拟合,通过比较均方根误差(RMSE),选择一次多项式拟合,分别得到地标A、B和D垂直距离拟合表达式如式(11)~(13)所示。
(11)
(12)
(13)
基于这些拟合函数和视差数据计算得到拟合函数模型距离估计值ZCF,计算其与真实值之间的平均相对误差ARE_CF,与未引入误差限e得到的距离估计值ZC的平均相对误差ARE_C进行比较,如表6所示。

表6 两种距离估计方式相对误差均值比较
可明显看出,通过拟合一次多项式模型求解得到的距离估计值的平均相对误差普遍较低,故本文将利用拟合多项式模型计算垂直距离。至此,通过图像处理已经可以得到相机坐标下地标的三维坐标(XC,YC,ZC)。利用式(4)至式(8)就可求解得到无人机的三维坐标(XW,YW,ZW)。
3 室内定位仿真实验
本文采用的是平行双目摄像头模组立体视觉定位系统,根据对无人机定位算法的假定条件,可将双目同步摄像头基线中点的三维位置近似为无人机当前的位置。因此,可用双目摄像头模组模拟无人机飞行,并拍摄一系列图像数据。
实验仿真平台的硬件包括树莓派HBV-1714-2 S1.0双目摄像头模组(模拟无人机)、USB图像传输线,以及图像数据处理平台战神K650D-i7 D3笔记本电脑(配置为CPU核处理器i7-4710MQ,内存8G)。根据前面的图像处理和无人机定位算法得出无人机整体定位流程框图如图11所示。基于无人机定位流程结构框图和MATLAB GUI设计应用程序如图12所示。

图11 基于双目视觉的无人机室内定位流程框图

图12 无人机定位仿真系统软件界面设计
采用和图9一样的世界坐标系和地标布置,可得到地标在预设世界坐标系中的坐标。让双目摄像头模组模拟无人机在室内地面上空(1~2)m的范围内沿一条不规则路径飞行,拍摄得到23组图像对序列,并利用精准测距仪测量得到了真实轨迹点的坐标。利用定位仿真系统,计算得到无人机室内仿真轨迹如图13所示。
三个坐标值仿真结果的绝对误差如图14所示,可直观看出误差在可接受范围之内。
均方根误差(RMSE)对一组数据中的最大和最小误差反映非常敏感,可以很好地反映出室内定位的精度。本文将其作为定位误差大小地评价标准,如式(14)所示。

图13 真实轨迹和仿真轨迹比较(单位:cm)

图14 仿真结果的绝对误差
(14)
式中,n为测量数据个数,Xobs,i为真实值,Xmodel,i为模型测量值。利用此公式分别计算三个坐标值的均方根误差,结果如表7所示。

表7 定位均方根误差 cm
可以看出,三个坐标值的定位精度都在3 cm以内。此定位精度基本满足预定要求,说明在室内飞行高度为1~2 m且拍摄图像中包含地标的范围内,本文的定位方案能够实现比较精确的无人机室内定位。
4 结论
本文提出了一种基于K均值图像分割、SURF立体匹配和RSS定位算法的无人机室内定位流程。仿真实验表明,该流程在一定的空间范围内能有效实现无人机的定位,且定位精度较高。通过设计简单的辅助定位地标,充分利用了K均值和SURF算法的优势,对图像的地标区域进行处理,最终得到了目标特征点,可以较快的速度计算出无人机位置。此定位方案具有精度高、成本低、计算速度快和不受电磁干扰等特点,但是定位范围十分有限,可通过布置三个以上地标实现更广范围的室内定位,存在一定的局限性,还需要进一步改进。
