无人艇防空机动模型及仿真分析

杨罗章,胡生亮，罗亚松

(海军工程大学兵器工程学院,湖北 武汉 430033)

水面无人艇具有体积小，环境适应性强，隐蔽性好，机动灵活，无人员伤亡等优点,成为现代无人作战系统中一个重要分支。其使命任务也不仅局限于巡逻警戒、监视侦查等任务,在水面无人艇上搭载武器系统,配合大型舰艇执行反舰、防空反导、反潜、对岸火力支援等硬杀伤任务,拓展丰富海上作战样式,也成为其重要发展趋势[1-3]。其中,无人艇搭载防空导弹前出水面舰艇拦截反舰导弹,增加水面舰艇的有效反导远界,是提高大型舰艇抗饱和攻击能力、提高拦截和抗击反舰导弹成功概率的有效方式。与有人舰艇执行防空反导任务相比,无人艇防空反导应最大限度减少人在回路的控制,一方面可以提高其执行作战任务的实效性,另一方面可以满足其智能化和自动化的控制要求。因此,根据无人艇典型结构和防空反导需求构建机动模型,使其全自动执行作战流程是无人艇防空反导的一项重要研究内容。本文以搭载防空导弹的水面无人艇为研究对象,以无人艇执行防空反导任务时拦截概率最大化为目标,对无人艇防空机动进行研究。

1 无人艇机动

无人艇机动,即无人艇为达成战术目的,相对于目标所进行的变换位置或保持位置的运动,目的是抢占和保持有利阵位,充分发挥己方武器的威力,阻碍敌方武器的使用或降低其效果。无人艇的机动样式,主要包括定向定速机动、定舷角运动、混合机动和曲折机动[4-5]。

1)定向定速机动,亦称直航向机动,机动过程中航向航速不变,是最基本的机动样式。双方定向定速机动时,要采取最佳的航向、航速和相应的机动时间,以使阵位要素的变化对己方有利。

2)定舷角机动,是在机动过程中或一段时间内,保持本艇舷角不变的机动。

3)混合机动,是一方做定向定速机动,另一方做定舷角机动。

4)曲折机动,亦称“之”字运动,是采取有规律或按预定方案无规律变向(有时也变速)的机动,对于阻碍、规避敌方使用炸弹的攻击和降低敌方舰炮射击效果有良好作用。

无人艇防空作战时,由于无人艇速度相对于空中来袭导弹目标的速度很慢,基本可以忽略不计,因此,无人艇的防空运动可看作是混合机动,即无人艇做转向机动,目标做定向定速运动或曲线运动。

2 无人艇防空导弹跟踪区及射界分析

无人艇上使用旋转发射架的防空导弹,安装在艇艏时,其物理模型如图1所示。假设无人艇防空导弹的最大射程为R,高度值为h的点M为导弹最远射击距离上一点。以无人艇为原点,建立如图2坐标系,Y轴为无人艇的初始航向Cw方向,X轴在水平面内垂直于Y轴,指向无人艇右舷,H轴垂直水平面向上。

图1 无人艇物理模型图

图2 无人艇防空导弹跟踪区及射界坐标系

无人艇的结构特点制约着其防空导弹的可跟踪俯仰角和舷角,从而使防空导弹存在部分跟踪死区[6]。防空导弹的最小可跟踪俯仰角与可跟踪舷角关系如图3所示。

图3 最小可跟踪俯仰角与可跟踪舷角关系图

在导弹发射时,为保证无人艇自身的安全,取发射安全角为ΔQ,为满足防空导弹的导引头对目标捕获跟踪,又满足导弹的可发射舷角[7-8],则无人艇的最小发射舷角Qmin、最大发射舷角Qmax、最大水平射距r与目标高度h的关系为

(1)

3 无人艇防空作战机动模型

3.1 无人艇机动最优解分析

若无人艇位于点O,航向为Cw=0;目标位于T点,方位为Cm,斜距为Rm,高度为h,目标相对于无人艇的速度为Vm,敌舷角Q=Cm-Cw,假设目标做匀速直线运动,通过目标与目标相对速度方向一致的射线为目标航路。以无人艇为原点,建立如图4所示水平坐标系,Y轴为无人艇的初始航向Cw方向,X轴在水平面内垂直于Y轴,指向无人艇右舷。

图4 坐标系示意图

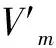
(2)

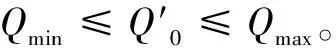
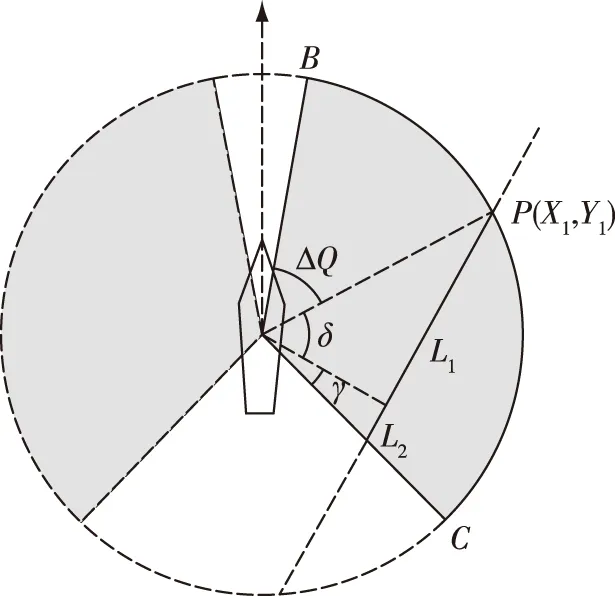
图5 可靠射击区示意图

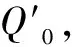
当目标航路捷径d>0时,由于d和导弹的最远水平射距r是已知的,则

(3)

因此,角度δ和距离L1的值变为已知,由于L=L1+L2,则当L2值取最大时,L也得到最大值。而L2=d×tanγ,因此,求解L的最大长度问题可转化为求解角度γ的最大值问题,而

γ=Q2-Q1-δ-dQ,dQ≥0

(4)

图6 无人艇机动目标示意图

3.2 无人艇机动方案

无人艇的机动方案为:转向机动,保持对目标的射击点P的舷角在导弹射界范围内,且可靠射击区长度最大。定义转向角ψ以无人艇航向为基准,顺时针方向为正,即ψ>0时,无人艇向右转向;ψ<0时,无人艇向左转向,其取值范围为[-π,π]。

ψ的值确定与两个条件有关:一是射击点P的舷角大小;二是无人艇相对于目标的方位φ。

ψ的值分为以下几种情况:

1)φ=0时,即目标航路捷径d=0时,转向角ψ为

(5)

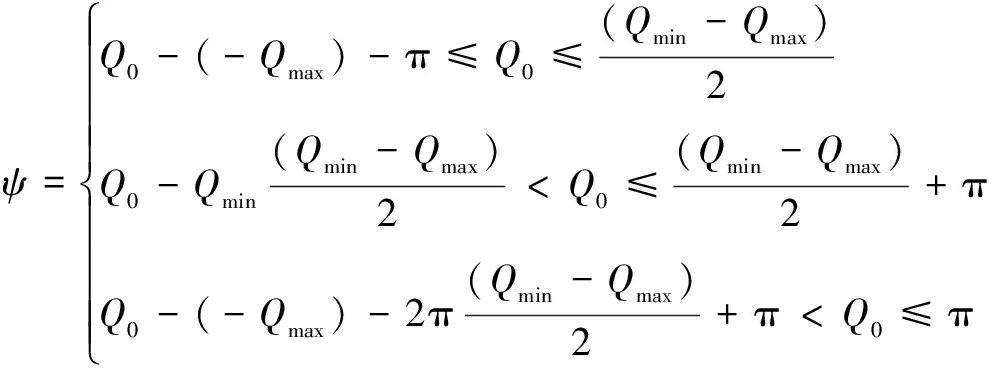
(6)

(7)

4 机动模型仿真验证

假设无人艇初始航向Cw=0,以无人艇为原点O建立水平坐标系,Y轴方向为无人艇初始航向,即正北方向;X轴在水平面内垂直于Y轴,指向无人艇右舷。

T=0时刻,发现敌目标位于点Μ(20 km,15 km,0.5 km),水平相对速度Vm=50 m/s,初速相对速度方向α=-135°(以正北,即Y轴为基准,顺时针为正,逆时针为负)。

假设防空导弹的最远射击斜距R=4 km,无人艇的平均转向角速度ω=0.05 rad/s,艇艏部分形成遮挡的最大仰角θ1=15°,水平舷角Q1=15°,上层建筑遮挡的最大仰角θ2=60°,水平舷角Q2=145°。取最低发射俯仰角θ0=0°,发射安全角ΔQ=10°,由目标高度h=0.5 km,根据式(1)可得无人艇防空导弹的射界范围为

(8)

假设目标做匀速曲线运动,目标航向以0.005 rad/s的修正速率向无人艇机动,则其运动方程为

(9)

目标运动轨迹仿真如图7所示。

可由式(2)得T时刻防空导弹射击点P的坐标(Xp,Yp)为

(10)

则射击点P的方位角Qp为

(11)

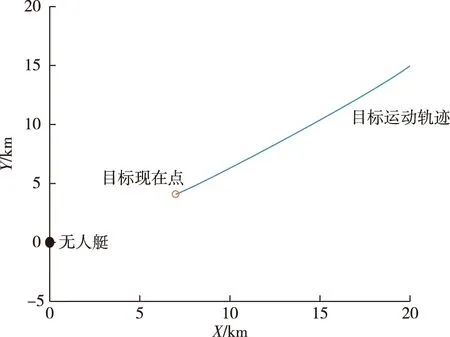
图7 目标运动轨迹图

则目标方位,射击点P的方位及无人艇航向随时间变化关系如图8所示,由图8可知:

图8 各角度变化曲线

1)无人艇初始航向为0,做曲线运动;

2)在A点之前,目标处于防空导弹射界之外,求解的射击点P(即目标航路延长线与导弹射距的交点)的方位逐渐减小;

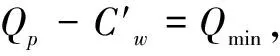
4)A点以后,无人艇转向机动始终保持射击点P相对于无人艇舷角不变,即在曲线中间段,保持射击点P的方位与无人艇航向之差恒定,为最佳射击舷角Qmin;

5)目标进入导弹的射界后,即对应B点以后,导弹以目标现在点为射击点。此时,导弹具备发射条件。

5 结束语

水面无人艇搭载防空导弹执行防空反导任务时,通过无人艇防空导弹跟踪区及射界计算,可明确无人艇机动的约束条件。以拦截导弹概率最大化目标,可求解出不同航路捷径条件下无人艇机动的最优解。针对不同战场态势,即可确定无人艇机动方案。仿真结果表明,所提出的无人艇防空机动模型及机动方案合理有效,为水面无人艇执行防空反导任务实际运用提供了有价值的参考。