浅谈初中几何教学中学生思维的激发

罗华金

初中数学几何教学一直是初中数学老师们重视的教学内容之一，因为几何问题的证明过程中最能体现数学思维能力和逻辑推理能力，过中乐趣真叫做趣乐无穷，故人们常说：“数学是思维的体操”真是名副其实，作为一名初中数学教师的我是怎样在自己的教学中激发学生的思维能力的呢？

首先重视基本几何概念、定义、定理、性质、推论、公理等基础知识的教学，很多几何图形都源于我们的实际生活，密切联系我们的实际生活相关的几何图形，把它们规范到数学上来如何准确定义，让学生感受到原来如此熟悉，并不陌生，增加了学习的兴趣，降低了理解的难度，例如两点之间的的距离是指：连接两点之间线段的长度，为了帮助同学们理解清楚这一概念，我列举出生活中的实际例子：比如班上甲同学与乙同学现在所处的位置有多少种到达方式？学生的思路一下就打开了……，指出了很多种到达方式;再次我在黑板上任意画了两个点，又问到：有多少种连接方式？请学生上黑板来画，学生的思路很轻松被激发，画了很多种弯弯曲曲的线把两个点连结起来了;那么所有的这些连线中那一条线的长度才是这两点之间的距离呢？是连接两点之间的线段还是这条线段的长度？请同学们展开思考后并讨论，最后的结论是：两点之间的距离是指连接两点之间线段的长度，从而进一步理解两点之间线段最短也就迎刃而解了，当然有了这一距离的理解基础，在以后的学习中，同学们自然就很容易理解点到直线的距离以及两平行线间的距离了。

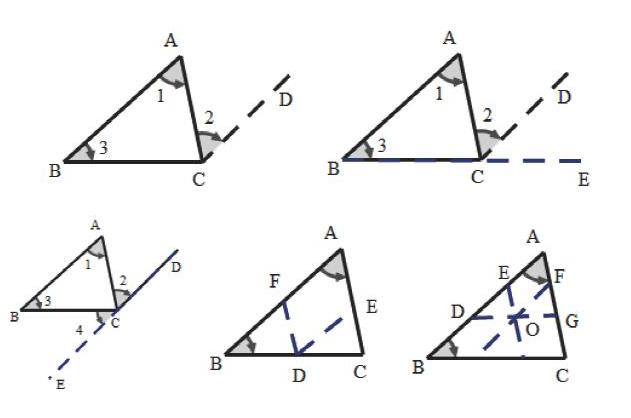
又比如说三角形的内角和为 定理的证明的教学，我请同学们课前准备了一张三角形的纸片（形状不限），并思考如何验证三角形的内角和为 ，在课堂上，同学们争先恐后地上来一一展示了他们的思路，同学们展示一种思路，我就把他们的思路的图形画下来，主要有如下几种方式：

然后，我再启发同学们一一加以推理证明，并选出最优方案，大大激励了同学们学习几何的兴趣和乐趣，看到同学们脸上露出的喜悦我倍感欣慰。

其次重视学生分析问题能力的培养和训练，几何证明题的思路如何寻找？这是困惑很多同学的难点所在，许多同学对数学的畏难情绪就产生在这里，如何帮助同学们度过这一难关呢？我在教学中是这样做的：第一：培养同学们读题的能力，具体做法是：1.读一个已知条件分析一个已知条件（结合图形分析它能产生什么结论）;2.结合每个条件之间还可产生些什么样的结论;3.每个条件产生的结论之间又可产生什么结论？4.分析求证，逆向思考：要证明此结论需满足什么条件？倒过来寻求与已知条件之间的桥梁和纽带在哪里？这个过程中的教学中我会耐心细致地引导学生跟着我的思路细心体会，慢慢学着我的思维方式进行实战演习和训练，此时教师需要的是一份耐心、等待和鼓励我们的学生，慢慢来……

比如我在讲解题目：如图，四边形ABCD中，对角线相较于点O，E，F，G，H分别是边AD，BD，BC，AC的中點，求证：四边形EFGH是平行四边形时，仍然引导同学不急不躁地认真读题，一一分析好每个已知条件：①四边形ABCD能产生什么结论？学生回答道：四个内角和为360度，还可转化成三角形解决问题，教师积极鼓励同学们：好一个转化成三角形来解决问题的思路，点赞！;②点E，F，G，H分别是边AD，BD，BC，AC的中点又想到了什么呢？一个同学回答到：在三角形ABD中，EF是它的中位线，所以 同理在三角形ABC中，GH是它的中位线，所以  EF=GH，    ，很精彩的分析，迎来了同学们热烈的掌声，读完已知条件，分析完已知条件就把问题证明完了，漂亮，在次点赞！我进一步启发到：还有别的方法证明四边形EFGH是平行四边形吗？同学们很轻松回答到：只需证明 和 就可以了;紧接着另一个同学迫不及待回答到：还可以证明 ，精彩，我为你们鼓掌。

学习数学，就是学习数学思维方式，只要我们重视学生的思维方式的培养，即：教会同学们如何分析已知条件以后，一些简单的题目只需分析完已知条件就可清晰地找到解题思路;重视如何分析求证（结论），一些题目需要结合已知条件产生的结论和求证需要什么条件，二者相结合便会很快找到思路;但是有些题目当二者相结合都找不到解决方法时，则需要合理的添加辅助线来解决，这便是同学们感觉最难的问题了，但是，只要我们老师不急不躁，教会同学们一些基本的添加辅助线的方法之后：知道什么条件便可想到添加什么辅助线，就好像打拳一样，一招一式都是有套路，有招数的就不可怕了。

再次，重视学生分析能力的培养，这是学生几何分析能力提升的核心和关键所在，我们许多老师喜欢我陶醉，一讲到底，总害怕学生不会，总放心不下学生讲不好题，总担心学生讲题会耽误自己的教学进度，其实这些担心和放心不下都是多余的，也是错误的，所以为了最大限度激发学生学习数学尤其是学习几何的学习积极性和兴趣，我的体会和做法是这样的：放心、放手让学生讲题。

最终目的：让学生随意拿到一个题都能分析，都能具备找到解决问题的能力和方法，而且能创造性的解决问题，超越我们老师的思路和方法，那是何等的愉快！数学几何证明题的分析能力的培养，思维能力的提高核心在于充分相信学生有无限的潜能，我们老师要做的只是竭尽所能不遗余力去挖掘学生的潜能，给学生搭建一个展自己才能的舞台，让学生有展示自己的机会，增强学生学习数学的积极性和兴趣莫过于在此吧！