基于尖点突变理论的软岩弃渣路堤局部稳定性分析

2019-12-09鞠兴华杨晓华张莎莎

水文地质工程地质 2019年6期

鞠兴华，杨晓华，张莎莎

(1.潍坊学院建筑工程学院，山东潍坊 261041;2.长安大学公路学院，陕西西安 710064)

软岩在我国分布广泛。随着经济的快速发展，软岩地区的公路建设日益增加，但其“似土非土、似石非石”的特性也带来诸多工程问题。目前，软岩弃渣在路基填筑中的合理性问题已被广泛关注[1-2]。鉴于软岩具有水理性差、强度低、成分复杂等特征，许多学者对其在路基填筑中的可行性和适用性进行了深入研究。张静波等[3]利用动三轴试验分析了软岩填料在干湿循环条件下的动力特性，为工程施工提供了的参考依据；毛雪松等[4]探讨分析了不同颗粒级配及水泥掺入量对路基填料CBR值的影响，确定了两者的最佳组合；宋杨等[5]对路基压实度的影响因素进行了研究，得出了施工参数与压实度间的影响关系，合理指导了实际施工；毛雪松等[6-7]对以千枚岩作为路基填料的施工工艺进行了设计，并根据现场实测结果进行了技术改良；赵德新[8]、詹永祥等[9]在填筑材料性能研究的基础上，探讨了不同填筑参数的组合施工效果，并提出了相应的控制措施，为类似软岩路基的填筑施工积累了经验。上述研究取得了一定的成果，但多偏重于路基填料的工程性质分析，未涉及路基填筑后的稳定性评价，也未涉及尖点突变理论的应用；同时，不同地区的软岩性质具有差异，加之地质环境条件不尽相同，因此需对不同地区的软岩路基填筑进行针对性的研究。

成武高速(成县—武都)共设计30余座隧道，岩性以红层软岩为主，伴随隧道开挖，将会产生大量软岩弃渣。由于工程地处长江上游环境保护区，工程区的水土保持、生态保护具有严格要求，其弃渣存放面临多种问题，如耕地占用、破坏地貌景观等；且成武高速地处陇南山岭重丘区，交通较为不便，使得路基填料取土困难，严重影响工程的经济效益。因此，若能将隧道弃渣用于路基填筑，将会大大降低投资成本，具有很好的实用价值。综合上述，本文以成武高速公路为工程实例背景，分析了路基填筑材料的工程特性；结合路基沉降监测数据，分析路基填筑后的稳定性及其发展趋势。

1 工程概况

成武高速公路是甘肃省境内的重点建设项目之一，具有特殊的作用和地位。该高速公路主要涉及9个乡镇，起点位于陇南市成县，终点位于武都区城郊乡，设计行车速度80 km/h，路基宽24.5 m，全长为92.04 km，其中包含4.4 km的二级公路连接线[10-12]。

如前所述，成武高速公路包含30余座隧道，岩性以泥质粉砂岩和粉砂质泥岩为主，红色，属红层软岩，具不等互层结构，亲水性强、透水性弱、强度低(一般小于30 MPa)、软化性强，且失水后易崩解；同时，岩层层面遇水易滑动，岩体层面之间抗剪强度低，特别是层面之间含水后易产生层间滑动。

2 工程特性分析

2.1 筛分试验结果

根据隧道开挖过程，区内弃渣具有明显的差异性特征，主要体现在颗粒成分、颜色及粒径等方面。为综合、全面分析区内弃渣的工程特征，该文以颗粒成分、颜色及粒径等为划分指标，将弃渣划分为三类(Ⅰ类、Ⅱ类、Ⅲ类)，并对三类弃渣进行试验分析。其中，筛分试验结果表明，Ⅰ类弃渣属巨粒混合土，红褐色，巨粒土含量为15%～50%，不均匀系数为12～30，曲率系数为0.82～4，波动性较大，但平均结果的级配较好；Ⅱ类弃渣属砾类土，红色，砾类土质量占比大于总质量的50%，不均匀系数5～8，曲率系数0.5～0.8，波动性相对较小，级配较好；Ⅲ类弃渣属巨粒土，灰色，巨粒组含量间于50%～75%，不均匀系数6～10，曲率系数0.5～1.28，级配较好。对比三类弃渣的筛分结果，得出不同弃渣的级配虽具有一定的差异，但整体级配分布区间一致，均属级配较好，基本符合路基填筑要求。

2.2 击实试验结果

由于成武高速泥质软岩弃渣中的大尺寸颗粒相对较多，有些粒径已经超过规范规定的标准重型击实试验的试桶要求，为了使试验结果更加可靠，研制了适用于大颗粒的大型击实试验。其中，标准重型击实试验的锤底直径5 cm，锤质量4.5 kg，落高45 cm，试样高度12 cm，试样体积2 177 cm3；大型击实试验击锤直径5 cm，击实锤重量4.5 kg，击锤下落高度45 cm，所用试模尺寸直径30 cm，高度35.4 cm，体积25 000 cm3。结合前述级配分析结果，Ⅰ类和Ⅲ类弃渣采用大型击实试验，Ⅱ类弃渣采用标准击实试验，三类弃渣的击实试验结果如表1所示。可以看出Ⅰ类弃渣的最优含水率最高，Ⅲ类弃渣的最大干密度最大，且三者的平均最优含水率为6.5%，平均最大干密度为2.27 g/cm3。同时，结合现场钻孔取样后的岩石试样数据，两类原岩的天然密度为2.42～2.55 g/cm3，少量可达2.6 g/cm3，而含水率则为3.0%～4.5%。与室内击实试验成果对比可知，路基填筑后的最佳密度要适当小于原岩状态的密度，这与开挖后的松散及填筑工艺相关。

表1 击实试验结果

2.3 CBR试验结果

在前述击实试验的基础上，按照最优含水率制备CBR试验试样。在CBR试验过程中，需进行浸水膨胀，该过程为：在试件面部铺设薄滤纸，并将其放置于多孔板上，用拉杆固定试样筒和多孔板；对试样筒进行倒转，在其另一面也放设滤纸，并在该面上放置多孔顶板及4块荷载板，每块荷载板1.25 kg；将整个装置放入水槽中，并安装好测定膨胀量的装置，在初始读数读取后，向水槽内注水，水面应高出试件25 mm，浸泡时间为96 h；量测浸水后试件的高度，计算膨胀量；卸除膨胀量测定装置，取出试样筒，吸去试件顶面的水，静置15 min后卸下荷载块、多孔顶板和多孔底板、滤纸，称试样筒和试件总质量，计算试样含水率和干密度的变化。最后，采用微机控制电子式万能试验机进行贯入试验。

在试验过程中，对贯入深度2.5 mm和5 mm均进行试验。根据试验及统计，得到CBR试验结果(表2)。

表2 CBR试验成果

在不同贯入深度条件下，均以Ⅲ类弃渣的CBR值相对更大，说明Ⅲ类弃渣的路基填筑性质相对更佳；同时，在各组试验中，对比贯入深度为2.5 mm和5 mm时的CBR值，得出前者均小于后者，因此，以贯入深度为5 mm时的试验结果为采用值，且三类土的CBR5.0值均满足高速公路填筑路堤的强度要求。

综合上述对弃渣工程特性的分析，得出成武高速的软岩弃渣具有较好的工程特性，可作为路基填料，但是在路基填筑过程中，应严格控制含水率，建议将含水率控制在6.5%左右。

3 稳定性现状评价

3.1 基本变形特征

在完成路基填筑以后，为掌握其沉降特征，进行了路基沉降监测，并利用尖点突变理论分析局部路基稳定性的现状。监测断面布置在成武高速第四标段C匝道，共布设两个监测断面，断面布置如图1所示，两断面水平间隔120 m；同时，每个监测断面共布置11个监测点，两断面的监测点布置情况图2所示。在监测过程中，监测频率为1次/周，监测项目为沉降监测。

图1 监测平面布置示意图

图2 监测断面布置示意图

根据现场监测，共获得21期(147 d)的监测数据。Ⅰ号监测断面的最大沉降量发生在6号监测点，沉降值为71.3 mm，位于监测断面中部；最小沉降量发生在1号监测点，沉降值为16.9 mm，位于路基靠边坡一侧。Ⅱ号监测断面的最大沉降量发生在7号监测点，沉降值为61.4 mm，位于监测断面中部；最小沉降量发生在1号监测点，值为26.4 mm，位于路基靠边坡一侧。

对两断面相应监测点的沉降变形进行对比，得到图3。由图3可知，路基沉降变形以中心处的沉降量相对更大，斜坡侧的沉降量相对较少，即路基沉降具不均匀特性；对比Ⅰ、Ⅱ监测断面在相应监测点处的沉降量可知，Ⅰ号监测断面的沉降量要略大于Ⅱ号监测断面的沉降量，说明随路基深度的增加，沉降量相应减小。

图3 两监测断面的沉降对比图

3.2 稳定性评价

根据路基填筑效果分析，得出路基整体稳定性满足设计要求，但因填料遇水易崩解等特性，在后期运营过程中，路堤内部填料因水的作用可能会出现崩解，导致局部的变形失稳。为进一步分析路基局部的稳定性特征，本文基于局部现场监测成果，以尖点突变理论中的突变特征值为评价指标，判断路基填筑后的稳定性。

尖点突变理论的研究重点是事物稳定与非稳定间的转换问题，对路基稳定性评价具有一定的适用性[13]。结合尖点突变理论的基本原理，先利用数值拟合来构建势函数，即采用Matlab拟合工具箱，对路基沉降数据进行四次多项式拟合：

Yt=a0+a1t+a2t2+a3t3+a4t4

(1)

式中：Yt——t时刻对应的拟合值；

ai(i=0，1，2，3，4)——拟合参数。

由于式(1)并非尖点突变理论的标准形式，需进行变换处理，且将变换方式确定为Tschirhaus变换，即令A=a3/4a4，t=x-A，并将其带入式(1)进行转化，得：

fx=b4x4+b2x2+b1x+b0

(2)

式中：fx——变换函数；

bi(i=0，1，2，4)——变换参数。

同时，参数a和b间存在如下矩阵变换关系：

(3)

对式(2)两侧同除b4，即可得到尖点突变理论的标准函数：

Ux=x4+μx2+vx+c

(4)

式中：Ux——标准函数；

μ、ν——突变特征参数。

两突变特征参数可根据下式进行求解：

(5)

(6)

基于两特征参数，可求得突变特征值：

Δ=8μ3+27v2

(7)

根据上述原理，提出以突变特征值为评价指标，判断路基沉降的稳定性，其判据为：当Δ<0时，路基处于不稳定状态；当Δ=0时，路基处于临界平衡状态；当Δ>0时，路基处于稳定状态。另外，当Δ>0时，Δ值可进一步评价路基的稳定程度，即Δ值越接近于零，稳定性越好[14]。

同时，在尖点突变分析过程中，选取两断面中沉降量最大的监测点为分析对象，即分析数据来源于Ⅰ号监测断面的6号监测点和Ⅱ号监测断面的7号监测点。

首先，对两监测点的所有监测样本进行尖点突变分析，以掌握其整体稳定性，且经Matlab的拟合工具箱拟合，得6号监测点的四次多项式拟合函数为：

yⅠ=-1.132×10-6t4+3.977×10-4t3-4.474×10-2t2+2.465t+1.812×10-13

根据拟合结果，6号监测点的拟合度为0.982 7，具较好的拟合效果，保证了后续分析的有效性。结合尖点突变理论的基本原理，对突变特征参数和特征值进行求解：

μⅠ=-4.351×104；νⅠ=-2.317×105

则

ΔⅠ=7.903×1011>0

根据上述计算，得到第Ⅰ断面6号监测点的突变特征值大于零，说明该监测点处于稳定状态。

类比上述，对第Ⅱ断面的7号监测点进行尖点突变分析，经拟合，得其四次多项式拟合函数为：

yⅡ=-8.808×10-7t4+3.193×10-4t3-3.951×10-2t2+2.124t+1.498×10-13

在7号监测点的拟合过程中，其拟合度为0.9879，较趋近于1，说明该监测点的拟合效果也较好。同时，也对该监测点的突变特征参数和特征值进行求解：

μⅡ=-4.423×103；νⅡ=-2.358×105

则

ΔⅡ=8.085×1011>0

根据计算结果，得到第Ⅱ断面7号监测点的突变特征值也大于零，说明该监测点也处于稳定状态。

对比两监测点的整体稳定性分析结果，得到两者均处于稳定状态，且ΔⅡ>ΔⅠ，说明6号监测点的稳定性相对更高。

其次，为掌握路基稳定性随时间持续的变化特征，再将监测样本划分为1-7周期、1-14周期、1-21周期三个阶段，并对各阶段进行尖点突变分析，结果如表5和6所示。

表5 6号监测点在不同阶段的稳定性分析结果

表6 7号监测点在不同阶段的稳定性分析结果

由表5和6可知，两监测点在不同阶段的突变特征值均大于零，说明路基始终处于稳定状态，且随时间持续，突变特征值不断减小，路基稳定性增加。

综合上述，整体分析和分阶段分析均得出路基处于稳定状态，验证了路基填料的适用性，为类似工程施工积累了经验。

4 稳定性发展趋势分析

通过构建粒子群优化极限学习机(PSO-ELM模型)来实现路基沉降的变形预测，进而判断路基稳定性的发展趋势[15-16]。极限学习机(Extreme Learning Machine，ELM)是一种新型智能模型，具有较高的学习速度和泛化能力，适用于非线性预测。若训练样本为(xi,ti)，且总个数为N，则可将极限学习机的网络模型表示为：

(8)

式中：yi——第i个节点处的预测值；

xi——第i个节点处的预测输入值；

K——隐层节点数；

g(x)——激励函数；

βi——隐层与输出层间的连接权值；

wi——输入层与隐层间的连接权值；

bi——隐层偏置。

极限学习机在相应参数设置前提下，可实现预测结果到期望结果的零误差逼近，即

(9)

根据训练样本可构建N个方程，并将其表示为矩阵形式：

T=Hβ

(10)

式中：T——期望输出矩阵；

H——隐层输出矩阵；

β——权值矩阵。

上式可等价于求解H=βT的最小二乘解，即需求解β′矩阵：

β′=H+T

(11)

式中：H+——H矩阵的广义逆矩阵。

在极限学习机的应用过程中，隐层节点数一般小于训练样本数，易造成复共线性问题，进而导致输出结果的随机波动，造成预测结果的稳定性不足。因此，为克服上述问题，该文提出利用粒子群算法优化极限学习机的权值矩阵和隐层偏置。

粒子群算法可将寻优参数看作为空间粒子的属性，通过不断迭代来更新粒子速度和位置，进而得到寻优目标的全局最优值。结合该文实例特点，将权值矩阵和隐层偏置的优化过程分述如下：

①随机产生一个粒子群，并对群中每个粒子赋予参数属性，即将权值矩阵和隐层偏置作为粒子属性，并将种群规模设置为30，惯性权值设置为1，学习因子设置为2，最大迭代次数为600 次，实现了粒子群的初始化。

②按下式求解各粒子的适应度值：

(12)

式中：fi——第i个粒子的适应度；

f(xi)——第i个节点处的预测值；

yi——第i个节点处的样本值。

③以适应度最小为原则，对比粒子群中所有粒子的适应度值，确定其中的最佳粒子。当最佳粒子的适应度值满足期望要求时，则停止迭代，最佳粒子的属性参数即为最优权值矩阵和隐层偏置；反之，改变粒子的位置和速度，并重新求解粒子的适应度值，直至达到期望值或达到设定的迭代次数。

在预测过程中，对Ⅰ号监测断面的6号监测点和Ⅱ号监测断面的7号监测点均进行预测。将训练样本设置为1～17周期，18～21为验证样本，且对22～24周期进行外推预测。通过预测，得两监测点的预测结果如表7～8所示。

表7 6号监测点的预测结果

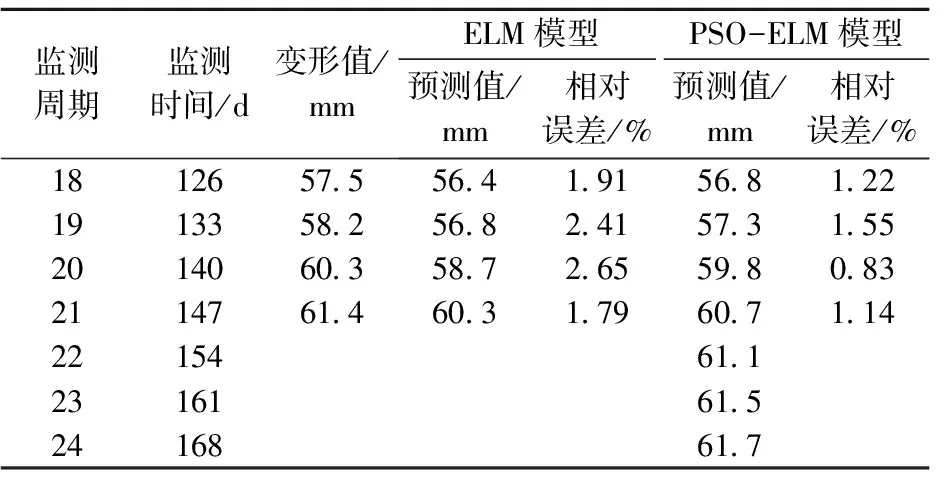
表8 7号监测点的预测结果

对比优化前后各监测点在相应节点处的预测效果可知，经粒子群算法的参数优化，有效提高了预测精度，验证了参数优化的有效性和必要性；在6号监测点的最终预测结果中，最大相对误差1.26 %，最小相对误差为-1.02 %，平均相对误差0.57 %，预测精度较高，满足期望要求，且外推预测表明，该监测点的变形值将会继续增加，但增加速率较小，趋于稳定；在7号监测点的最终预测结果中，最大相对误差1.55 %，最小相对误差为0.83 %，平均相对误差1.18 %，也具有较高预测精度，进一步验证了该文预测模型的有效性，且其外推预测变形值也呈小速率增加趋势。

根据上述，得出路基变形仍将进一步增加，但增加速率均较小，说明路基变形趋于稳定，且其稳定性发展趋势也趋于稳定。