运用地下水对潮汐的响应识别压力传导系数

阳 玲，杜金月，王同科，赵志学，郝永红

(1.天津师范大学数学科学学院，天津 300387；2.天津师范大学天津市水资源与水环境重点实验室，天津 300387)

世界上有40%的人口居住在离海岸线100 km以内的海滨城市，给近海海域带来了大量污染，破坏了生态环境[1-3]。源于陆地的海洋污染有44%是来自于地下水海底排泄和地表径流[1]。虽然地下水海底排泄的流量是地表河流入海径流量的40%[2]，但是它的污染物浓度却是地表径流的10倍[3]。海底地下水排放被视为海洋污染最主要的方式之一[4-5]。预测海底地下水排放和输送到海洋中的污染物对海洋生态和环境保护有着重要意义。

水文地质参数识别又称水文地质逆问题求解，是建立地下水数值模型的关键步骤[6]。含水层的压力传导系数作为描述地下水溶质运移的关键参数被广泛的研究[7-10]。传统识别压力传导系数最广泛的技术是抽水试验和振荡试验[11-13]，但是这些方法有一个共同的缺点：需要耗费大量的人力、财力和物力。为了更好地描述含水层的特性，有必要开发一种经济高效的方法来估计含水层的压力传导系数。

海洋和河流的潮汐可以看作自然的振荡抽水试验，可通过分析潮汐和地下水响应关系估计压力传导系数。Ferris估计了潮汐河含水层的压力传导系数，他使用了时间滞后和潮汐与地下水位相关的潮汐效率因素的方法[14]。Erskine估计了非承压和高度渗透沿海含水层的压力传导系数，该含水层位于英国的一个核电站附近，他用了时间滞后和潮汐效率因素方法[15]。Zhou利用观测井观测地下水水位振幅和潮汐确定了T/S(给水度与导水系数之比),写出了T/S的表达式[16]。在贝尔港沿海岩溶含水层的背景下，类似的压力传导系数的估计表明，水动力环境包括基质、裂隙和管道流动系统。

然而，前人运用地下水水位对潮汐的响应识别含水层的参数多采用数值拟合的方法。在前人的研究基础上，本文试图获得潮汐产生的压力波在含水层中传播的解析解，通过数值拟合估计含水层的压力传导系数。其能够更加清楚地了解潮汐影响地下水的机理。

1 地下水模型

假设海滨区有一个水平、均质、等厚的含水层，它位于两弱透水层之间(图1)。因为地下水的压力水头高于含水层和海水的高度，所以地下水向海中排泄。

基于图1的概念模型，建立笛卡尔直角坐标系，x轴的原点位于内陆，距海岸的水平距离为l m，且地下水水位是定水位H1。x轴是水平的，沿着含水层向海岸方向延伸，垂直方向为海岸线方向。在实际条件中左边界为定水位边界的可能性不大，更多的是流量边界。假设有一条与海岸平行的运河，保证左边界为定水位边界。该模型需假设有一条与海岸平行的运河，且该运河与海不相通。

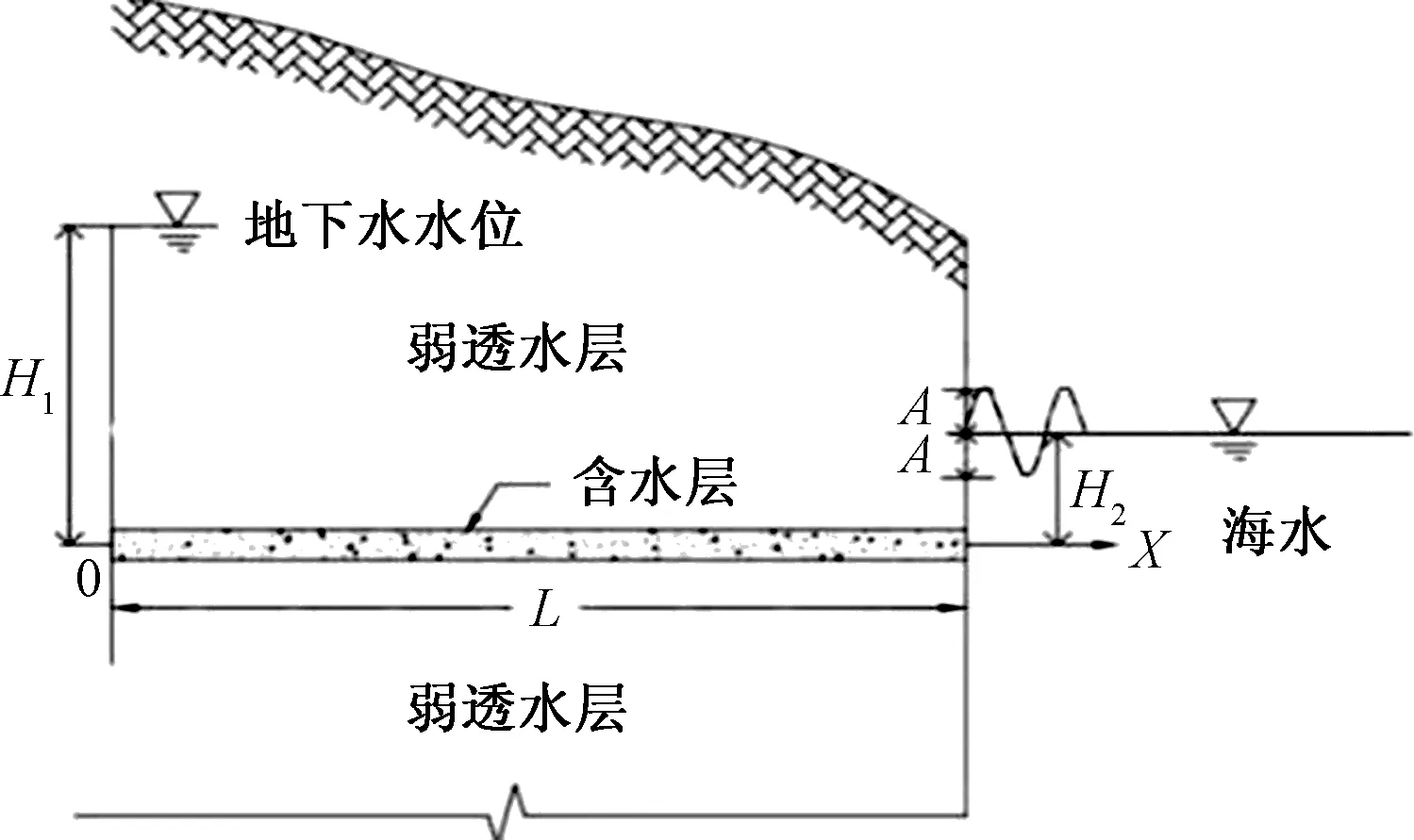
图1 滨海区含水层概念模型

承压含水层中地下水运动的一维偏微分方程为：

(1)

式中：H——水头/m；

x——水平坐标/m；

t——时间/h；

T——含水层的渗透系数/(m·h-1)；

S——含水层储水系数；

l——含水层的长度/m。

(2)

边界条件为：

H|x=0=H1，H|x=l=H2+Asinωt，t>0，

(3)

式中：H1——内陆含水层定水头边界/m；

H2——海水平均水位/m；

A——海水振荡振幅/m；

ω——角速度/h-1。

2 地下水位对潮汐响应的解析解

将式(2)～(3)转化到复数域上[17-18],即将有关物理量从实平面扩充到复平面[19]。变量x和t是相互独立的。因此可以用分离变量法求解：

H(x,t)=u1(x,t)+u2(x,t)

(4)

(5)

将式(4)代入式(1)～(3)中：

(6)

u2(0,t)=0,u2(l,t)=Asinωtt>0

(7)

因为式(7)关于时间是周期的，所以可以省略初始条件。把式 (4)～ (6)扩张到复数域，假设u2(x,t)=lm(U(x,t)),代入式(6)～(7)，可以得到：

(8)

U(0,t)=0,U(l,t)=Aeiωt,t>0

(9)

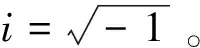
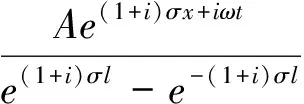
(10)

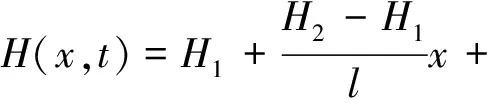
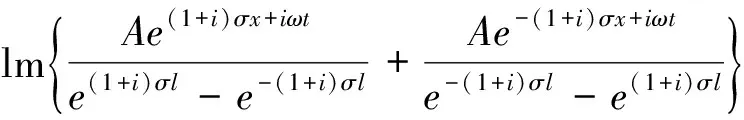
(11)

最终求解结果：

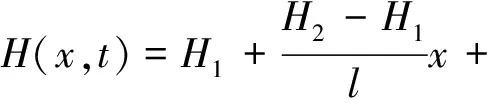
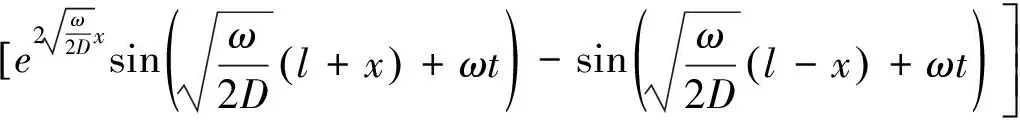
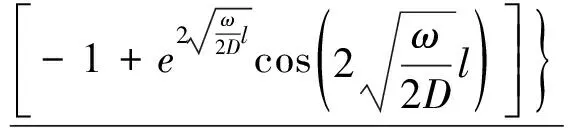
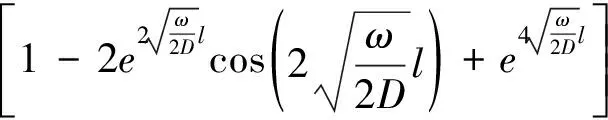
(12)

式(12)可以简化为：

(13)

其中：

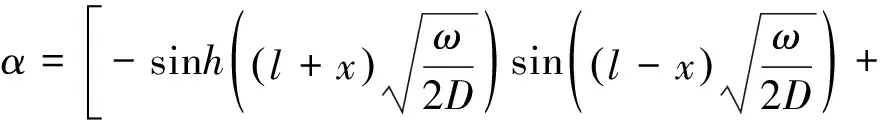
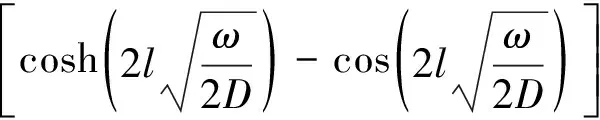
(14)

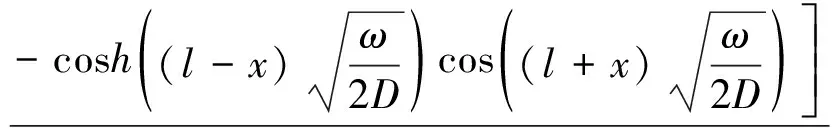
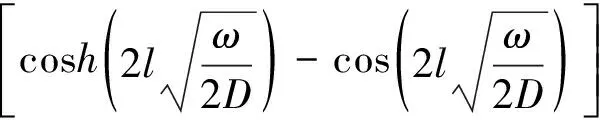
(15)

3 识别含水层的压力传导系数

(16)

(17)

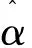
4 数值仿真

为了验证潮汐信号衰减率方法的正确性，了解该方法的精度，对式(13)中的参数赋值(表1)，进行了数值仿真。赋值后由式(13)获得的地下水水位对潮汐的响应图，见图2。

表1 含水层参数

图2 地下水对潮汐的响应

为更加清晰地了解不同位置地下水响应情况，图3表达了x=30 m和x=80 m以及海水水位三种不同情况下地下水水位随时间的变化。

图3 x=30 m和x=80 m以及海水水位三种不同情况下地下水位随时间的变化

为检验潮汐衰减率r(x,t,ω)与余切函数cotωt之间的线性关系。当x=80 m时地下水水位，r(x,t,ω)与cotωt呈线性相关(图4)。

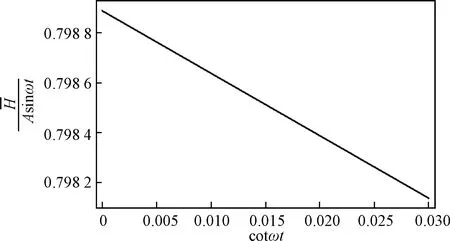
图4 x=80 m时r(x,t,ω)与cotωt的线性关系

为了验证潮汐信号衰减率方法的正确性，模拟野外地下水水位的观测过程，对x=80 m处的地下水数据进行取样，取样时间步长为15 min，共获得48个采样点(图5)。

由图6可见，r(80,t,ω)与cotωt呈线性关系。由于采样步长15 min，相对于样本总体时间较小，图6中部分点重合。

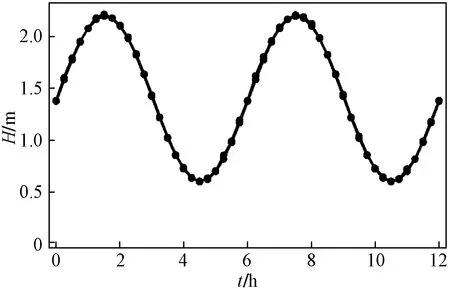
图5 在x=80 m处，时间间隔为0.25 h,地下水对潮汐响应的合成数据

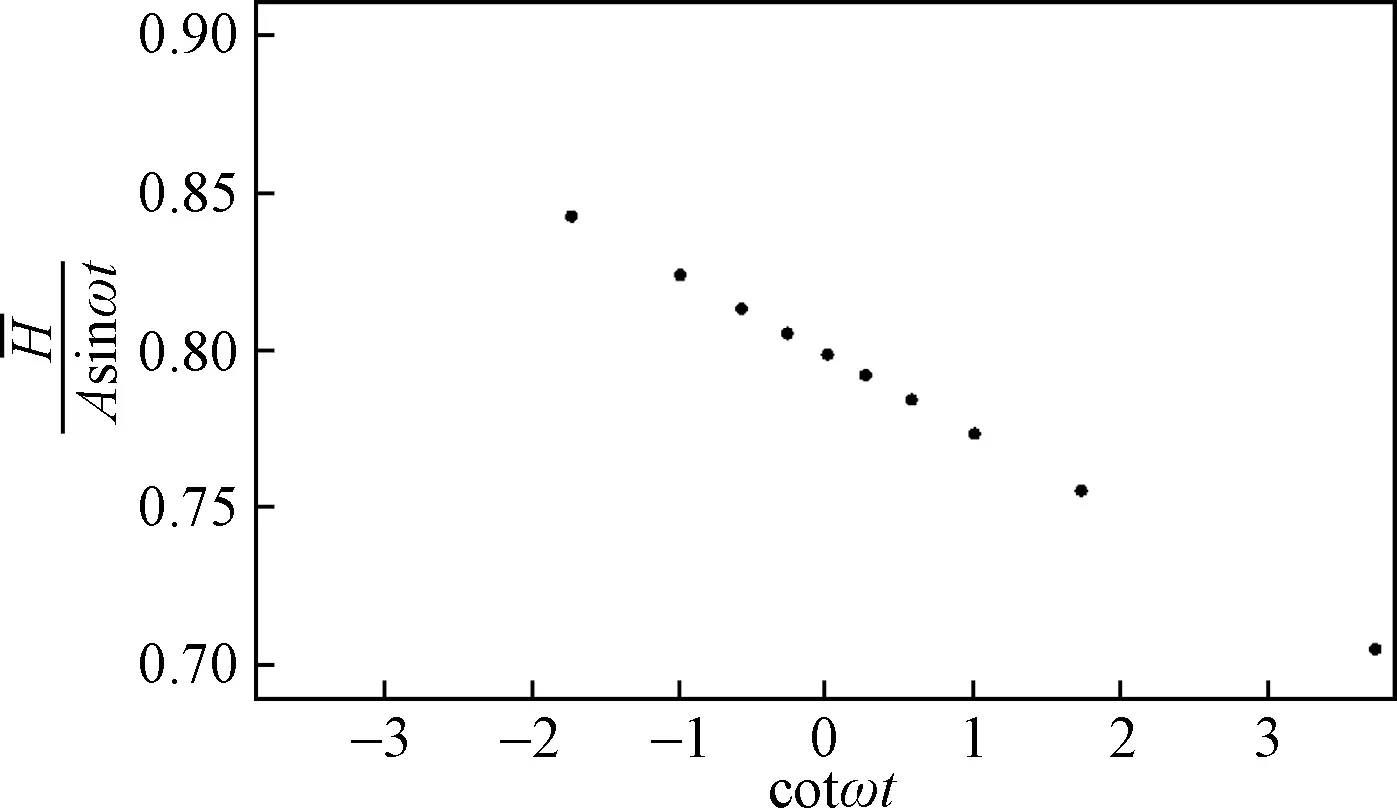
图6 潮汐信号衰减率r(x,t,ω)与cotωt的线性关系

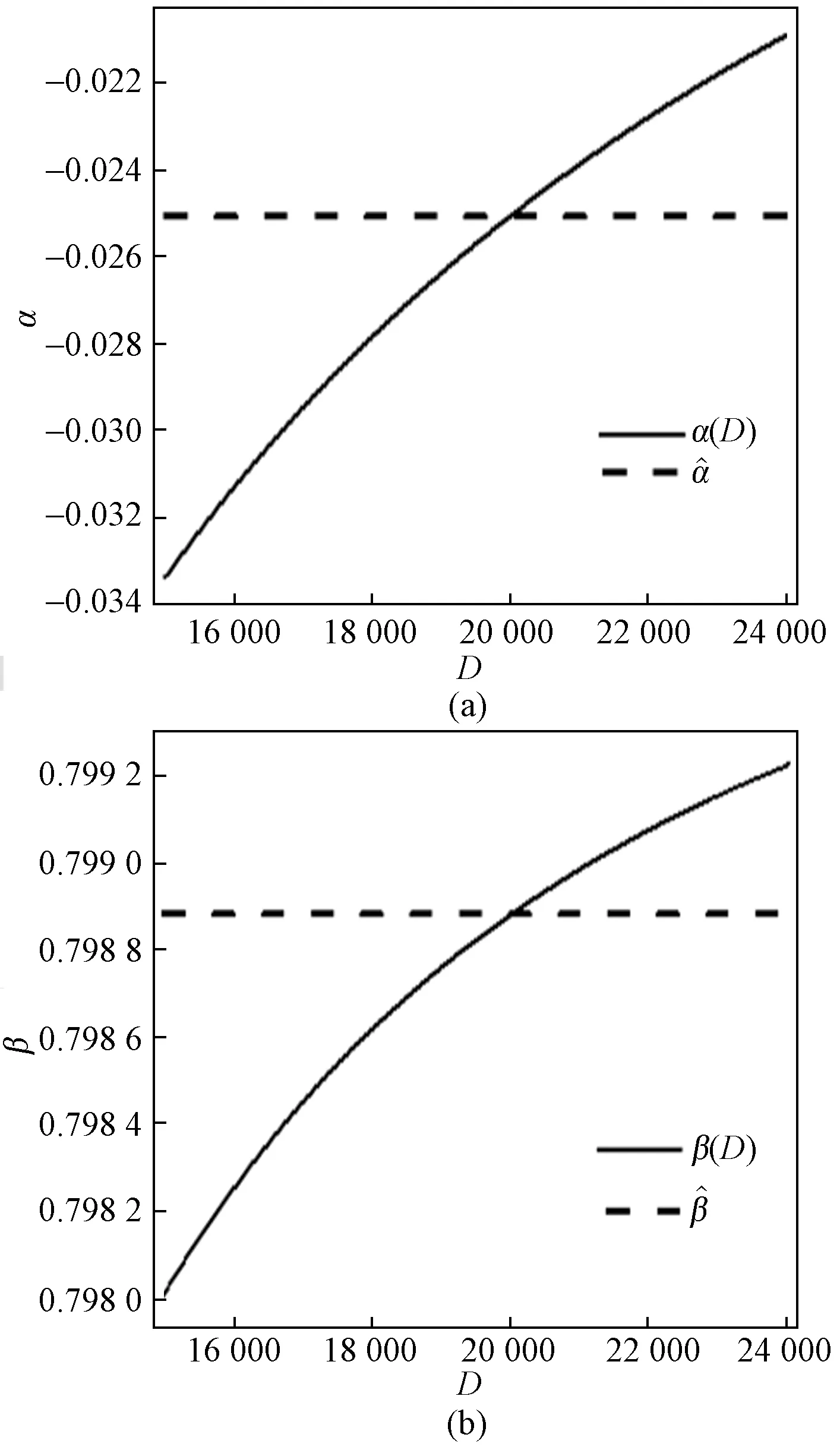
图7 用α和β估计初值

5 结论

(1)在滨海含水层中，地下水水位与海洋潮汐的交互作用类似于自然的振荡抽水试验。当涨潮时，相当于给地下水注水，地下水水位上升。当退潮时，相当于抽取地下水，地下水水位下降。基于潮汐信号在含水层中传播和衰减的过程，建立地下水模型求得解析解，提出用潮汐信号衰减率方法估计含水层的特性。潮汐信号衰减率r(x,t,ω)与海水振荡的余切函数cotωt线性相关。

(2)线性关系中的斜率和截距都是压力传导系数的函数。提出了利用潮汐信号衰减率与余切函数的关系估计压力传导系数的方法(即用斜率和截距估计压力传导系数)。数值仿真结果表明，该方法可以准确地估算含水层的压力传导系数D。

(3)潮汐衰减率方法具有少打井，经济高效等优点，但也存在一定的局限性。在一般情况下含水层长度l值的获取需要一定的工作量，在实际应用中需要根据情况权衡。