压实黄土水分入渗规律及渗透性试验研究

张镇飞，倪万魁，王熙俊，苑康泽，潘登丽，刘 魁

(1.长安大学地质工程与测绘学院，陕西 西安 710054；2.信息产业部电子综合勘察研究院，陕西 西安 710000)

黄土具有大孔隙、垂直节理发育以及水敏性等特点。通常经过碾压、夯实或振动压实等方法处理后，黄土作为一种建筑材料直接运用到工程建设中。黄土地基的湿陷变形及其他岩土工程问题都与压实黄土中水分入渗规律及渗透特性密切相关[1]。

目前，用来描述土中水分入渗规律的理论模型主要有Green-Ampt物理模型、Horton经验模型、Philip物理模型[2]和Kostiakov经验模型等。同时，许多学者在黄土地区也开展了大量的探索研究，蒋定生等[3]提出了积水条件下黄土入渗率经验公式；王全九等[4-5]分析了水平入渗中水分运动参量之间的关系，并建立了Green-Ampt模型与Philip模型参数间的联系；王文焰等[6]推导出适合黄土区的Green-Ampt入渗模型公式；王念秦等[7]对原状离石黄土的向上渗流规律进行了研究。此外，黄雪峰等[8]、安鹏等[9]在黄土地区进行了不同规模的现场浸水试验，对探索黄土中水分入渗规律研究起到巨大的推动作用。

实际中，由于非饱和压实黄土中基质吸力的存在，其渗透特性远比饱和土复杂。压实黄土的饱和渗透系数接近于常数，而非饱和渗透系数是含水率(基质吸力)的函数[10]。目前，非饱和渗透系数通常由直接法或间接法得到。直接法是在试验室或现场通过渗透试验直接测得。其中，瞬时剖面法在直接法中较为常用，最先由Richard等[11]于1953年提出。之后，诸多学者在此基础上对试验装置和数据处理方法进行了大量改进研究，Hamilton等[12]利用水平渗透装置(不考虑水头梯度)测定了Goose湖黏土的渗透特性；王红等[13]利用土柱试验测定了重塑黄土的非饱和渗透系数；陶高梁等[14]利用土柱装置研究了不同干密度红黏土的非饱和渗透性；文杰等[15]通过原位入渗试验对黄土的非饱和渗透系数进行测定。由于非饱和渗透试验装置复杂，且试验持续时间较长，前人提出了诸多能够用土-水特征曲线和饱和渗透系数间接预测非饱和渗透系数函数的模型公式。其中，van Genuchten[16]、Fredlund等[17]渗透系数模型在岩土工程领域应用较为广泛[18]。叶为民等[19]利用Fredlund等渗透模型预测了上海软土的非饱和渗透系数；刘争宏等[20]利用van Genuchten渗透模型预测了安哥拉Quelo 砂场地非饱和土的渗透系数曲线。目前，针对压实黄土的非饱和渗透系数的直接测定和间接预测之间的系统研究还比较少。

本文以延安压实黄土为例，利用自主研制的渗透试验装置，先进行常水头入渗试验，观测压实黄土中水分入渗过程及变化规律，同时测定饱和渗透系数；再进行降雨入渗试验，采用瞬时剖面法计算压实黄土的非饱和渗透系数，同时测定土体土-水特征曲线。根据土-水特征曲线选用van Genuchten和Fredlund等渗透系数模型对非饱和渗透系数进行预测，并将模型预测值与瞬时剖面法实测值进行对比分析。

1 压实黄土常水头水分入渗规律

1.1 试验装置及过程

自主研制的土柱垂直入渗模型试验装置如图1所示，包括土柱装置和反力架两部分。土柱装置由有机玻璃试筒和钢底座组成，整体置于反力架底座上。试筒高63 cm，内直径30 cm，筒壁厚1 cm。筒壁两侧对称分布两列直径0.8 cm的圆形小孔，列向间距10 cm。试验时通过4根螺纹拉杆将试筒紧紧固定在钢底座上，并在结合处涂抹玻璃胶，防止漏水。土柱底座均匀布满直径5 mm的透水孔，其下为集水槽，通过排水管将水排出。

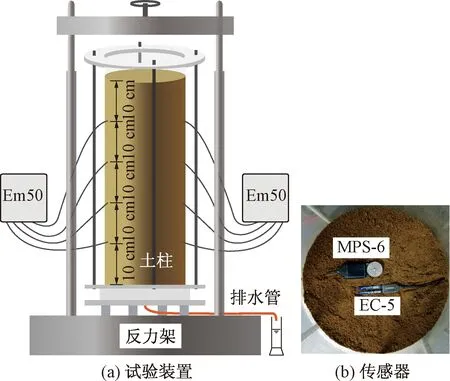
图1 试验装置示意图

此次试验土样取自延安某场地。利用激光粒度仪测得土样粒径级配累积曲线如图2所示。将土样风干碾碎，过2 mm筛，并配制成湿土样。装入密封桶内静置不少于72 h，并复测含水率。根据复测含水率、试筒截面积及目标干密度，计算出5 cm高土柱所需湿土质量。称取计算质量的湿土样，并均匀铺在试筒内，利用试验装置自带的加压设备将虚土压实至目标高度(5 cm)，压实过程中确保虚土受力均匀。重复上述操作，将土样分层压实，两层交界处土面刨毛，分别制成高50 cm干密度1.45 g/cm3和1.55 g/cm3的土柱，其初始含水率分别为12%和16%。土柱制作过程中分别在埋深10，20，30，40 cm处埋设1组EC-5水分传感器和MPS-6水势传感器。土柱制作完成后，待水分和水势传感器读数稳定后方可进行渗水试验。试验开始前调试并设置好Em 50数据采集器。试验时保持10 cm稳定水头，观察水分入渗过程并及时记录。当排水管有水流出，用量筒定时量测流出水量。渗流稳定后停止试验。

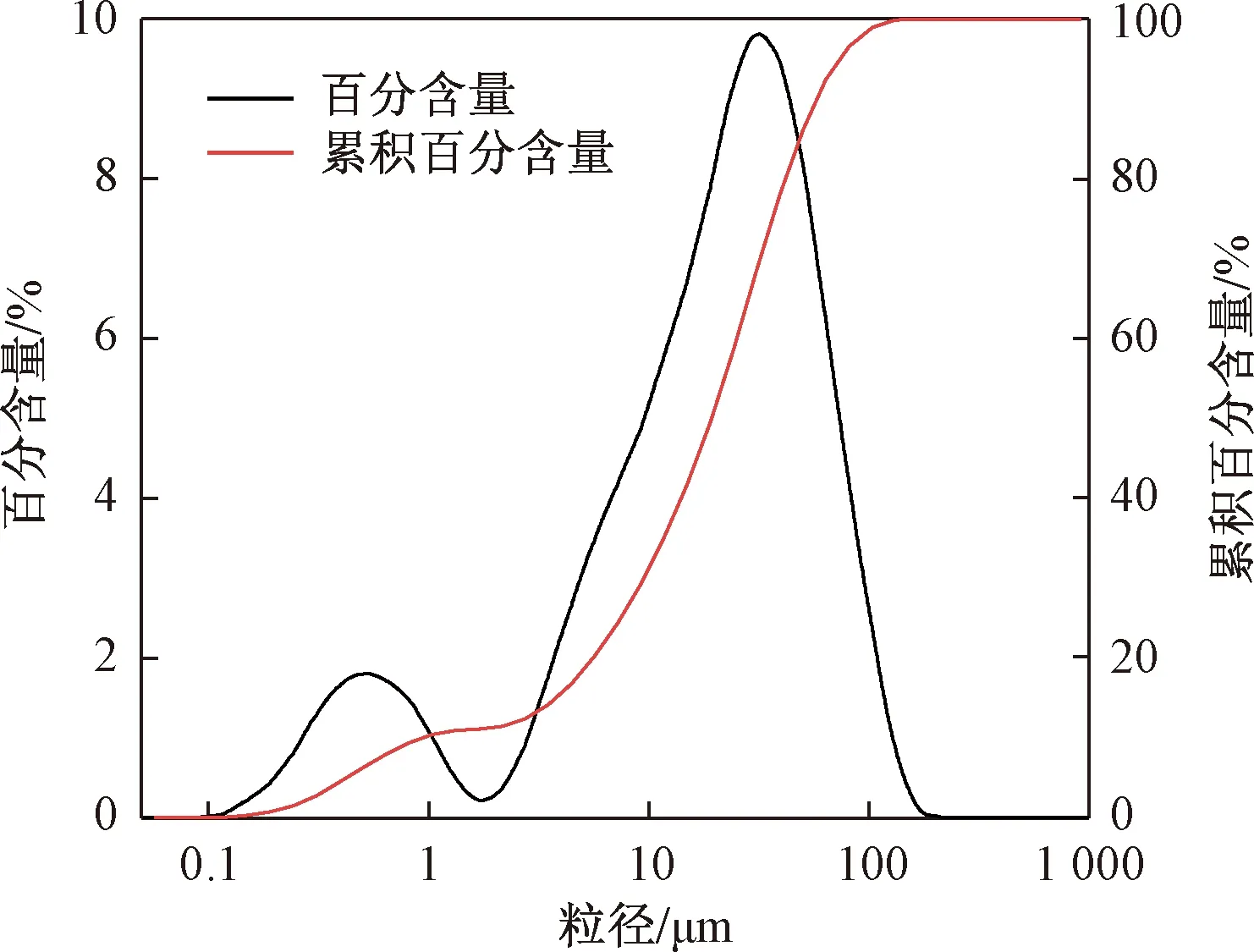
图2 土样粒径级配累积曲线

1.2 试验结果及分析

(1)累积入渗量及入渗率变化规律

分别建立2组试样累积入渗量及入渗率随时间的变化曲线(图3)。压实黄土的累积入渗量随入渗时间逐渐增加，根据土柱底部是否出水可将累积入渗量时间曲线分为2部分。在底部出水时间点之前，累积入渗量随入渗时间呈非线性增长(阶段一、二)，并采用Philip入渗模型对试验结果进行拟合分析，拟合结果见表1，2组试样累积入渗量随入渗时间均呈幂函数形式增长；在底部出水时间点之后(阶段三)，由于土柱被完全浸湿，土体接近于饱和状态，所以在此后阶段中累积入渗量与时间之间呈线性关系。

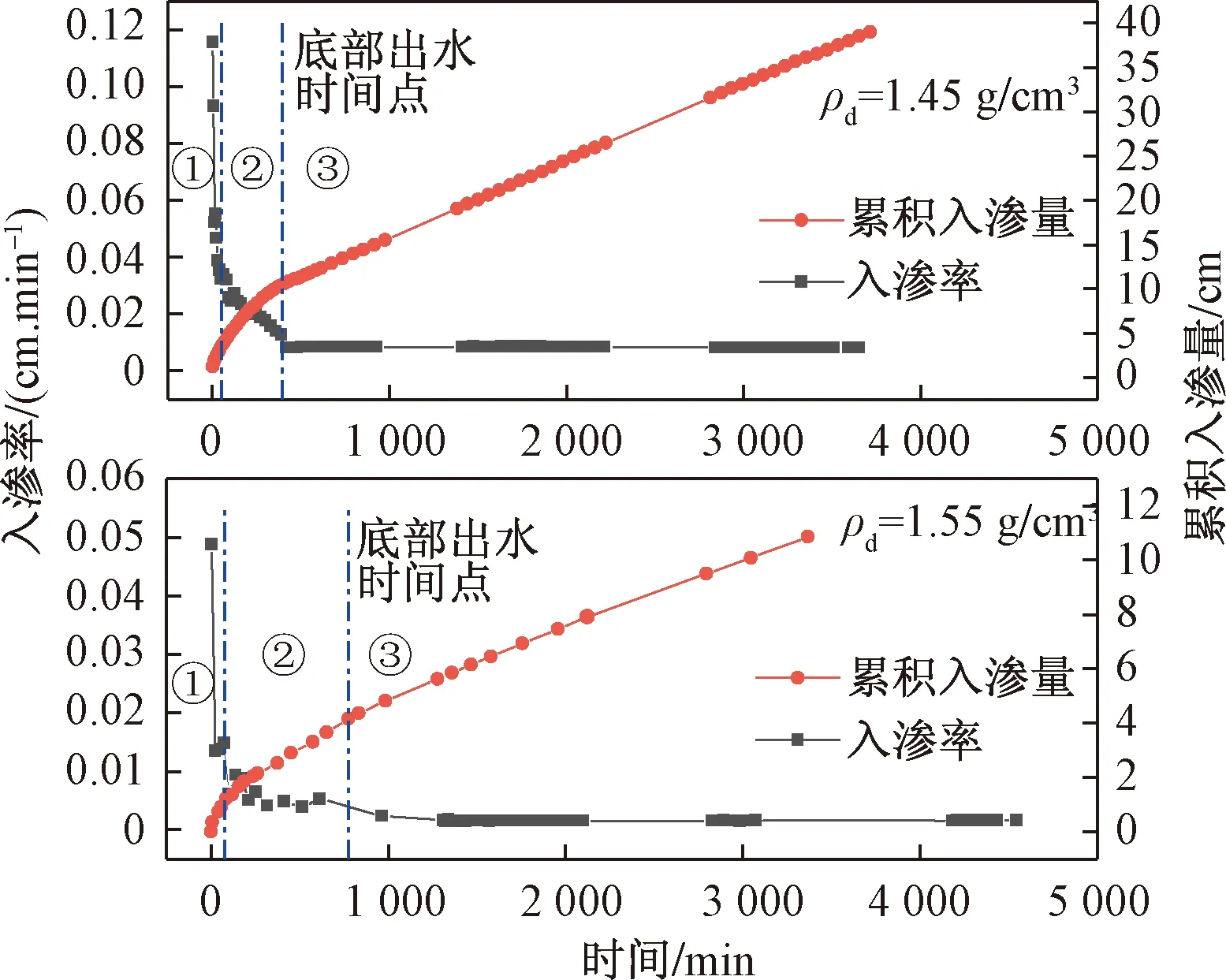
图3 累积入渗量及入渗率时间曲线

表1 累积入渗量与时间的拟合关系式

注：Q—累积入渗量/cm；t—入渗时间/min

从图3中可以看出，入渗率随入渗时间快速降低并最终趋于稳定。以干密度ρd=1.45 g/cm3土柱试验结果为例，入渗率变化过程可大致划分为3个阶段。第一阶段发生在入渗初期(0～55 min)，土体入渗能力强，入渗率变化幅度大，在入渗开始时最大，随时间的推移呈直线下降趋势；55 min之后，以底部出水时间点(395 min)作为第二阶段和第三阶段的分界点，在55～395 min时间段内入渗率随时间呈逐渐减小趋势；底部出水时间点以后为第三阶段，入渗率几乎不再发生变化，基本稳定在8.46×10-3cm/min，达到稳定渗流状态。饱和渗透系数可通过稳定渗流阶段计算得到，其值为ks=1.175×10-4cm/s。干密度ρd=1.55 g/cm3试样入渗率最终基本稳定在1.54×10-3cm/min，饱和渗透系数ks=2.134×10-5cm/s。

图4 湿润锋前进距离时间曲线

(2)湿润锋前进特征

随着入渗时间的增加湿润锋不断前移，湿润锋前进距离时间曲线的斜率为湿润锋前进速率，通过计算可得到整个入渗过程中湿润锋前进速率与时间的关系曲线(图4)。从图4中可以看出，从开始出现湿润锋到土柱完全浸湿的整个过程中，湿润锋前进速率呈持续减小趋势，并最终趋于稳定。可用幂函数方程描述湿润锋前进距离与入渗时间的关系(表2)。

表2 湿润锋前进距离与时间的拟合关系式

注：Z—湿润锋前进距离/cm

(3)湿润锋前进距离与累积入渗量、入渗率的关系

由图5可看出，累积入渗量与湿润锋前进距离之间呈线性关系，可用过原点的直线公式进行拟合。入渗率随湿润锋前进距离的增加呈反比例函数形式降低，即与湿润锋前进距离的倒数呈正比(表3)。

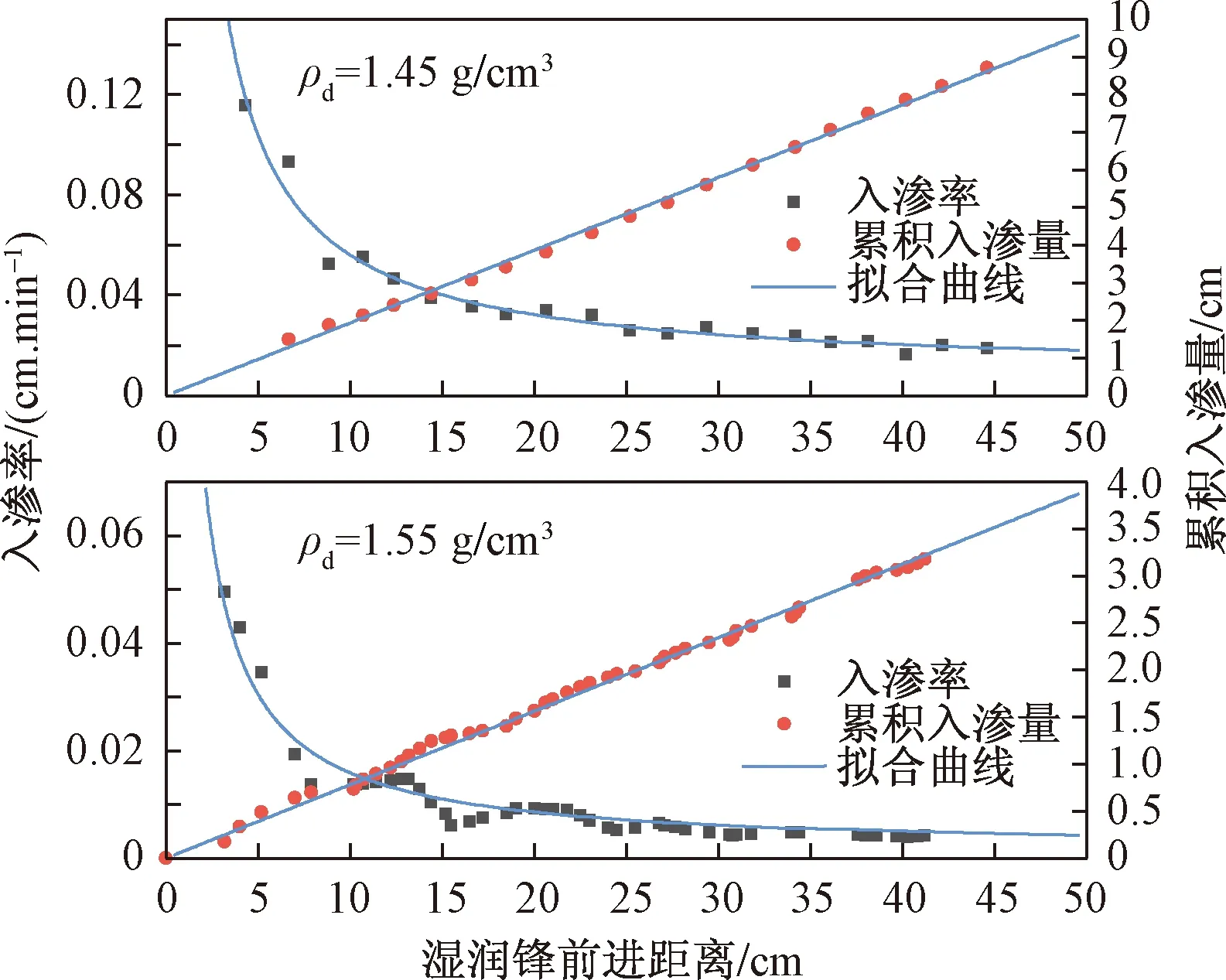
图5 湿润锋前进距离与累积入渗量、入渗率关系曲线

表3 湿润锋前进距离与累积入渗量、入渗率拟合关系式

注：q—入渗率/(cm·min-1)。

(4)含水率及基质吸力变化规律

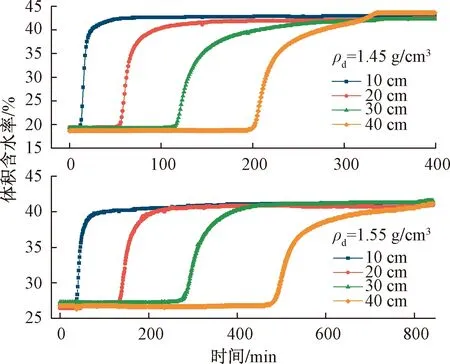
图6 不同埋深处土体含水率时程曲线

如图6所示，随着入渗的进行，10～40 cm埋深处的水分传感器读数均依次表现为突然升高并最终趋于平稳。不同埋深处土体体积含水率最终趋于一致，干密度1.45 g/cm3和1.55 g/cm3试样的体积含水率最终稳定在43%和41%左右。而实验室抽气饱和法实测饱和体积含水率分别为47.66%和45.77%，试验中土体最终接近饱和状态，但没有达到完全饱和。另外，2组试验结果都表现出水分传感器埋深越大，体积含水率曲线稳定过程越缓慢，这是因为随着入渗的进行，入渗率逐渐减小。土体埋深越大，水分到达时间也越久，入渗率也就越小，使土体饱和的时间也就越长。所以，埋深较大土体的饱和过程相对埋深较浅处土体也越长，反映在体积含水率曲线上则表现为增长缓慢。

基质吸力随时间的变化规律则表现为与体积含水率正好相反(图7)，表现为10～40 cm埋深处的水势传感器读数依次出现骤减并最终趋于稳定。当水分前进至水势传感器位置处，基质吸力急剧下降。随着水分的继续迁移，土体含水率逐渐增大至接近饱和。基质吸力值最终稳定在13 kPa左右。

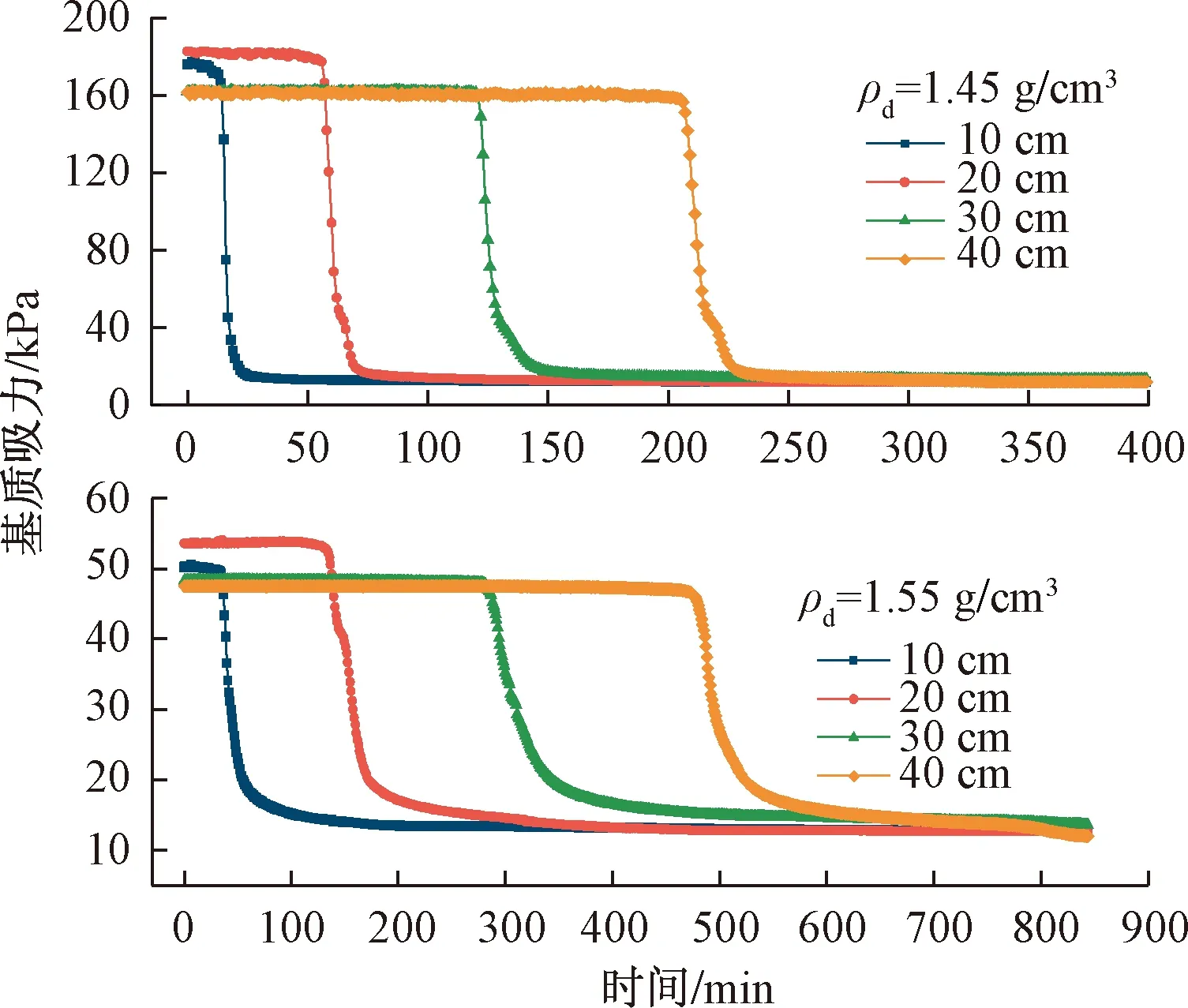
图7 不同埋深处土体基质吸力时程曲线

2 压实黄土渗透系数测定与模型预测

2.1 瞬时剖面法测定非饱和渗透系数

土柱制备同常水头入渗试验，制备初始含水率12%、干密度分别为1.45 g/cm3和1.55 g/cm3的2组土柱试样。待水分和水势传感器读数稳定后，用洒水器模拟降雨过程，向土柱表面持续均匀洒水30 min，累积加水量4 400 mL。洒水前在土柱顶面铺设10 cm厚玻璃珠，防止在入渗过程中发生土体表面板结或沿侧壁集中入渗，尽量保证水分入渗均匀。洒水结束后迅速取出玻璃珠并用保鲜膜覆盖土柱表面，同时用直径30 cm的薄塑料板压紧保鲜膜，防止水分蒸发。

根据上述监测的体积含水率和基质吸力值，绘制出体积含水率的时空变化剖面(图8)。入渗过程中任意位置zj的总水头hw等于该点的位置水头zj和基质吸力水头hm两者之和(不考虑渗透压力水头的作用)，即：

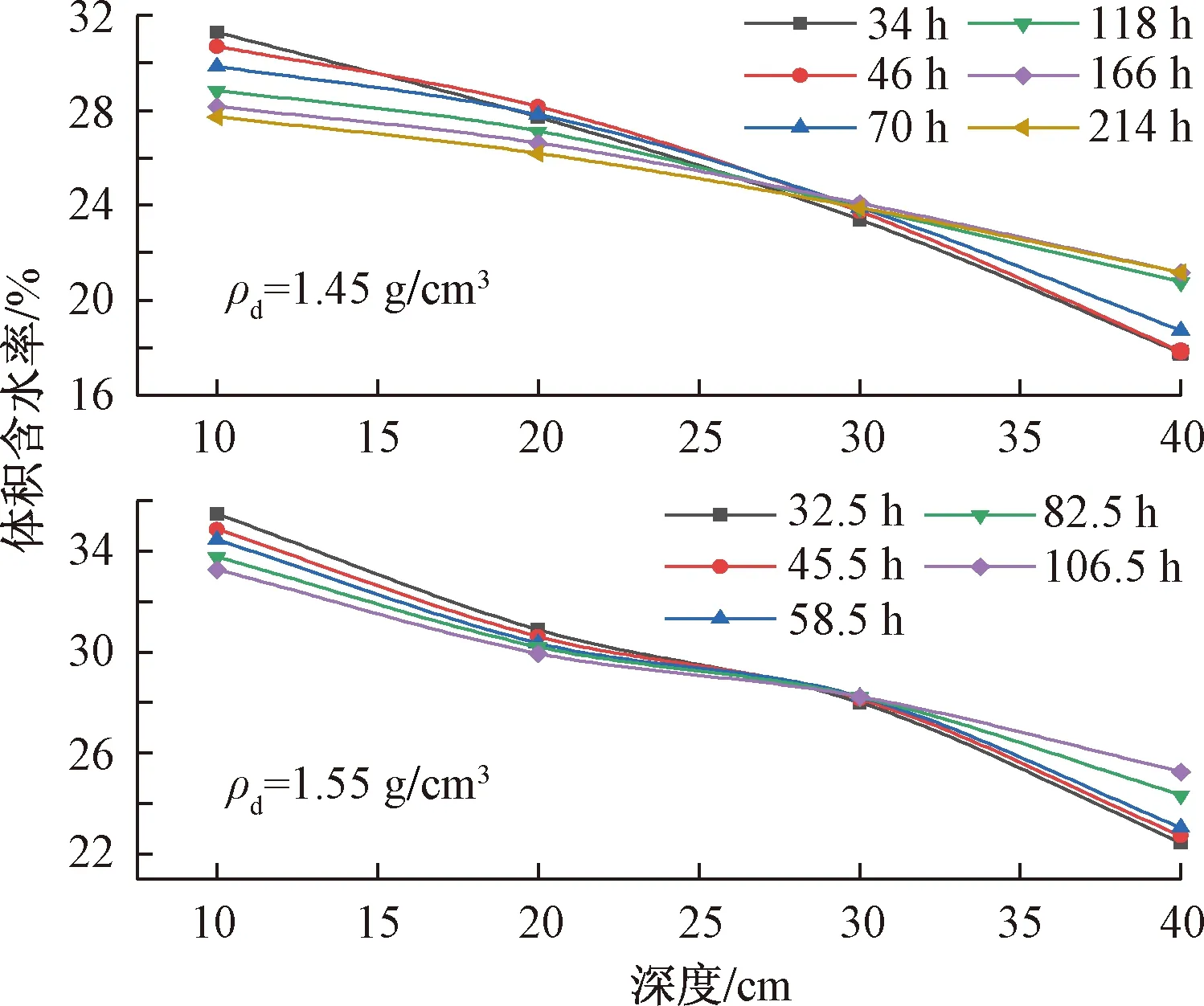
图8 体积含水率的时空变化剖面

(1)

t时刻zj处水力梯度iw等于该点水头分布线的斜率，即：

(2)

zj处与土柱顶面之间水的总体积Vw可由该时间内实测体积含水率时空变化剖面积分得到：

(3)

式中：Vw——zj处与零流量界面(土柱顶面)之间土的总水量；

A——土柱的截面面积/(cm2)；

θw(z)t——t时刻的体积含水率。

θw(z)t是深度z的函数，可在图8中的体积含水率剖面采用三次样条曲线拟合得到。

在时间间隔dt内流过zj点的水量，等于dt时间内计算的通过zj点的水体积变化量dVw。则该点的流速vw可表示为：

(4)

非饱和土的渗透系数为渗透流速与平均水力梯度的比值，即：

kw=-vw/iave

(5)

式中：iave——选取时间内该点的平均水力梯度。

计算iave时采用向前差分法，即：

(6)

式中：hw(j),t——t时刻zj处的水头值。

根据公式(1)～(6)可得到压实黄土非饱和渗透系数随体积含水率的变化曲线(图9)。对实测试验数据点进行拟合，得到非饱和渗透系数与体积含水率的关系式(表4)。结果表明，压实黄土非饱和渗透系数随体积含水率增大呈指数增长。干密度ρd=1.45 g/cm3试样的体积含水率在20 %和30 %之间变化时，相应的渗透系数在4.3×10-9～5.6×10-7cm/s范围内变化。干密度ρd=1.55 g/cm3试样试验结果位于4.1×10-9～ 1.7×10-7cm/s范围(含水率区间为25 %～35 %)。非饱和渗透系数值均跨越了2个数量级，且其数值远小于饱和渗透系数。

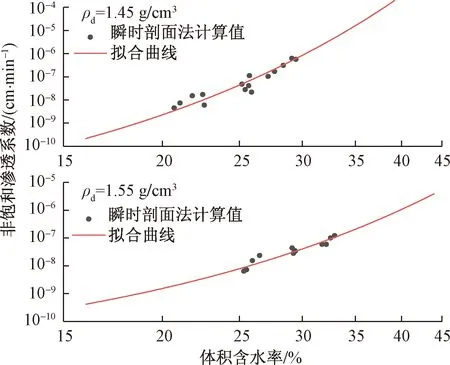
图9 瞬时剖面法计算的非饱和渗透系数及拟合曲线

表4 非饱和渗透系数与体积含水率的拟合关系式

2.2 土水特征曲线

在土柱同一位置处埋设水分和水势传感器，可实时量测该点土体体积含水率和基质吸力值。目前，国内外学者已经提出多种模型来反映含水率和基质吸力的关系。其中使用较广泛的为van Genuchten(VG)模型[16]和Fredlund-Xing(FX)模型[21]。

van Genuchten模型：

(7)

式中：θs——饱和体积含水率；

θr——残余体积含水率；

ψ——基质吸力/kPa；

A，m，n——拟合参数，m=1-1/n。

Fredlund-Xing模型：

(8)

(9)

式中：C(ψ)——修正因子；

ψr——残余含水率状态时的吸力值/kPa。

通过试验发现，埋深10 cm处传感器读数较其他位置处变化范围更大。故采用上述两模型对该位置处传感器监测数据进行拟合处理，得到完整的土-水特征曲线(图10)，拟合参数如表5所示。试验中实测基质吸力主要集中10～200 kPa范围内，两种模型的拟合曲线在此区间内高度重合，决定系数均大于0.995，两模型模拟压实黄土土-水特征曲线的效果都很好。

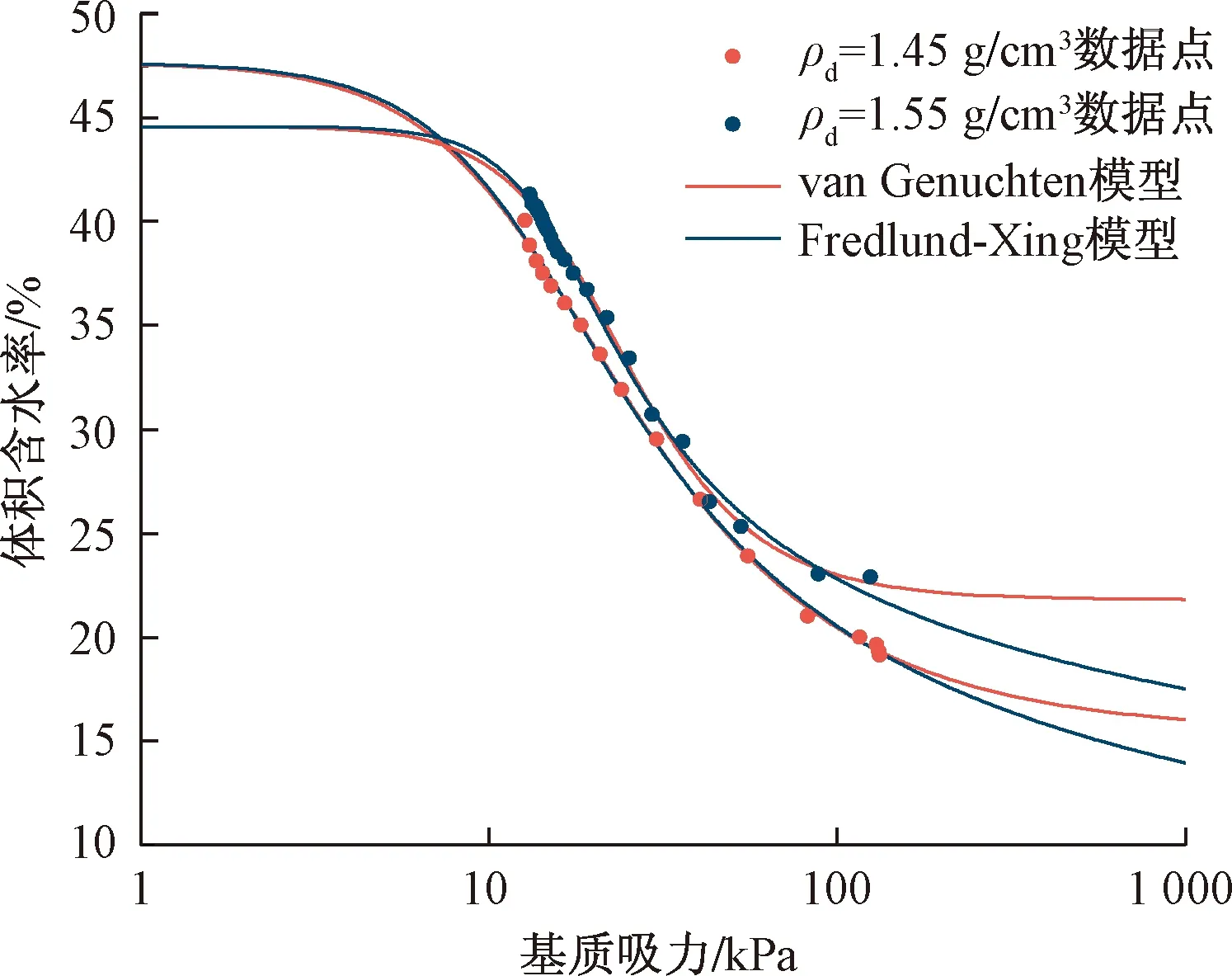
图10 VG模型和FX模型模拟的土-水特征曲线

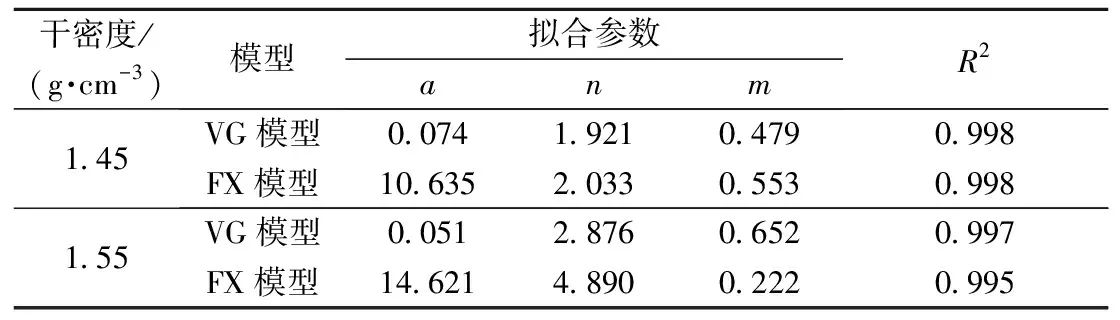
表5 VG模型和FX模型模拟土-水特征曲线拟合参数

2.3 土-水特征曲线预测非饱和渗透系数函数

非饱和土渗透系数模型众多，其中统计模型可根据土-水特征曲线间接预测非饱和渗透系数。本文采用van Genuchten和Fredlund等渗透系数模型对压实黄土渗透系数进行预测。

van Genuchten渗透系数模型：

(10)

Fredlund等渗透系数模型：

(11)

式(11)中积分项可用如下数值积分进行计算，定义a和b分别为积分的下限和上限，则：

a=ln(ψaev)，b=ln(106)

(12)

将区间[a,b]等分为N段，每段区间长度为Δy，则：

(13)

式(11)可改写为：

(14)

式中：ψaev——进气压力值；

y——积分ln(ψ)的虚变量；

θ′——公式(8)对ψ的导数；

Θq——考虑曲率的修正系数(q=1)；

考虑整个基质吸力范围内土-水特征曲线时，含水率小于残余含水量时标准化体积含水率出现负值，此时，标准化体积含水率等于饱和度，即Θ=θ/θs。虽然式(11)中进气值作为积分下限，但在0和进气值ψaev之间任何值都可以使用。所以不必知道精确的进气值[17]。

将表5中的拟合参数和常水头入渗试验测得的饱和渗透系数ks带入式(11)中，即可得到非饱和渗透系数函数曲线，计算结果如图11。两种统计模型预测的渗透系数函数曲线形态在低吸力值处差别不大，但随着基质吸力(含水率)的增大(减小)差异越来越大。以干密度ρd=1.45 g/cm3的土柱试验结果为例分析，当基质吸力较小(ψ<8 kPa)时，其饱和度大于85 %，土体中孔隙的体积主要被水占据，渗透系数相对较高，其值接近饱和渗透系数。但随基质吸力继续增大到一定程度后，渗透系数开始变小，因为随基质吸力的增大，饱和度持续减小，气体逐渐进入到土体孔隙中，土中水分运移动力主要是重力梯度和基质吸力梯度，受到基质吸力的影响也越来越大。在实测基质吸力30～100 kPa区间内，用瞬时剖面法计算的压实黄土非饱和渗透系数主要位于10-9～10-7数量级区间，Fredlund等渗透系数模型预测值位于10-8～10-6区间，预测结果较实测值偏大，而van Genuchten渗透系数模型预测值和瞬时剖面法实测值数量级区间相一致，且实测值和预测值重合度也较高，预测效果更好。

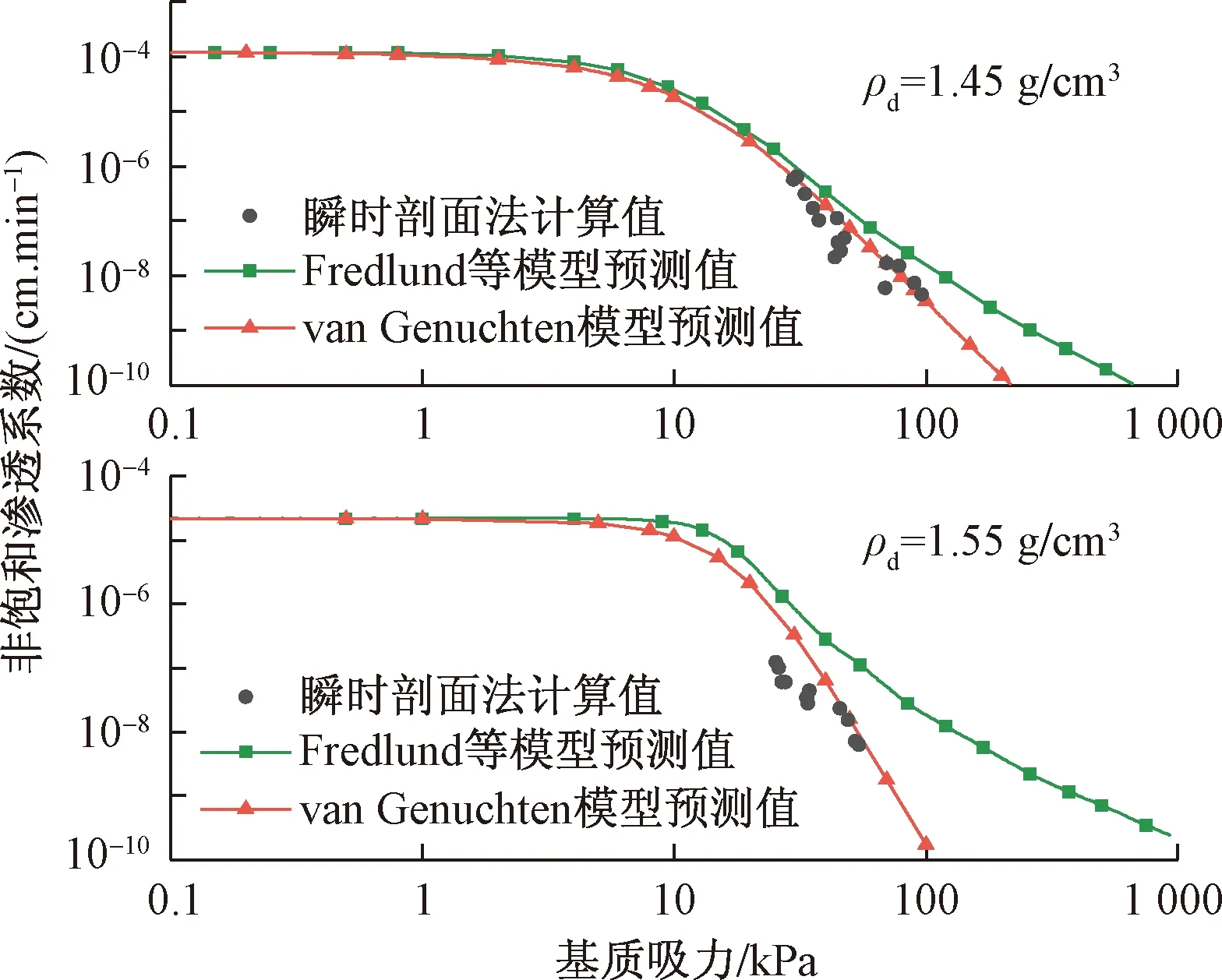
图11 非饱和渗透系数实测值与预测值对比

3 结论

(1)通过土柱常水头入渗试验，建立了压实黄土累积入渗量、湿润锋前进距离、入渗率以及入渗时间之间的函数关系。

(2)利用水分和水势传感器直接量测增湿过程中土体体积含水率和基质吸力值，得到了压实黄土的土-水特征曲线。同时，利用瞬态剖面法测定ρd=1.45 g/cm3试样的非饱和渗透系数值位于4.3×10-9～5.6×10-7cm/s范围内(含水率区间为20 %～30 %)；ρd=1.55 g/cm3试样试验值位于4.1×10-9～1.7×10-7cm/s范围(含水率区间为25%～35%)。非饱和渗透系数值均远小于饱和渗透系数，且随含水率呈指数增长。

(3)利用van Genuchten和Fredlund等渗透系数模型对非饱和压实黄土渗透系数进行预测，得到完整的非饱和渗透系数曲线，基质吸力对渗透系数的影响很大。对比发现两模型在基质吸力较小时预测结果接近，但随基质吸力值变大误差也越来越大。对比瞬时剖面法计算结果，van Genuchten渗透系数模型预测结果的变化规律及数量级更接近实测值。