一种新的多址接入传输优化系统

周 鑫，周渊平，陈闽鄂，肖宇彤

（四川大学电子信息学院，四川成都 610065）

0 引 言

MIMO 系统由于其能提供分集增益和复用增益而被移动通信作为核心技术。面对日益增长的用户数据需求，马上就要到来的第五代移动通信必须实现高数据率、低时延的通信性能。传统MIMO 系统中，一根天线只能传输单个用户信号，若要提升数据传输率就必须增加天线数目。为了满足更大数据信息量的需求，5G 通信中必须要用到大规模天线阵列，即大规模MIMO 系统。在大规模MIMO 系统中，基站侧布置的天线数较传统MIMO 系统有一个数量级的提升，使用的天线数目越多，在空域能产生的自由度也更多，还能在不增加带宽的前提下提高数据传输率，并通过空间分集提高通信的可靠性[1-2]。

但仅仅通过增加天线数来提升数据传输率是不够的，传统认知单根天线只能传输一路用户信号限制了通信系统的发展，这种传输方式会造成硬件系统和射频链路的浪费。为求改进，一些新的多用户接入方式被提出。其中，最为新颖的是近些年提出的非正交多址接入（Non-orthogonal Multiple Access，NOMA）方式，NOMA 系统最大创新点就是在功率域复用多路用户，并且在接收端使用串行干扰消除（SIC）方法来解调出复用的多路信号，但这种方案经过实际验证，其信号解调复杂度较高，在如今的便携式设备上使用这种解调方式会存在很大的硬件资源开销，所以这种方案还需要进一步改进解调方式[3-4]。

基于现状，本文提出一种新的多址接入方式，其主要思想是单根天线能接入多路用户数据，与NOMA 系统不同的是，本文提出的多址接入方式对单个用户的加权系数可以根据接收端反馈回的误码率实时调整，而且接收端采用的是新型的MMSE+ML 混合检测方式。实验结果显示，这种新型的多址接入方式较传统NOMA 系统能在保持相同接入用户数目的情况下以较低复杂度解调出信号，并且在同等数据传输率的基础上还能保持较低的误码率。

1 系统模型

实验假设处在包含有一个M根天线的基站和N个单天线用户的小区内，系统框图如图1 所示。可以明显看出本文所提系统不同于常规MIMO 系统。

第一个不同之处是在发射端，可以从框图看出本文所提系统一根天线能复用Q路数据，第m根天线上叠加的Q路用户表示为sm=[sm1,sm2,…,smQ]T，则系统整体输入向量可表示为

第二个不同点在于每一个用户数据流都会与一个权值系数相乘，同样，可以将第m根天线上复用的用户smi的加权系数表示为wmi=Amiejθmi(m=1,2,…,M;i=1,2,…,Q)，其中，Ami和θmi分别表示加权系数的幅度与相位。则每根天线上加权系数组成的矩阵表示为wm=[wm1,wm2,…,wmQ]T，整个输入端的加权矩阵可写作w=

图1 本文所提系统模型Fig.1 Model of system proposed in the paper

第三个不同之处在于接收端的信号检测方法。普通的线性检测算法比如最小均方误差算法（MMSE）、迫零算法（ZF）等在本系统中不再适用，因为这些方法只能检测出单根天线上混合的Q路信号，而不能有效解调出所叠加的各路信号。最大似然检测方法（ML）理论上是可以解调出所有的用户信号，但这样做复杂度会极高，当传输信号采用QPSK 调制时，ML 要进行4M×Q次运算，在大规模MIMO 系统中M会是一个很大的数字，所以接收端不宜采用ML 检测算法。

为了能解调出混合的Q路信号，本文采用一种全新的MMSE+ML 混合检测算法，第一次MMSE 检测可得到混合的Q路用户数据，第二次ML 检测则把混合的Q路数据分离开来，这样做既能顺利解调出混合的各路信号，又能结合两种检测算法的优势从而极大地降低了解调复杂度。

第四个不同点就是框图中很明显的反馈部分，接收端将误码率反馈回发射端，发射端根据反馈回的误码率通过权值调整模块实时地调整各路信号所赋予的权值，最终使得整个通信系统有着最好的效果。

根据此框图，每根天线上所传输的混合信号可写为：

接收端收到的信号可表示为：

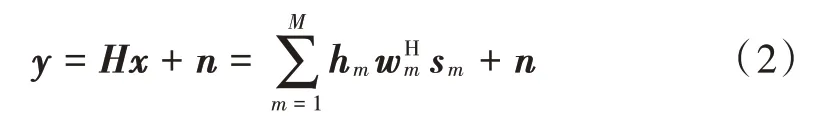
在信号检测部分，第一次MMSE 检测的均衡矩阵可写作：

则第一次MMSE 检测得到的混合信号可表示为：x′=GMMSEy，其中在第二次的ML 检测中，假设wm(m=1,2,…,M)已知，则第m个输入向量sm的估计值可表示为：

式（4）代表遍历所有星座集取值可能的组合，并选择其中与估计出的混合信号xm′ 误差最小的一组作为最终估计出的Q路信号。

从上面公式中可以看出原始用户数据的加权系数对判决结果是有影响的，实际上这些权值的作用就是减少各路数据的相关性，这样就更有利于信号的传输以及接收端对信号的判决，所以如何合理设置权值使各路信号相关性降到最低也是一个很重要的问题，本文采用权值优化模块得到使系统误码率最低的最优权值。

2 权值优化算法

权值优化的目的就是得到一组通信性能最好的权值，具体优化过程可简述为：算法首先设置若干个初始权向量，然后根据某些原则局部调整每一个权向量，然后分别计算每一个权向量应用到本文系统后在接收端解调后得到的误码率，根据此误码率再来更新、调整剩下的权向量，直到最后得到一个误码率最低的权向量，这就是所需要的最优权值。

差分进化算法是一种效率很高的最优解搜索算法，它在搜寻全局最优解上有着广泛的应用[5]。将其运用到本文提出的系统权值优化上，详细步骤可描述如下：

1）初始化相关变量。包括权值个体数量M，每个权值的维数D等，初始化所有权值个体[6]可表示为其中，参数i表示第i个权值个体，参数j表示权值个体的第j维，括号里面的系数表示种群迭代次数表示每个权值个体的每一维取值范围最小值和最大值；初始化方法为[7]：

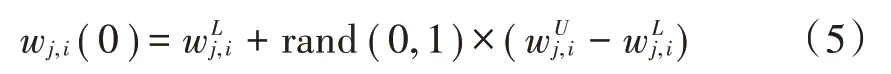
2）确定适应度函数。适应度指的是判断某个权值个体好坏与否的标准，用表示系统权值为wi(g)时经过检测算法得到的对原始信号xr的估计，用f(wi(g))表示第g代种群中第i个权值个体的误码率，并选用此函数作为适应度函数。

3）变异操作。对种群内所有个体进行差分策略的变异，具体方法是在所有权值个体中随机选取两个权向量，并取其差做缩放操作后作为第三个权向量的扰动值，以此得到个体wi(g)变异的中间体vi(g)：

式中：wa(g)表示当前种群中适应度最好的个体；α为缩放系数，本文实验均采用α=0.2。

4）交叉操作。随机选取vi(g)或原始个体wi(g)的第j维作为新个体ui(g)的第j维：

式中：CR 表示两个个体发生交叉的概率，本文实验此值设置为0.8；jrand取1～D之间的随机整数[8]。

5）选择操作。分别对第i个权值个体wi(g)与上一步经交叉后得到的ui(g)进行适应度计算，将适应度更好即误码率更小的留下来作为下一代的个体：

6）重复步骤3）～步骤5），直到迭代次数满足条件为止。

3 复杂度分析

由式（3）可知，MMSE 检测的复杂度为Ο(NM2+M3)，其中Ο(NM2)来自于矩阵的乘积，而复杂度Ο(M3)来自于对矩阵的求逆运算[9]。另外，还可从式（4）看出ML 检测的复杂度为Ο(MCQ)，所以本文所提的MMSE+ML 混合检测算法复杂度可写为Ο(NM2+M3+MCQ)，可以明显的看出MMSE+ML 混合检测算法复杂度很大程度上取决于Ο(MCQ)。在传统MIMO 系统中，若采用MMSE 检测，则其复杂度就为Ο(NM2+M3)，若要与本文系统保持同等的数据传输率，则必须将发射天线数目增加到Q×M，则其检测复杂度为Ο(NQ2M2+Q3M3)，采取系数表示在同等数据传输率基础上本文系统的信号检测复杂度与传统MIMO 信号检测复杂度的比值，若此值小于1 则表示本文系统复杂度更低。从复杂度表达式来看，若采用低价调制方式且天线数量达到一定程度时，本文的混合检测算法复杂度很可能会低于传统MIMO 系统信号检测的复杂度，所以这种混合检测算法有着很大的研究空间。

4 仿真结果分析

本文假设传输信道是慢衰落信道，且接收端对信道信息已知。输入信号采用QPSK 调制。图3，图4 中差分进化算法初始权值个体数量为30，仿真采样点数为10 000。

在保持数据传输率相等的情况下，本文系统和传统MIMO 系统信号检测复杂度的比值k随天线数目变化的曲线图如图2 所示。

由图2 可明显看出，每根天线复用路数大于等于Q=2 时，所有不同天线数目的复杂度比值都在1 以下，说明本文的混合检测算法复杂度比传统MIMO 系统检测算法复杂度更低。也可观测到当天线数目越多时，两者的比值越低，说明当天线数目越多时，本文系统的信号检测复杂度更能体现出它的优势，即本文系统很适合用在大规模MIMO 系统中。

在2×2 的系统中，分别采用传统MIMO 系统一根天线传1 路（Q=1）数据、NOMA 系统一根天线传2 路（Q=2）数据和本文系统一根天线传2 路（Q=2）数据，并将结果进行对比，仿真图如图3 所示。

图2 系统复杂度比值k 随天线数目变化图Fig.2 Variation of system complexity ratio k with quantity of antenna

图3 本文所提方案与NOMA 系统、传统MIMO 系统的比较Fig.3 Comparison of the proposed scheme with NOMA system and traditional MIMO system

由图3 可明显看出，随着信噪比的增大三条曲线的误码率下降趋势都很明显，但在相同收发天线数目的情况下，本文系统和NOMA 系统较传统MIMO 系统相比都能在提高数据传输率的基础上有着更低的误码率性能，且可分别获得2～5 dB，4～9 dB 的增益。特别地，还可看到在信噪比处于0～20 dB 时，本文系统比NOMA 系统在相同误码率情况下有着稳定的2 dB 以上的增益，说明本文方案采用的差分进化算法已经搜索到了全局最优权值向量，并取得了较好的效果。

图4 给出了本文系统在收发天线为1×2，一根天线叠加数据路数Q=2，3 时，与传统MIMO 系统收发天线为2×2，单根天线传输Q=1 路数据的对比。

可以看出本文系统在发射天线数目为1，每根天线叠加Q=2 路数据时，其效果仍然比发射天线数目为2，单根天线只叠加Q=1 路数据的传统MIMO 系统好，说明本文系统能在保持同等数据传输率基础上还能以更低的误码率解调出原信号，而且能减少一根天线的硬件消耗，这对于优化通信性能有着重大的意义。

同时也可看到本文系统在发射天线数目为1，每根天线叠加Q=3 路数据时，其效果仍好于拥有两根发射天线、单根天线传输Q=1 路数据的传统MIMO 系统，可以看到在同等误码率情况下，较传统MIMO 系统相比，本文系统能取得1～2.5 dB 的增益，即本文系统能在提高50%数据传输量的基础上有着更好的系统性能。

图4 本文所提方案Q=2，3 时与传统MIMO 系统的对比Fig.4 Comparison of the proposed scheme when Q=2 and 3 with traditional MIMO system

图5 比较的是本文系统在2 发2 收，SNR=8 dB 情况下，设置差分进化算法中的初始权值个体数量M分别为10，20，30 时，比较其寻找最优权值的收敛情况。

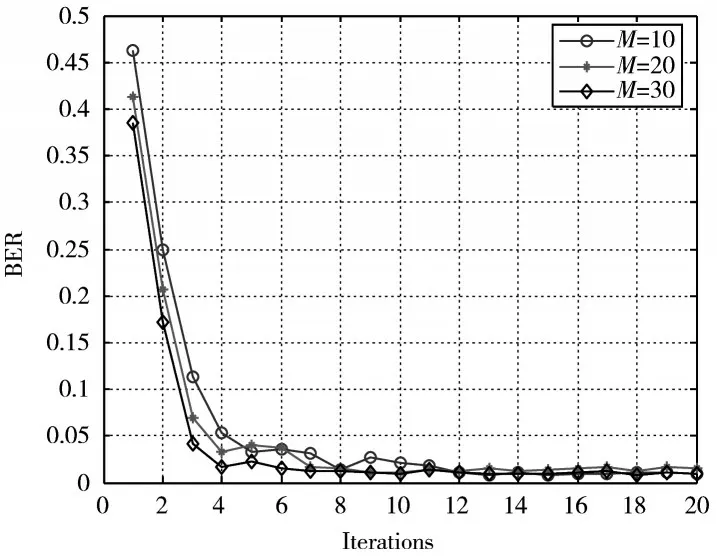
图5 种群个体数量不同时的收敛情况Fig.5 Convergence of populations at different number of individuals

从图5 可看出，当初始化权值个体数量M取10 时要循环13 次才能收敛；当M取20 时循环7 次就收敛了；当M取30 时收敛速度更快，只用了4 次就收敛了，说明初始化的种群个体数量对收敛速度还是有影响的。究其原因就是初始化时，权向量都是随机设置，有很大的不确定性，当初始化个体数量越多，随机设置的权向量与真正的全局最优权向量越接近的概率越大。所以如何设置初始化种群个体数量也是比较重要的，一个合适的M值能在保证收敛的情况下还能以最快速度找到最优权值，这对于系统程序的优化也是非常有意义的。

5 结 语

本文介绍的方案和NOMA 系统有点类似，但是和NOMA 系统也有着本质的不同，NOMA 系统单根天线也能接入多个用户，对每个用户数据也有加权（也就是功率），但NOMA 方案的加权系数是个实数，也就是只能调幅，在接收端根据这个实数进行串行干扰消除（SIC）以解调出信号，所以说NOMA 是在功率域区分用户[10]；而本文所提方案对每个用户加权系数为一个实数乘以一个复数，也就是既能调幅也能调相，这样能使信号间的相关性得到更灵活的调整，通过权值优化模块不断调整使其降到最低，在接收端也就能取得更好的误码率。可以将本文所提系统看作是NOMA 系统的扩展，仿真结果表明这种扩展理论上是成功的，在相同收发天线及数据传输率情况下，本文系统比NOMA 系统性能更好。不过本文只实验了传输数据采用QPSK 调制、且一根天线复用较少路用户数据的情况，所以接收端采用的ML 检测，如果复用用户数据路数更多或者采用高阶QAM 调制的话，用ML 检测也会提高检测的复杂度，所以寻找一种复杂度更低、适合高阶QAM 调制的检测算法也是一个比较重要的任务。