GNSS自适应双门限协同干扰检测算法

2019-12-09周思远杨婷婷吴玉成

现代电子技术 2019年23期

周平，周思远，杨婷婷，吴玉成

（1.扬州万方电子技术有限公司，江苏扬州 225006；2.重庆大学微电子与通信工程学院，重庆 400044）

0 引言

随着GNSS（Global Navigation Satellite System）在军、民等领域的应用越来越广泛，GNSS 无线电磁环境也越来越复杂，GNSS 面临着各种各样有意或者无意的干扰，这些干扰将影响导航系统对地面的监控以及用户的正常使用，对卫星导航的精度、可用性以及完整性等构成非常严重的威胁。到目前为止，为了抑制干扰信号对GNSS 接收机的影响，提高卫星导航通信的频谱利用率，关于GNSS 干扰监测与抗干扰技术[1]的研究越来越多。干扰检测作为干扰监测技术的基础，如何保证干扰检测的准确性和高效性对整个干扰监测系统具有重要意义。

现有的GNSS 干扰检测技术有很多，包括能量检测[2]、小波变换[3]、时频分析[4]以及循环平稳分析[5]等。其中，能量检测具有复杂度低、实现简单以及无需先验知识的优点，从实际应用出发，能量检测在GNSS 干扰检测领域得到了广泛的应用。

由于能量检测并不能区分主用户信号和噪声信号，在实际的GNSS 导航系统中具有不可预测性和时变性，导致认知节点无法准确地估计出噪声功率，故而能量检测的检测性能受噪声不确定性的影响很大。文献[6-7]研究了噪声不确定性下信号检测问题，研究表明，在给定噪声不确定度的条件下，当信噪比低于某门限值时，能量检测性能严重恶化。

目前用于抑制噪声不确定性影响的方法主要包括双门限检测、协作检测、联合检测、自适应频谱检测以及利用与噪声无关的特征进行检测等。

文献[8]研究了认知无线电噪声不确定条件下的频谱感知技术，采用双门限协作检测算法，门限值根据各节点的噪声不确定度设置，仿真表明在各节点噪声不确定度不同的条件下，拥有良好的检测性能。文献[9]提出一种将双门限检测和循环平稳检测相结合的检测算法，不仅在噪声不确定条件下拥有良好的检测性能，而且计算复杂度低于循环平稳检测。文献[10]根据随机矩阵原理，通过信号协方差矩阵最大最小特征之比进行认知无线电信号检测，此算法不仅不需要信号先验信息，而且能克服噪声不确定性的影响，仿真通过ATSC DTV 信号验证了算法的可行性。上述方法虽然可以抑制噪声不确定性的影响，但是文献[8-9]需要知道各节点噪声不确定度的大小，而文献[10]的计算复杂度较高。

本文采用双门限协作检测来抑制环境噪声对干扰检测的影响。在噪声不确定度未知的情况下，噪声不确定系数的设置对检测性能影响很大，较大的噪声不确定系数会使计算复杂度增加，而较小的噪声不确定系数会降低检测概率。基于此，本文提出一种基于自适应门限的双门限协同干扰检测算法，在噪声不确定度未知的情况下，通过噪声环境的变化自适应地调整噪声不确定系数，不仅可以在信道环境较差时保持较好的检测性能，而且可以在信道环境较好时降低计算复杂度。

1 能量检测模型

能量检测的思想是在一定时间内求能量累积值，把检测出来的能量值与阈值进行比较，从而判断干扰信号的有无。为了能够有效地测量出接收信号的能量值，首先将接收信号经过带通滤波器进行滤波，再经过一个A/D 转换器，把模拟信号转换为数字信号，然后对离散信号进行平方、累加平均运算，最后将检测统计量送入门限判决器与门限值比较并做出判决。

不含干扰信号与含干扰信号问题可表示为：

式中：x(t)为GNSS 接收信号；j(t)为干扰信号；n(t)为噪声信号。n(t)和j(t)之间相互独立。

在高斯白噪声环境下对干扰信号进行检测，由文献[11]可知，检测统计量近似服从高斯分布：

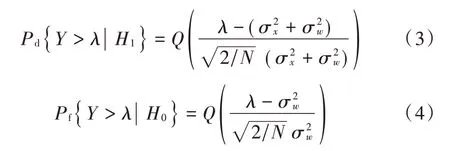
进一步可得到检测概率为：

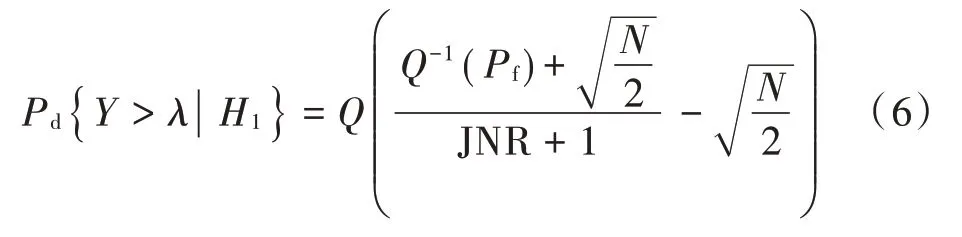
2 双门限协作干扰检测

通常情况下，都是假设接收信号的噪声功率为一确定值。但是，在真实的电磁环境中，还存在一些未知的干扰或者噪声信号对噪声功率产生影响，使得噪声功率会随环境和时间的变化而变化，这就是噪声不确定性。由于噪声不确定性的影响，能量检测值会在一定范围内浮动，导致检测概率降低以及虚警概率加大，对检测性能造成严重的影响。因此，为了降低噪声不确定性对检测性能的影响，采用双门限协作干扰检测。

2.1 噪声不确定下的双门限检测

定义一个噪声不确定区间，即：

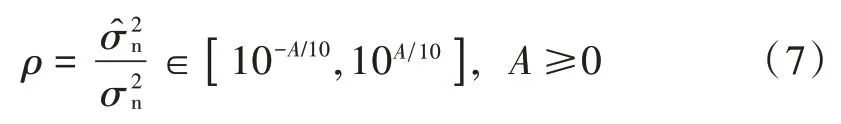
由噪声不确定系数ρ和虚警概率，双门限值可以表示为[12]：

如图1 所示，设定两个检测门限将整个检测区域分为3 个部分，当检测统计量处于不确定空间（λ1和λ2之间）之外时，将直接采用硬判决，发送本地判决结果给融合中心，若检测统计量大于λ2，则判决为H1，若检测统计量小于λ1，则判决为H0。

图1 双门限判决示意图Fig.1 Schematic diagram of dual-threshold decision

当检测统计量处于不确定空间时，将不确定空间的信息发送至融合中心进行软合并判决，判决标准如下：

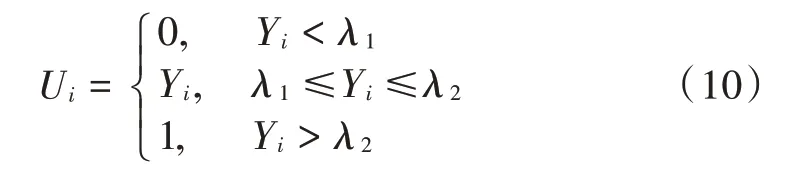
式中：Ui是第i个用户的判决结果；Yi是第i个用户的检测统计量。采用软判决可以减小干扰检测误检概率，提高判决的可靠性，当ρ=1 时，λ2=λ1，此时采用单门限判决，当ρ＞1 时采用双门限软判决。

2.2 基于可信度的加权协同双门限检测

在实际环境中，单节点判决容易受到衰落、多径等因素的影响，导致检测性能不理想，而协作频谱感知可以有效解决此问题。

由于各节点的噪声环境与可信度存在差异，仅对各节点的判决结果进行逻辑操作或者直接累加，并不能得到较好的检测性能。为了体现对各节点的偏好情况，使中心节点的数据融合更偏向于噪声环境较好的节点，等权重的融合方案并不适用复杂的环境。基于此，采用基于信任度的合并方式在数据融合方面得到了广泛的应用，将影响检测准确度的因素作为融合权重，使中心节点在数据融合时偏向噪声环境好的节点，从而使得检测准确度更高。

假设N个节点检测到的噪声功率为pni，i=1,2,…,N，接收信号功率为pri，则每个本地节点的信道环境信息可近似表示为：

权重ωi可表示为：

假设融合中心的数据为Ri，收到的两类数据为：

式中：Xi是本地节点硬判决之后的数据；Yi是发送给融合中心的软数据，即第i个用户的检测统计量。融合中心再次判决之后的数据为D，即：

通过双门限协同检测之后的检测概率与虚警概率分别为：

式中Pd与Pf为全局检测概率与虚警概率，可以看出协作检测比较关键的是获得噪声功率pni，接下来将会介绍如何有效地估计出噪声功率。

本文采用通过滑动窗口滤波寻找保护频带的方法求得噪声功率[13]，首先对接收到的信号进行滑动滤波，求出功率值，如果低于预设阈值，则判定为保护频带，基本框图如图2 所示。

图2 滑动窗口滤波器寻找保护频带结构框图Fig.2 Structure block diagram of sliding window filter for guard band

接收信号x(t)首先进行抽样处理得到数字信号，再进行N点FFT 变换得到局部频谱，频域抽样之后的信号x(k)可以表示为：

功率值p(k)可以通过样点频率x(k)的平方获得：

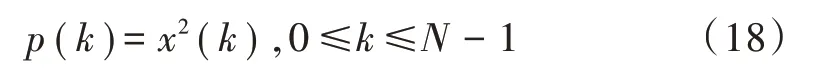
其中，滑动窗处理的算法可以表示为：利用滑动窗计算所有频点的平均功率值，直到将所有样点数据处理完毕为止。第k路滑窗函数ω(k)可以表示为：

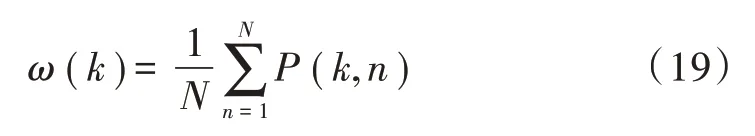
通过上述方法可以快速找到保护频带，在保护频带内基本只有噪声而没有其他信号，此时只要检测该频段内的噪声功率便可得到所需的噪声功率。

3 自适应双门限协同干扰检测

双门限值的设置对干扰检测精度的影响很大，而门限值的设定与噪声不确定系数ρ有关，设置ρ的大小对检测结果有很大的影响。本节主要研究噪声不确定系数ρ随着噪声环境的变化而自适应调整的一种方案。在信道环境差的情况下，增大ρ值，提高检测精度，而当信道环境较好的时候，减少ρ值，可以降低检测算法复杂度，当达到某一设定的噪声环境时，ρ=1，此时由双门限检测变为单门限检测。

噪声不确定系数ρ的取值如图3 所示。

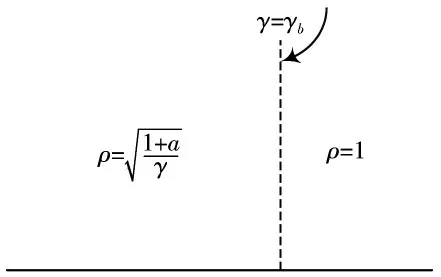
图3 噪声不确定度自适应设置Fig.3 Self-adaptive setting of noise uncertainty

自适应双门限协同检测算法的具体步骤说明如下：

1）通过检测保护频带得到每个节点的信道状态信息γ。

2）设定信道状态的门限值为γb，噪声不确定度的上限值设为ρλ，此值应根据实际测试设置。

3）当信道环境信息γ≥γb时，此时的信道环境较好，将噪声不确定系数ρ设为1。当γ＜γb时，根据下面的公式自适应调整噪声不确定系数：

式中：a为调整因子，但是ρ值并不是一直增加，当ρ=ρλ时，此时由于增加噪声不确定系数对性能增益不明显，即当γ继续变小时，将ρ设为固定值ρλ。

4）确定噪声不确定系数ρ之后，通过式（8）和式（9）计算上下门限值。

5）当确定好双门限值之后，对每个节点进行双门限准则判决，将每个节点的判决结果送入到融合中心，当融合中心收到的硬判决结果中有一个节点的判决结果为1 时，此时将不再对融合中心进行操作，直接判定干扰信号存在；否则，则对融合中心接收到的软信息采用基于可信度合并方法进行数据合并，设置合适的判决门限值，当合并后的信息大于门限值，则干扰信号存在，否则干扰信号不存在。

4 仿真结果及分析

将每个节点的噪声环境设成不同，依次仿真了采用“或”融合准则、等增益合并、最大比合并的检测性能随着虚警概率不断变化的曲线。其中，最大比合并采用基于可信度的加权协同检测，平均干噪比设为-18 dB，噪声不确定系数设为4，虚警概率为0.1，采样点数N=4 096，最大不确定度A=7，如图4 所示。

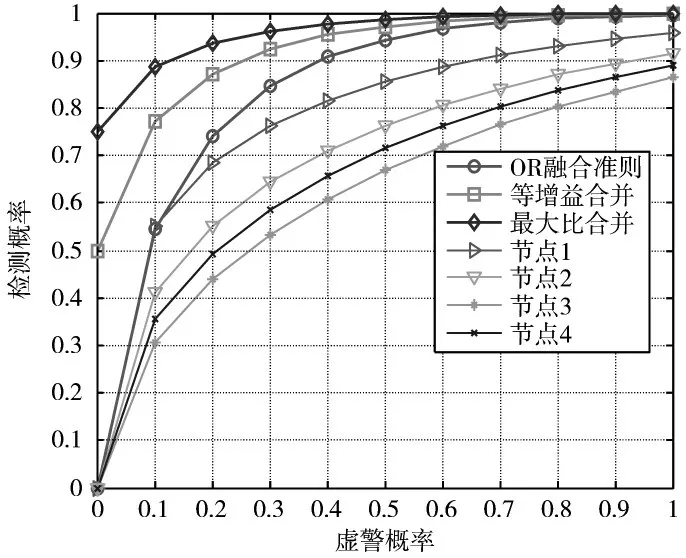
图4 不同融合准则的检测性能Fig.4 Detection performance at various fusion criteria

由图4 可以看出：“或”融合准则虽然可以在一定程度上提高检测性能，但是在单个用户的检测概率较低的情况下，“或”融合准则提升性能不大，等增益合并较“或”准则在低检测概率下有不小的性能提升，最大比合并性能最佳。理由是因为硬判决“或”合并是将本地信息进行判决之后再传递给融合中心，这样使得融合中心丢失了很多信息，所以性能较差，而等增益合并虽然是将各节点的信息传回了融合中心，但是没有利用任何先验信息，给每个节点的信任度相同，故而其性能比“或”准则好，比最大比合并较差，最大比合并估计出了每个节点的噪声环境信息，在融合中心进行判决时偏向于信道环境较好的节点，故而其性能最佳。

当采用基于可信度的加权协作干扰检测时，噪声不确定系数ρ的不同也会给检测性能造成较大的影响，图5 给出了在不同ρ值下的ROC 曲线。

图5 不同ρ 值的检测性能Fig.5 Detection performance at various ρ values

由图5 可以看出，随着ρ值不断增大，检测性能也会随之变好，但是当ρ的取值超过4 之后，性能增益不明显，再继续增大ρ值，只会增加计算复杂度，因此可以设定ρ的门限值ρλ为5。

由于实际GNSS 信号很微弱，已经完全淹没在噪声之中，可以把GNSS 信号当做噪声处理，只考虑干扰信号对干扰检测的影响，干扰信号选择脉冲干扰。仿真环境为高斯白噪声，加入具有不确定性的白噪声，最大不确定度A=7。

当设置不同的调整因子a值，以及不同的门限值γb时，基于门限自适应的双门限协同检测算法在低干噪比下的性能曲线如下：

预设γb=0.5，虚警概率设为0.1，用户数为4，采样点数N=4 096，当干噪比不断变化时，调整因子a的取值对检测性能的影响如图6 所示。

图6 不同a 值下的检测概率随干噪比变化曲线Fig.6 Variation of detection probability with JNR at various a values

预设γb=0.5，平均干噪比设为-18 dB，用户数为4，采样点数N=4 096，当虚警概率不断变化时，调整因子a的取值对检测性能的影响如图7 所示。

图7 不同a 值下的检测概率随虚警概率变化曲线Fig.7 Variation of detection probability with pfa at various a values

当调整因子设为0.5，虚警概率设为0.1，用户数为4，采样点数N=4 096，干噪比不断变化时，门限值γb对检测性能的影响如图8 所示。

当调整因子设为0.5，平均干噪比设为-18 dB，用户数为4，采样点数N=4 096，虚警概率不断变化时，门限值γb对检测性能的影响如图9 所示。

如图6～图9 所示，随着调整因子变大或者门限值γb越大，检测性能越好，当干噪比大于-14 dB 时，可以保持检测概率在0.95 以上，检测性能较好，满足在GNSS低干噪比下对压制式干扰的检测。

图8 不同噪声门限值下的检测概率随干噪比变化曲线Fig.8 Variation of detection probability with JNR at various noise threshold values

图9 不同噪声门限值下的检测概率随虚警概率变化曲线Fig.9 Variation of detection probability with pfa at various noise threshold values

门限值γb的设置对检测性能和计算复杂度影响较大，若γb设置太大，此时性能提升较小，而且也会相应地增多送入融合中心的软信息数据，增大花销；若γb设置太小，检测性能较差，应该根据实际需求设置门限值γb大小。调整因子主要是对噪声不确定系数进行微调，当γb确定之后，若得到的检测性能不满足要求，则可以增大调整因子，若此时检测性能比需求的要好，则可以相应降低调整因子以相应降低噪声不确定系数，从而降低复杂度。